§ 4.2. Собственная масса замкнутой системы заряженных частиц и полей

Замкнутая система заряженных частиц и полей – это такая система, которая поддерживает свое устойчивое состояние за счет внутренних сил. Согласно теореме Ирншоу, эта система должна состоять из движущихся заряженных частиц, которые взаимодействуют между собой посредством электромагнитных полей, создаваемых заряды этих частиц. Так как частицы движутся, они создают не только кулоновские электромагнитные поля, а также электромагнитные поля в виде электромагнитных волн, которые уходят на бесконечность. Причем, потери энергии (см. (3.11.7)):

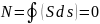
Будем считать потери энергии незначительными.

Для замкнутой системы имеем закон сохранения энергии

где 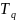– сумма энергий отдельных частиц; и закон сохранения импульса

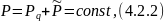
где

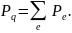
Здесь

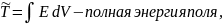
а (см. (3.12.16))

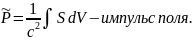
Оба закона можно объединить в один закон сохранения энергии-импульса, если ввести четырехмерный вектор импульса замкнутой системы:

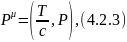
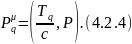
Как мы уже знаем, произведение четырехмерных векторов образует инвариант

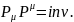
Определим собственную массу замкнутой системы согласно соотношению

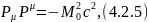
а с другой стороны с учетом (4.2.2)-(4.4.4)

Приравнивая (4.2.5) и (4.2.6) получим выражение для собственной массы замкнутой системы:

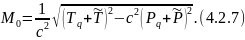
Т.к. эта величина является инвариантом, то проще всего ее вычислять в системе покоя. Для простоты рассмотрим систему, состоящую из одного заряда и кулоновского поля, которое он создает. Тогда для покоящегося электрона получим, что импульс

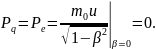
Полевой импульс также равен нулю, т. к. магнитное поле покоившегося заряда отсутствует:

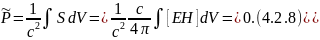
Тогда для собственной массы системы получим

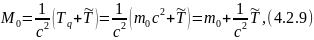
где энергия частицы

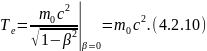
Полная энергия поля в системе покоя выглядит следующим образом:

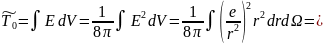
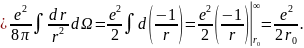
Подставляя выражение для энергии в выражение для собственной массы системы, получим

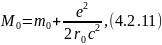
где – масса “голого” электрона, а 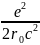– масса электромагнитной “шубы” или электромагнитная масса электрона.

Если 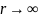(частицы точечные), то собственная масса стремится к бесконечности, а этого не может быть. В связи с этим, принято считать, что классический радиус электрона равен

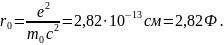
Будем считать, что экспериментально наблюдаемой массой электрона является

Рассмотрим случай замкнутой системы многих заряженных частиц вместе с полями, которые они создают. Такая система устойчивым образом может существовать только тогда, когда частицы движутся. Не существует устойчивых систем заряженных частиц, находящихся в покое (теорема Ирншоу). Следовательно, будем предполагать, что заряды движутся, но в релятивистском приближении (с небольшими скоростями), поэтому в этом случае магнитное поле отсутствует, т.к. оно ~ . При этом полный импульс системы равен нулю.

Тогда собственная масса системы

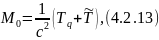
где энергия частиц равна

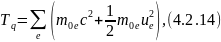
а полная энергия поля

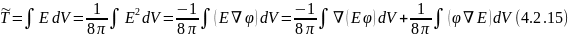
Используя теорему Остроградского-Гаусса, получим

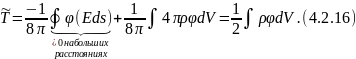
Т.к. плотность заряда

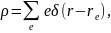
то

Здесь

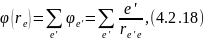
а 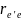– расстояние от заряда до заряда. Используя данный факт, запишем энергию

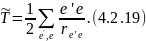
Это выражение совпадает с потенциальной энергией системы зарядов (4.1.1):

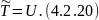
Тогда собственная масса такой системы примет вид

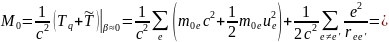
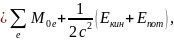
где

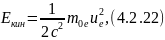
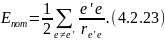
Энергия такой системы больше энергии покоя составляющих ее частиц за счет кинетической энергии и потенциальной энергий взаимодействия частиц: