Введение

Электродинамика – раздел физики, в котором изучается взаимодействия между электрически заряженными телами.

Электрические и магнитные поля могут существовать и независимо от заряда в виде самоподдерживающихся переменных во времени комбинаций, в этом случае они называются электромагнитными волнами.

Важность изучаемого предмета состоит в том, что окружающая природа буквально насыщена электричеством и магнетизмом.

Методы изучения электродинамики:

1. Индуктивный метод («от простого к сложному»): на основе сделанных обобщений формулируются законы.

2. Дедуктивный метод: сначала выдвигаются общие предположения, исходя из которых затем формулируются и уравнения движения, и законы электродинамики;

Дедуктивный метод позволяет значительно сэкономить время.

Глава I математический аппарат и основные понятия классической электродинамики

§ 1.1. Постулаты специальной теории относительности

Математической основой электродинамики является специальная теория относительности. Основными понятиями СТО является пространство и время. Пространство необходимо для того, чтобы указать место, где произошло событие, а время указывает на тот момент, когда произошло это событие.

СТО внесла коренные изменения в свойства пространства и времени. Ранее они рассматривались независимо друг от друга, при этом наше трехмерное пространство считалось однородным и изотропным. Время отсчитывалось по абсолютным часам, которые шли одинаково во всех точках трехмерного пространства. После создания СТО свойства однородности и изотропности пространства были перенесены на четырехмерное пространство, в котором имеется три пространственных оси (x, y,z) и одна временная ось. Напомним, что пространство называется однородным, если все его области равнозначны, а значит, преобразование параллельного переноса переводит пространство в само себя. Изотропность пространства означает, что все направления в нем равноправны, и уже поворот относительно любой оси переводит систему в эквивалентное состояние. При этом по-прежнему все эти оси считаются взаимно перпендикулярными.

Эти свойства необходимы для того, чтобы выполнялись уравнения движения, законы сохранения (энергии, импульса и т. д.). С однородностью пространства связан закон сохранения импульса, а с изотропностью – закон сохранения момента импульса.

Важнейшими объектами изучения в электродинамике являются заряженные частицы и поля. При этом мы будем вначале рассматривать точечные частицы, для которых размеры и формы не влияют на характер движения. Взаимодействия между зарядами передаются электрическими и магнитными полями. Если бы кроме электрических существовали магнитные заряды, тогда покоящийся магнитный заряд порождал бы магнитные поля и для него электрическое поле равнялось нулю. Но если бы этот заряд пришел в движение, то, как показывают расчеты на основе СТО, при этом создалось бы и электрическое поле.

СТО разрешила спор о том, как передаются взаимодействия между частицами. Как известно, существуют две теории: теория дальнодействия (взаимодействия передаются мгновенно) и теория близкодействия (взаимодействия передаются не сразу, а от точки к точке).

Покажем, что механика Ньютона является в действительности теорией дальнодействия. Действительно, вектор силы f согласно Ньютону связан с потенциальной энергией U соотношением

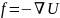
(1.1.1)

где 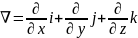- вектор набла.

Из (1.1) вытекает, что теория Ньютона является теорией дальнодействия. Рассмотрим этот вопрос более подробно. В случае точечного заряда будем иметь:

U=eφ(r), (1.1.2)

где φ-скалярный потенциал точечного заряда, равный

e e Рис.1

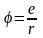. (1.1.3)

Подставим полученное выражение в формулу (1.1):

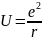(1.1.4)

Теперь можно найти силу f:

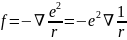, (1.1.5)

где .

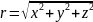
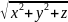Тогда:

.

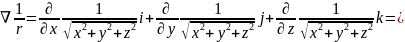
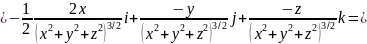
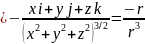Таким образом,

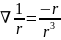(1.1.6)

Отсюда следует, что 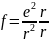(1.1.7)

Уравнение (1.1.7) предполагает, что если один из зарядов вышел из состояния равновесия, то второй заряд в тот же самый момент тоже выйдет из состояния равновесия, следовательно, скорость передачи взаимодействия будет равна ∞. Таким образом, механика Ньютона является теорией дальнодействия. В теории близкодействия взаимодействие передается от точки к точке с конечной скоростью. Эта теория более материалистична.

В результате многочисленных экспериментов было установлено, что скорость распространения взаимодействия является конечной и равной скорости света: с=299,792, 458 км/с ≈ 3^.10¹⁰ см/с. Это обстоятельство легло в основу СТО, построенной Эйнштейном.

Сформулируем постулаты Эйнштейна:

1. скорость света одинакова во всех инерциальных системах отсчета и не зависит от скорости движения источника света;

2. во всех инерциальных системах отсчета все законы природы действуют одинаково.

Можно сформулировать выводы из этих постулатов:

1. абсолютно твердых тел в природе не существует

Рис.2

Под твердым телом будем понимать тело, в котором расстояние между любыми двумя точками 1 и 2 остается постоянным (рис.2).

2. время не является абсолютным, т. е. оно не течет одинаково во всех инерциальных системах отсчета

x,x′ Рис.3

Последнее обстоятельство поясняется на рис.3. Из рисунка видно, что

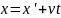
y=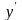

Это хорошо известные нам преобразования Галилея для координат.

Если точка не покоится, а движется, то чтобы найти ее скорость u нужно взять производную по t:

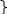
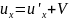X

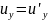
Если считать, что частица движется со скоростью света вдоль оси ОХ, то получаем

c=c+v.

Где ошибка? Очевидно, это связано с тем, что мы предполагали, что в штрихованной системе и в нештрихованной время течет одинаково, т. е. является абсолютным.

3. Скорость любой материальной частицы не может превышать скорость света.

Этот факт находит убедительное подтверждение. Предположим противное. Тогда мы можем передавать взаимодействия между такими частицами со скоростями большими скорости света. А это противоречит постулату Эйнштейна.

СТО является основой новой механики, отличной от механики Ньютона. Она называется релятивистской механикой, а частицы, которые летят со скоростью, близкой к скорости света, называются релятивистскими частицами.

Как сопоставить законы релятивистской механики с законами механики Ньютона?!

Релятивистская механика является обобщением механики Ньютона на случай движения частиц с релятивистскими скоростями. Поэтому, если скорость частицы U<<c, то можно пользоваться механикой Ньютона.

В макроскопической физике действует механика Ньютона, а в микрофизике – релятивистская механика. Эта ситуация отражает принцип соответствия в физике (всякая новая теория в каких-то областях должна совпадать с хорошо известной и проверенной теорией).