
I семестр
Понятие множества.
Постоянные и переменные величины. Определение функции. Область определения функции. Способы задания.
Понятие функции. Основные свойства функции
Элементарные функции. Классификация функций. Преобразование графиков.
Числовые последовательности. Классификация последовательностей
Предел числовой последовательности. Основные теоремы о пределах последовательности.
Предел функции в точке. Односторонние пределы функции в точке.
Бесконечно большие и бесконечно малые величины. Связь между бесконечно малыми и бесконечно большими величинами.
Предел функции в бесконечности.
Основные теоремы о пределах функции.
Первые и второй замечательные пределы.
Раскрытие неопределенностей вида 0/0, ∞/∞, 0*∞, ∞-∞,00,1∞,∞0.
Непрерывность функции в точке и на интервале. Точки разрыва функции.
Комплексные числа Исходные определения. Геометрическое изображение комплексных чисел. Комплексная плоскость.
Основные действия над комплексными числами.
Возведение комплексного числа в степень.
Извлечение корня из комплексного числа.
Показательная и тригонометрическая формы комплексного числа.
Задачи, приводящие к понятию производной. Производная функции: ее геометрический и механический смысл.
Производная сложной функции. Производная обратной функции. Производная функции, заданной неявно.
Производная степенно-показательной функции. Производная функции заданной параметрически.
Производные высших порядков. Механический смысл производной второго порядка.
Дифференциал функции: его геометрический смысл.
Основные теоремы дифференциального исчисления (теорема Ферма).
Основные теоремы дифференциального исчисления (теорема Ролля).
Основные теоремы дифференциального исчисления (теорема Лагранжа).
Правило Лопиталя (применение производной к вычислению пределов).
Возрастание и убывание функций. Экстремумы функций
Наибольшее и наименьшее значение функции на отрезке.
Выпуклость функции. Точки перегиба.
Асимптоты графика функции.
Общая схема исследования функций и построения их графиков.
Множества в п-мерном пространстве.
Функции нескольких переменных. Геометрическое изображение функции двух переменных.
Предел и непрерывность функции нескольких переменных. Свойства непрерывных функций.
Дифференцируемость функции нескольких переменных.
Частные производные функции нескольких переменных.
Дифференциал функции нескольких переменных.
Дифференцирование неявных и сложных функций.
Производная по направлению Градиент.
Частные производные и дифференциалы высших порядков.
Экстремумы функции двух переменных.
Наибольшее и наименьшее значение функции нескольких переменных.
II семестр
Неопределенный интеграл, его свойства.
Таблица основных интегралов.
Интегрирование заменой переменной.
Интегрирование по частям.
Интегрирование рациональных дробей.
Интегрирование тригонометрических функций:

Интегрирование некоторых видов иррациональностей:
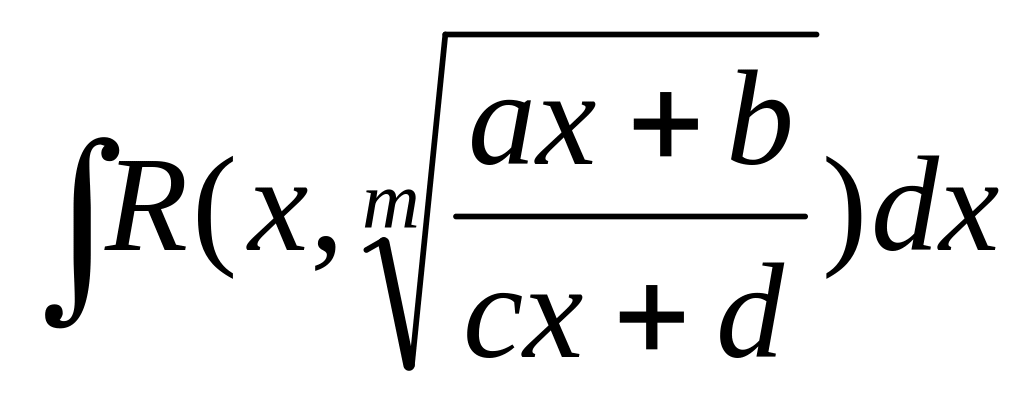 ,
,
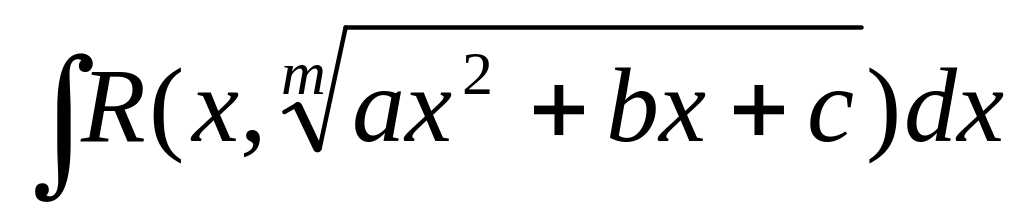
Определенный интеграл, его свойства. Криволинейная трапеция.
Формула Ньютона – Лейбница.
Вычисление определенных интегралов способом подстановки и по частям.
Приближенное вычисление определенных интегралов.
Геометрические приложения определенного интеграла: вычисление площадей фигур, объемов тел.
Несобственные интегралы с бесконечными пределами интегрирования.
Несобственные интегралы от неограниченных функций.
Несобственные интегралы от разрывных функций.
Дифференциальные уравнения (общие понятия). Задачи, приводящие к дифференциальным уравнениям.
Дифференциальные уравнения первого порядка (общие понятия). Изоклины.
Теорема существования и единственности решения задачи Коши.
Задачи Коши.
Дифференциальные уравнения с разделяющимися и разделенными переменными.
Однородные дифференциальные уравнения первого порядка.
Дифференциальные уравнения, приводящиеся к однородным.
Линейные дифференциальные уравнения первого порядка.
Уравнение Бернулли.
Дифференциальные уравнения высших порядков (общие понятия). Задача Коши.
Понятия о краевых задачах для дифференциальных уравнений. Уравнения, допускающие понижение порядка.
Теорема о существовании и единственности решения дифференциального уравнения п-го порядка.
Дифференциальные уравнения вида у(п)= f(x).
Дифференциальные уравнения второго порядка, приводимые к уравнения первого порядка.
Однородные линейные уравнения (определения и общие свойства).
Однородные линейные уравнения второго порядка с постоянными коэффициентами.
Неоднородные линейные уравнения второго порядка с постоянными коэффициентами.
Понятие числового ряда. Сумма ряда, частичная сумма, остаток ряда,
Сходимость и расходимость числового ряда.
Необходимые условия сходимости. Свойства сходящих рядов.
Признаки сравнения рядов. Эталонные ряды.
Ряды с положительными членами. Признак Даламбера и Коши.
Интегральный признак Коши - Маклорена.
Знакочередующиеся ряды. Признак Лейбница.
Абсолютная и условная сходимость.
Ряды с комплексными членами.
Функциональные ряды. Степенные ряды. Теорема Абеля.
Радиус сходимости. Интервал сходимости. Область сходимости.
Приложение степенных рядов к приближенным вычислениям.
Ряды Тейлора и Маклорена.
Разложение в степенной ряд элементарных функций.
|
Основная литература
|
1 |
Бугров, Я.С. Высшая математика. Дифференциальные уравнения. Кратные интегралы. Ряды. Функция комплексного переменного./ Я.С. Бугров, С.М. Никольский.-6-е изд., стереотип. -М.: Дрофа, 2004 (Высшее образование. Современный учебник) |
2 |
Высшая математика для экономистов / Под ред. Н.Ш. Кремера .- 2-е изд., перераб. и доп.. - М. : ЮНИТИ, 2007. - 471 с - ISBN 5-238-00030-8. (Золотой фонд Российских учебников) |
3 |
Высшая математика для экономистов /Под ред. Н.Ш. Кремера, -2-е изд., перераб. и доп. –М.: ЮНИТИ, 2002 МО РФ |
4 |
Ильин, В.А. Высшая математика [ Текст] : учебник В.А. Ильин, А.В. Куркина. 3-е изд. перераб. и доп. –М.: Проспект, 2009 (Классический университетский учебник) |
5 |
Высшая математика для экономистов / Под ред. Н.Ш. Кремера .- 3-е изд. - М. : ЮНИТИ, 2007. - 479 с. - (Золотой фонд Российских учебников) - ISBN 5-238-00991-7. |
6 |
Красс, М.С. Математика для экономических специальностей. Уч. пособие / М.С. Красс. –М.: Дело, 2002 МО РФ |
7 |
Красс, М.С. Математика в экономике. Основы математики / М.С. Красс . - М. : ФБК-ПРЕСС, 2008. - 472 с - ISBN 5-88103-160-1. |
8 |
Красс, М.С. Математика для экономического бакалавриата. Учебник / М.С. Красс, Б.П. Чупрынов. –М.: Дело, 2005 |
9 |
Красс, М.С. Математика в экономике. Основы математики. / М.С. Красс –М.: ФБК, -Пресс 2005 |
10 |
Макаров, С.И. Математика для экономистов. Уч. пособие / Макаров С.И. –Самара: Изд-во Самарской гос. Эконом. Академии. 2002 |
11 |
Натансон, И.П. Краткий курс высшей математики / И.П. Натансон, -8-е изд., стереотип. СПб.: Лань, 2005 |
12 |
Натансон, И.П. Краткий курс высшей математики / И.П. Натансон, -4-е изд., стереотип. СПб.: Лань, 2001 |
13 |
Солодовников, А.С. Математика в экономике: учеб.для вузов / А.С. Солодовников, В.А. Бабайцев, А.В. Браилов . - М. : Финансы и статистика, 1998. - 224с - ISBN 5-279-01943-7. |
14 |
Осипова, В.А. Основы дискретной математики: уч. пособ./ В.А. Осипова. –М.: ИНФРА, 2006 |
15 |
Плис, А.И. MathCAD. Математический практикум для инженеров и экономистов: уч. пособ./ А.И. Плис, Н.А. Сливина 2-е изд. доп. И перераб. – М.: Финансы и статистика, 2003 |
16 |
Самаров, К.А. Финансовая математика. Практический курс: уч. пособ./ К.А. Самаров. –М.: Альфа –М.:ИНФРА-М, 2006 |
17 |
Фадеев, Д.К. Задачи по высшей математике./ Д.К. Фадеев, И.С. Соминский 15-е изд. стереитип.-СПб.: Лань, 2005 |
19 |
Шипачев, В.С. Высшая математика: уч.пособ./ В.С. Шипачев.-6-е изд., стереотип. – М.: Высшая школа, 2003 |
|
Дополнительная литература |
19 |
Акулич, И.Л. Математическое программирование в примерах и задачах: учеб. пособие / И.Л. Акулич .- 2-е изд., испр. - CПб. : Лань, 2009. - 347 с. - Библиогр.: с. 346-347. - ISBN 978-5-8114-0916-7. |
20 |
Гашков, С.Б. Арифметика. Алгоритмы. Сложность вычислений: уч. пособие/ С.Б. Гашков, В.Н. Чубариков,-2-е изд., перераб. – М.: Высшая школа 2000 |
21 |
Замков, О.О. Математические методы в экономике: Учебник / О.О. Замков, А.В. Толстопятенко, Ю.Н. Черемных ; Под ред. А.В. Сидоровича.- 3-е изд. , перераб. - М. : Дело и сервис, 2001. - 368с. - (Учебники МГУ им. М.В. Ломоносова) - ISBN 5-86509-054-2. |
22 |
Коршунова, Н.И. Математика в экономике: учеб. пособ / Н.И. Коршунова, В.С. Плясунов . - М. : Вита-Пресс, 1996. - 368с - ISBN 5-7755-0012-1. |
23 |
Экономико-математическое моделирование: учебник / Под ред. И.Н. Дрогобыцкого . - М. : ЭКЗАМЕН, 2006. - 798 с - ISBN 5-472-01573-1. |
24 |
Пантелеев, А.В. Методы оптимизации в примерах и задачах / А.В. Пантелеев, Т.А. Летова . - М. : Высшая школа, 2002. - 544с - ISBN 5-06-004137-9. |
25 |
Плис, А.И. Mathcad. Математический практикум для инженеров и экономистов: Учеб. пособие / А.И. Плис, Н.А. Сливина .- 2-е изд., доп. и перераб. - М. : Финансы и статистика, 2003. - 656 с. : ил. - ISBN 5-279-02550-Х.7 Учебно-методическое обеспечение дисциплины (модуля) |
26 |
Математика в экономике: учеб.для вузов / А.С. Солодовников, В.А. Бабайцев, А.В. Браилов,И.Г. Шандра . - М. : Финансы и статистика, 1999. - 376с - ISBN 5-279-01944-5. |
27 |
Лабскер, Л.Г. Игровые методы в управлении экономикой и бизнесом: уч. пособ./ Л.Г. Лабскер, Л.О. Бабешко. –М.: Дело, 2001 |
28 |
Большой справочник по математике. -М.: АСТ, Астрель, Олимп, 2000 |
|
Интернет-ресурсы
|
