2. Первая вкладка

Первая вкладка – «Состав порошковой смеси». Здесь содержатся поля для ввода начальных условий, выбор распределения, по которому будет производиться расчет, график данного распределения и данные, полученные в результате генерации. Выбор распределения осуществляется с помощью компонента ComboBox, в котором содержатся названия распределений. Для каждого распределения необходимо задать начальные условия.

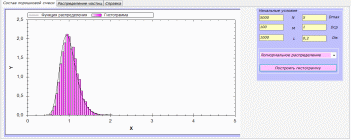
Рисунок 4. Первая вкладка «Состав порошковой смеси»

После ввода начальных условий необходимо нажать кнопку «Построить гистограмму» для построения графика и вывода на экран.

Программа создает L диаметров D, высчитывает соответствующие им значения F. Значения F нормируются, т.е. каждое значение делится на последний элемент массива. Далее с помощью генератора случайных чисел генерируется число от 0 до 1 и сравнивается со значениями F. Берутся значения двух ближайших точек к данному случайному числу, и с помощью метода линейной интерполяции высчитывается диаметр частицы.

После этого строится график плотности распределения. Для вывода графика распределений используется модуль ZedGraph - компонент для рисования графиков под .NET Framework. Преимуществом данного модуля является возможность изменения масштаба графика одной кнопкой. Так же, в ZedGraph можно строить различные графики на одной панели (в данном случае нам необходимы гистограмма и кривая)[2]. Гистограмма показывает плотность созданных частиц, согласно указанному закону, а кривая – теоретически определенная плотность распределения.

Для построения гистограммы использовался следующий алгоритм:

1. Пользователь задает число М – число отрезков для построения гистограммы;

2. Рассчитывается шаг a,a1 для построения диаграммы;

3. Диаметр частицы, полученный методом Монте-Карло делится на шаг a,a1;

4. От полученного значения берется целая часть встроенным методом Math.Truncate(x). Составляем массив, смотрим, в какую ячейку попала частица, и увеличиваем счетчик на единицу в этой ячейке;

5. Шаги 4-5 повторяются N раз;

6. По полученным данным строится гистограмма.

3. Вторая вкладка

Вторая вкладка «Распределение частиц» см. Рисунок 3.

В качестве начальных условий здесь указываются:

После ввода всех условий, необходимо нажать кнопку «Создать частицы», тогда программа создаст случайным образом частицы, которые будут отражены в элементе panel.

Частицы на панели отрисовываются с помощью встроенного метода DrawEllipse, принадлежащего библиотеке System.Drawing.Graphics. Диаметр частиц и их положение определяются с помощью генератора случайных чисел.

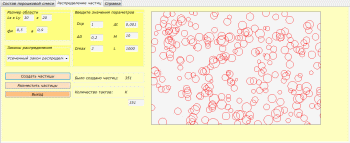
Рисунок 5. Создание частиц

При нажатии на кнопку «Разместить» с помощью метода вязкой суспензии частицы распределяются и занимают все доступное пространство.

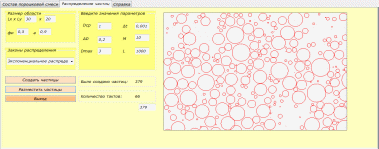
Рисунок 6. Размещение частиц

В качестве результатов исследования выводятся количество созданных частиц и число тактов, за которое частицы были распределены в пространстве.

ИССЛЕДОВАНИЕ

Целью исследования является, анализ скорости заполнения пространства частицами при различных значениях плотности «φ» и коэффициента «а» для усечено нормального распределения.

Для этого были проведены исследования в диапазоне параметров;

• ,

• .

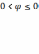При больших значениях φ и малых значениях а количество тактов очень большое. Для плотности φ = 0,8 число тактов очень велико даже при а близком к 1.

Я получила такие данные:

Таблица 1. Анализ скорости заполнения пространства частицами

a/фи	0,5	0,6	0,7	0,8
0,1	73	108	380	650
0,2	70	100	300	600
0,3	46	73	280	560
0,4	39	61	245	497
0,5	31	59	200	398
0,6	29	48	195	330
0,7	21	39	187	299
0,8	19	30	173	255
0,9	12	26	161	227
1	9	21	149	194

Исходя из этих данных, были построены следующие зависимости:

При = 0,5

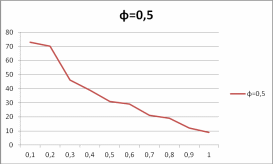
Рисунок 7. Зависимость скорость от «фи = 0,5»

При = 0,6

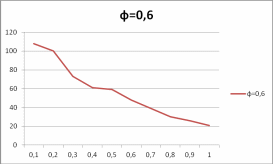
Рисунок 8. Зависимость скорости от «ф=0,6»

При =0,7

Рисунок 9. Зависимость скорости от «фи=0,7»

ВЫВОДЫ

В ходе курсовой работы был исследован метод вязкой суспензии для моделирования структуры дисперсных систем. Также был изучен метод Монте-Карло для моделирования частиц, используя различные распределения:

• Усеченной нормальное распределение;

• Гамма распределение;

• Экспоненциальное распределение;

• Логнормальное распределение.

Была создана компьютерная программа, реализующая следующие функции:

• Моделирование частиц в соответствии с заданными распределениями методом Монте-Карло.

• Моделирование размещения частиц в области с заданными размерами с помощью метода вязкой суспензии в соответствии с заданными распределениями методом Монте-Карло.

В ходе разработки программы были изучены и освоены некоторые функции языка C# и среды разработки Microsoft Visual Studio 2013:

• Компонент ZedGraph для построения графиков функций;

Было проведено исследование скорости размещения частиц в пространстве, в зависимости от плотности распределения, и значений параметров. Полученные результаты показали, что с возрастанием плотности «φ» и уменьшением параметра скорости «a» скорость размещения частиц в пространстве уменьшается. Для уменьшения времени расчетов при заданной плотности, параметр a должен быть равен 1.

СПИСОК ЛИТЕРАТУРЫ

1. Рашковский С.А., Курс лекций по предмету «Математическое моделирование сложных молекулярных структур». 2014 г.

2. Википедия — свободная энциклопедия [ru.wikipedia.org/wiki].

3. Шпаргалка по ZedGraph [jenyay.net/Programming/ZedGraph].