13.3. Критерій Севіджа

Використання критерію Вальда інколи приводить до суперечливих висновків. Розглянемо таку матрицю втрат (грн.).

=		S1	S2
	a1	50	210	210
	a2	150	200	200

Користуючись критерієм Вальда, приходимо до вибору альтернативи а₂. Інтуїтивно проситься вибрати а₁, оскільки не виключено, що S = S₁. Тоді втрати складуть тільки 50 грн. При виборі альтернативи а₂ втрати завжди будуть не меншими 150 грн.

Розглянемо критерій Севіджа, який ґрунтується на принципі мінімакса наслідків прийнятого помилкового рішення і старається мінімізувати втрачену вигоду. Його зміст полягає у формуванні нової матриці втрат з допомогою такої формули:

(13.2)

Отримані значення показують величину ризику, тому критерій Севіджа називають критерієм мінімального ризику. У першому випадку є різницею найкращого значення в стовпці S_j і значенням . За змістом, виражає «співчуття» особі, що приймала рішення, у зв’язку з тим, що вона не вибрала найкращої дії відносно стану S_j .

У другому випадку відображає різницю та найгірше значення в стовпці S_j .

Незалежно від того, чи є прибутком або втратами, функція в обох випадках визначає втрати. Тому до слід використовувати тільки мінімаксний критерій.

Отже, формула для вибору оптимальної альтернативи з допомогою критерію мінімального ризику набуває вигляду:

.

Приклад 13.3. Користуючись критерієм Севіджа, знайти розв’язок прикладу 13.1.

Розв’язування.

Відповідно до умови прикладу 13.1 матриця відображає втрати. Отже, для цього випадку має місце формула:

.

Знайдемо числові значення:

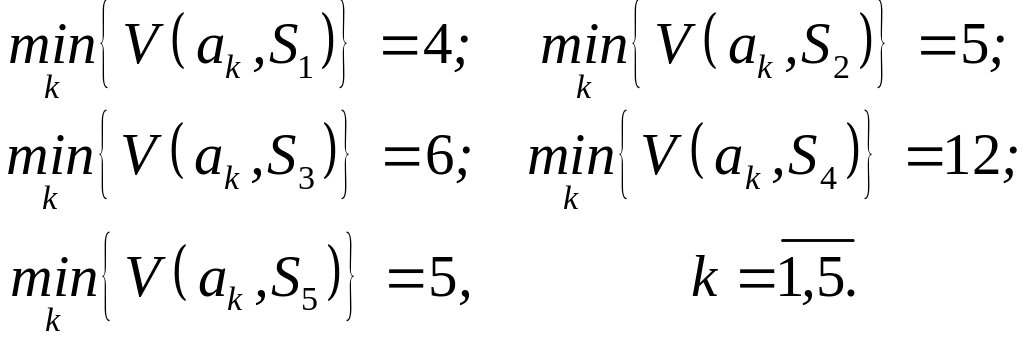
Тоді шукана величина ризику матиме вигляд (табл. 13.3).

Таблиця 13.3

=		S1	S2	S3	S4	S5
	a1	0	17	9	4	24	24
	a2	6	13	20	0	5	20
	a3	4	14	0	12	0	14
	a4	26	23	2	2	11	26
	a5	11	0	24	10	4	24

Отримуємо, .

Отже, найкращою альтернативою знову виявилася а₃. 

Розглянутий критерій досить часто використовується в практичній діяльності при прийнятті управлінських рішень на тривалий період. Наприклад, при розподілі капітальних вкладень на перспективу він дає добрі результати.

13.4. Критерій Гурвіца (критерій оптимізму-песимізму)

Критерій Гурвіца в своєму алгоритмі охоплює декілька підходів до прийняття рішень: від найбільш оптимістичного до найбільш песимістичного.

При найбільш оптимістичному підході можна вибрати альтернативу, яка дає , де є виграшем (прибутком).

Аналогічно для найбільш песимістичних припущень вибрана альтернатива відповідає

. (13.3)

Критерій Гурвіца встановлює баланс між випадками крайнього оптимізму й крайнього песимізму, порівнюючи обидві альтернативи з допомогою відповідних коефіцієнтів , та (–1), де 0  1. Якщо представляє прибуток, то вибираємо альтернативу, яка дає

. (13.4)

У випадку, коли представляє втрати, критерій вибирає альтернативу, яка дає

. (13.5)

Параметр  є показником оптимізму (ступенем впевненості): при =1, критерій дуже оптимістичний; при  = 0 – дуже песимістичний. Значення (0   1) може визначитися залежно від характеру особи, яка приймає рішення, тобто що їй більш характерно: песимізм чи оптимізм. Чим складніша господарська ситуація, чим більше в ній хоче підстрахуватись ОПР, тим ближче до нуля вибирається . Якщо  наближається до нуля, то збільшується невпевненість при досягненні успіху. Використання окресленого критерію ускладнюється при відсутності достатньої інформації про величину параметра , який в силу суб’єктивних причин при різних рішеннях і в різних ситуаціях набуває різних значень. При відсутності інформації про яскраво виражений характер особи  приймається рівним 0,5.

Припустимо, що  = 0, тобто ОПР має мало надії на сприятливий наслідок, тоді отримаємо:

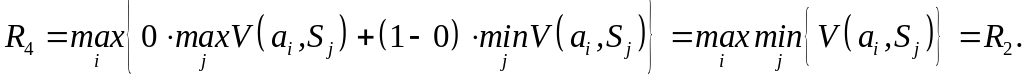При абсолютній впевненості в досягненні успіху (значення  приймаємо за 1) маємо крайній оптимізм:

.

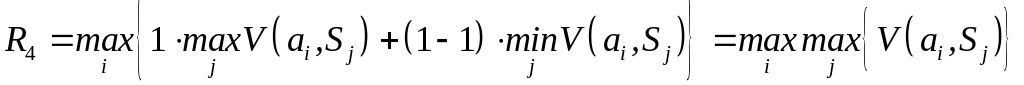За умови, що ОПР не має змоги визначити коефіцієнт , а компроміс між оптимістичним і песимістичним рішеннями бажаний використовуємо вираз:

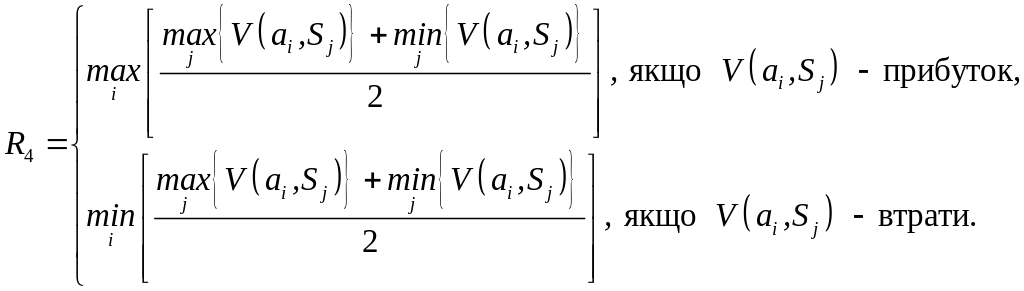(13.6)

Приклад 13.4. Користуючись критерієм Гурвіца, знайти розв’язок прикладу 13.1.

Розв’язування.

Використовуємо критерій Гурвіца до умови прикладу 13.1. Покладемо =0,5.

Для знаходження оптимального рішення побудуємо таблицю:

Таблиця 13.4

a1	4	29	16,5
a2	10	26	18
a3	5	24	14,5
a4	8	30	19
a5	5	30	37,5

.

Отже, оптимальне рішення полягає у виборі альтернативи а₃. 