4.4.5. Построение доверительных интервалов

Конечной целью моделирования является оценка или прогнозирование показателя Yв зависимости от значений X.

Прогноз подразделяется на точечный и интервальный и обычно осуществляется не более чем на одну треть размаха:

= 1108,34

где - точка прогноза.

В интервальном прогнозе отклонения от закономерностей в результате случайных воздействий определяются границами доверительных интервалов.

Доверительным интервалом называется такой интервал, которому с заданной степенью вероятности (называемой доверительной) принадлежат истинные значения показателя при условии, что закономерности, отраженные в модели, не противоречат развитию как на участке наблюдения, так и на участке оценки (или в периоде упреждения прогноза).

Случайные отклонения от модели проявляются в виде ошибок. Поэтому при определении границ, доверительных интервалов необходимо определить из чего складываются возможные ошибки моделирования, оценки и прогнозирования. При условии, что модель адекватна, и возможные ошибки носят случайный характер, следует различать два основных источника ошибок:

1. ошибки аппроксимации (рассеяние наблюдений относительно модели);

2. ошибки оценок параметров модели.

Ошибки оценок параметров модели обусловлены тем, что их параметры, фиксированные в модели как однозначные, в действительности являются случайными величинами, так как они оцениваются на основе фактических данных, в которых присутствует как закономерная, так и случайная составляющие. Средние значения этих оценок при выполнении предпосылок регрессионного анализа соответствует истинным значениям параметров, а их дисперсии зависят от остаточной дисперсии, числа наблюдений и вида модели.

Общеесреднее квадратическое отклонение истинных значений от расчетных может быть представлено как:

а в точке прогноза:

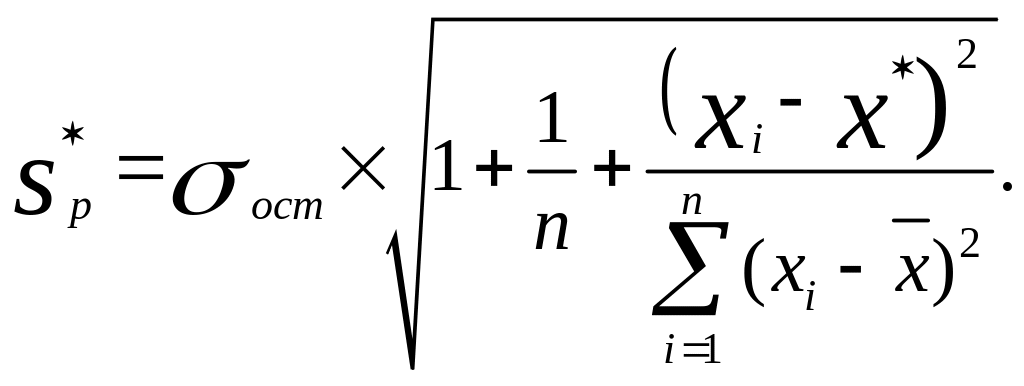
Исходя из предпосылки нормального распределения остатков границы доверительных интервалов определяются по формулам:

Анализ этих выражений позволяет для моделей парной регрессии сделать вывод, что доверительные интервалы тем шире, чем:

• больше остаточная дисперсия (менее точна модель);

• значение больше удалено от среднего значения ;

• сложнее форма модели;

• больше заданная доверительная вероятность.

ВЫВОД ИТОГОВ	Таблица 11
Регрессионная статистика
Множественный R	0,98
R-квадрат	0,96
Нормированный R-квадрат	0,96
Стандартная ошибка	0,87
Наблюдения	48

Таблица 12

Дисперсионный анализ
	df	SS	MS	F	Значимость F
Регрессия	1	1140,42	1140,42	1476,87	1,30
Остаток	46	35,52	0,77
Итого	47	1175,94

Таблица 13

		Коэффициенты	Стандартная ошибка	t-статистика	P-значение	Нижние 95%	Верхние 95%	Нижние 95,0%	Верхние 95,0%
Y- пересечение		-30,19	1,33	-22,61	1,48E-26	-32,882	-27,506	-32,88	-27,50
Переменная X1		0,06	0,00	38,43	1,31E-36	0,05	0,066	0,05	0,06

Таблица 14

ВЫВОД ОСТАТКА
Наблюдение	Предсказанное Y	Остатки	Стандартные остатки
1	12,97	-0,35	-0,41
2	13,15	-0,78	-0,90
3	13,22	-0,40	-0,46
4	13,66	1,80	2,07
5	15,51	-0,45	-0,90
6	15,83	-0,46	-0,93
7	16,36	-0,81	-1,64
8	16,58	-0,80	-1,62
9	16,69	-0,41	-0,83
10	16,73	-0,21	-0,42
11	17,18	-0,58	-1,17
12	17,28	0,12	0,24
13	17,29	0,15	0,30
14	17,45	0,02	0,04
15	17,47	0,02	0,03
16	17,53	0,02	0,04
17	17,96	0,10	0,19
18	18,68	-0,42	-0,85
19	19,03	-0,70	-1,42
20	19,03	-0,55	-1,11
21	19,09	-0,17	-0,35
22	19,12	0,06	0,13
23	19,38	-0,08	-0,16
24	20,67	-0,92	-1,07
25	21,24	-0,86	-0,98
26	21,35	1,77	2,04
27	19,79	-0,14	-0,29
28	21,83	0,84	0,96
29	19,99	-0,34	-0,69
30	20,06	0,51	1,04
31	20,39	-0,03	-0,06
32	20,48	0,46	0,94
33	20,56	0,76	1,53
34	20,81	0,60	1,21
35	21,44	-0,22	-0,45
36	21,74	-0,21	-0,43
37	21,76	0,13	0,27
38	21,88	0,20	0,41
39	22,27	-0,12	-0,24
40	22,30	0,29	0,58
41	22,31	0,69	1,39
42	22,61	0,42	0,85
43	22,90	1,04	2,11
44	23,89	-0,12	-0,24
45	27,7	0,21	0,24
46	29,9	1,49	1,71
47	32,0	0,34	0,39
48	32,9	0,22	0,25

В табл. 11 сгенерированы результаты по регрессионной статистике. Эти результаты соответствуют следующим статистическим показателям:

• множественныйR – линейному коэффициенту корреляции (ячейка D86):

• R-квадрат – коэффициенту детерминации ;

• НормированныйR-квадрат - скорректированное значение , вычисляемое по формуле:

• 

• стандартная ошибка– остаточному среднему квадратическому отклонению (78):

• наблюдения – числу наблюдений.

В табл. 12 сгенерированы результаты дисперсионного анализа, которые используются для проверки значимости коэффициента детерминации .

1. Столбец - число степеней свободы.

Для строки Регрессия число степеней свободы определяется количеством факторных признаков в уравнении регрессии .

Для строки Остаток число степеней свободы определяется числом наблюдений n и количеством переменных в уравнении регрессии .

2. СтолбецSS - сумма квадратов отклонений.

Для строки Регрессия – это сумма квадратов отклонений теоретических значений зависимой переменной от ее среднего значения

Для строки Остаток – это сумма квадратов отклонений эмпирических данных от теоретических

Для строки Итого– это сумма квадратов отклонений эмпирических данных от среднего:

или .

3. СтолбецMS – дисперсии, рассчитываемые по формуле .

Для строки Регрессия – это факторная дисперсия .

Для строки Остаток – это остаточная дисперсия .

4. Столбец F – расчетное значение F-критерия Фишера , вычисляемое по формуле

Столбец ЗначимостьF-значение уровня значимости, соответствующее вычисленному значению .

Столбцы табл. 13 имеют следующую интерпретацию:

1. Коэффициенты – значения параметров .

2. Стандартная ошибка – средние ошибки параметров .

3. t-статистика – расчетные значения t-критерия, вычисляемые по формуле

Р-значение – значения уровней значимости, соответствующие вычисленным значениям .

4. Нижние 95% и Верхние 95% - соответственно нижние и верхние границы доверительных интервалов для параметров регрессии .

Рассчитанные в табл. 13 коэффициенты регрессии позволяют построить уравнение, выражающее зависимость прибыли банков от суммы их активов:

Значение множественного коэффициента детерминации показывает, что 96,9% общей вариации результативного признака у объясняется вариацией факторного признака x. Следовательно, выбранный фактор существенно влияет на прибыль банков. Рассчитанный уровень значимости подтверждает значимость .

Так как попадает в критический интервал , т.е. , то гипотеза отвергается, т.е. множественный коэффициент детерминации является значимым и, следовательно, построенное уравнение адекватно генеральным данным и также является значимым.

Ошибка аппроксимации составляет 3,36%, следовательно, модель является достаточно точной.

Относительные показатели асимметрии и эксцесса (1,27 и 0,24) меньше 1,5, что позволяет сделать вывод о том, что эмпирическое распределение остатков не противоречит нормальному.

В табл.14 приведены значения параметров и и их средние ошибки. Сравнивая попарно значения параметров и их ошибок можно констатировать, что величина ошибок меньше значений параметров. К тому же эти параметры являются значимыми, о чем можно судить по значениям показателя P – значение в табл. 14, которые меньше заданного уровня значимости .

Среднее значение ряда остатков достаточно близко к нулю, т.е. модель не содержит постоянной систематической ошибки и адекватна по критерию нулевого среднего.

Стандартные остатки вычисляются по формулам:

_{= 0,86}

График стандартных остатков, построенный по данным табл. 14, приведен на рис. 13.

_{Рисунок 13}

Как видно из рисунка стандартные остатки укладываются в симметричную относительно нулевой линии полосу и не имеют как отрицательной, так и положительной тенденций. Модуль стандартных остатков меньше 3. Следовательно, дисперсии ошибок наблюдений можно считать постоянными.

Обобщая полученные результаты, можно сделать вывод, что построенная модель обладает хорошим качеством, т.е. она достаточно точна и адекватна исследуемому процессу по всем перечисленным ранее критериям. Учитывая еще и нормальность ряда остатков можно осуществлять точечный и интервальный прогнозы. В связи с этим табл. 15 приведены данные для построения доверительных интервалов.

Таблица 15
685,05	14,43	15,93	17,43	0,55
687,93	14,53	16,03	17,53	0,55
689,02	14,57	16,07	17,57	0,55
695,9	14,83	16,32	17,81	0,55
711,11	15,38	16,87	18,35	0,54
711,43	15,4	16,88	18,37	0,54
716,81	15,59	17,08	18,56	0,54
720,11	15,71	17,19	18,68	0,54
720,49	15,73	17,21	18,69	0,54
735,16	16,27	17,74	19,21	0,54
743,39	16,57	18,04	19,51	0,53
755,44	17,01	18,47	19,94	0,53
758,12	17,1	18,57	20,04	0,53
764,69	17,34	18,81	20,27	0,53
764,8	17,35	18,81	20,28	0,53
773,5	17,66	19,13	20,59	0,53
779,72	17,89	19,35	20,81	0,53
783,75	18,03	19,5	20,96	0,53
784,33	18,06	19,52	20,98	0,53
786,88	18,15	19,61	21,07	0,53
787,34	18,17	19,63	21,09	0,53
792,48	18,35	19,81	21,27	0,53
794,16	18,41	19,87	21,33	0,53
807,2	18,88	20,34	21,8	0,53
816,08	19,21	20,66	22,12	0,53
817,85	19,27	20,73	22,19	0,53
823,05	19,46	20,92	22,38	0,53
825,54	19,55	21,01	22,47	0,53
828,98	19,67	21,13	22,59	0,53
831,64	19,77	21,23	22,69	0,53
837,72	19,99	21,45	22,91	0,53
838,25	20,01	21,47	22,93	0,53
844,63	20,23	21,7	23,16	0,53
845,37	20,26	21,72	23,19	0,53
852	20,5	21,96	23,43	0,53
853,83	20,57	22,03	23,49	0,53
859,19	20,76	22,22	23,69	0,53
863,96	20,93	22,4	23,86	0,53
875,11	21,33	22,8	24,27	0,53
876,17	21,37	22,84	24,31	0,53
878,24	21,44	22,91	24,38	0,53
898,85	22,18	23,66	25,14	0,54
914,79	22,75	24,23	25,72	0,55
917,13	22,83	24,32	25,81	0,55
918,86	22,89	24,38	25,87	0,55
954,75	24,17	25,68	27,19	0,56
988,45	25,36	26,9	28,44	0,58
1002,52	25,85	27,41	28,96	0,59
1020,83	26,5	28,07	29,64	0,61
1160,67	31,37	33,12	34,87	0,75

Массив дополнен двумя значениями: и , которые выделены жирным шрифтом. Значения вычислены с доверительной вероятностью 0,975 и соответствующим ей коэффициентом доверия Стьюдента 2,01. Выбор распределения Стьюдента обусловлен достаточно большим значением относительного показателя асимметрии остатков.

График доверительных интервалов приведен на рис. 14.

Рисунок 14

С учетом нормального распределения остатков прогнозируемая прибыль составит от 31,37 до 34,87 млн. руб., при этом условное среднее (наиболее вероятный объем прибыли) ожидается 33,12 млн. руб.

ЛИТЕРАТУРА

1. Андронов А.М., Копытов Е.А., Гринглаз Л.Я.Теория вероятностей и математическая статистика: Учебник для вузов. – СПб: Питер. 2004. – 461 с.: ил. – (серия «Учебник для вузов»).

2. Боровиков В.STATISTICA. Искусство анализа данных на компьютере: Для профессионалов. 2-е изд. (+ CD). – СПб.: Питер. 2003. – 688 с.: ил.

3. Вуколов Э.А.Основы статистического анализа. Практикум по статистическим методам и исследованию операций с использованием пакетов STATISTICAи ECXEL: Учебное пособие. – М.: Форум: ИНФРА – М, 2004. – 464 с. – Профессиональное образование.

4. Громыко Г.Л. Теория статистики: Практикум. – 3-е изд., доп. и перераб. – М.: ИНФРА – М, 2006. – 205 с. – (Высшее образование).

5. Елисеева И.И., Юзбашев М.М.Общая теория статистики: Учебник/ Под ред. И.И. Елисеевой. – 5-е изд., перераб. и доп. – М.: Финансы и статистика. 2004. – 656 с.: ил.

6. Ефимова М.Р., Петрова Е.В., Румянцев В.Н.Общая теория статистики: Учебник. – 2-е изд., испр. и доп. – М.: ИНФРА – М, 2005. – 416 с. – (Высшее образование).

7. Макарова Н.В., Трофимец В.Я.Статистика в Excel: Учебное пособие. – М.: Финансы и статистика, 2002. – 368 с.: ил.

8. Салманов О.Н. Математическая экономика с применением Mathcad и Ecxel. – СПб.: БХВ – Петербург, 2003. – 464 с.: ил.

9. Скучалина Л.М., Павлова С.А.Статистические методы анализа, моделирования и прогнозирования внешнеторговых потоков на основе данных таможенной статистики: Учеб.пособие. – Люберцы: РИО РТА, 2000. – 67 с.: ил.

Сигел, Эндрю. Практическая бизнес-статистка: Пер с англ. – М.: Издательский дом «Вильямс», 2004. – 1056 с.: ил. – Парал. Тит.англ

49