2.4. Показатели дифференциации

1. Коэффициент фондовой дифференциации

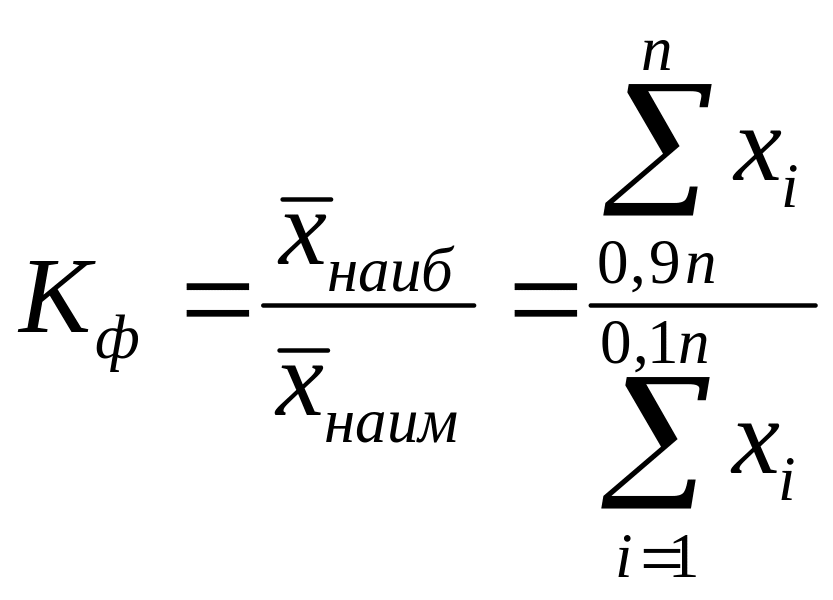
= 1,75 (24)

где - средние значения для 10% банков с наибольшими и для 10% с наименьшими значениями активов.

2. Коэффициент децильной дифференциации

= 1,34, (25)

где - максимальное значение активов у 10% банков с наименьшими активами;

- минимальное значение активов у 10% банков с наибольшими активами;

_{= 756,85}

- нижние границы интервалов, в которых находятся первая и девятая децили;

- ширины интервалов первой и девятой децили;

- сумма накопленных частостей в интервалах, предшествующих интервалам, в которых находятся первая и девятая децили;

- частости интервалов, в которых находятся первая и девятая децили.

2.5.Показатели концентрации

1. Кривая Лоренца

В статистике для изучения степени неравномерности распределения определенного суммарного показателя между единицами отдельных групп вариационного ряда используется кривая Лоренца (или кривая концентрации). Используя данные из таблицы 7, построим кривую Лоренца (Рисунок 6):

Рисунок 6

2. Коэффициент Джини

Рассчитывается на основе кривой Лоренца

, (26)

где ,

G= 0,16

Учитывая, что коэффициент Джинни равен 0,16, коннцентрация активов банков практически отсутствует.

2.6. Показатели формы распределения

Показатель асимметрии для сгруппированных данных находится из выражения:

= 0, 478 (27)

показатель эксцесса:

(28)

2.7. Проверка соответствия эмпирического распределения активов банков нормальному распределению с помощью критериев согласия Пирсона, Романовского и Колмогорова

1. Критерий Пирсона

(33)

где - эмпирические и теоретические частоты.

Другой подход к решению задачи основан на проверке попадания - критерия в критическую область, т.е. проверяется выполнение условия

.

_{= 5,99}

_2,89≤5,99

Условие выполняется, поэтому отклонения теоретических частот от эмпирических являются случайными и распределение активов банков не противоречит нормальному. Диаграмма эмпирических и теоретических частот приведена ниже (Рисунок 7).

Рисунок 7

1. Критерий Романовского

К_{р =} 0,26 < 3

Расчетное значение критерия равно 0,17, следовательно, расхождения теоретических и эмпирических частот являются случайными и несущественными.

1. Критерий Колмогорова ( )

О снован на определении максимального (по модулю) расхождения между накопленными частостями эмпирического и теоретического распределений (d):

_{= 0,54}

П о известному значению определяется вероятность , если она близка к 1, то расхождение между случайны.

=1

ВЫВОДЫ

1. В качестве характеристики центра распределения необходимо использовать среднюю арифметическую, т.к. совокупность является однородной (коэффициент вариации равен 9,54 %, что менее 33%).

2. Степень дифференциации активов банков слабая.

3. Концентрация активов банков практически отсутствует.

4. Распределение активов банков плосковершинно и имеет правостороннюю асимметрию. Отклонения эмпирических частот от теоретических носят случайный характер, следовательно, эмпирическое распределение активов банков не противоречит нормальному.