Тема I.3Сравнение нечетких множеств и операции над нечёткими множествами

1. Формула задает функцию принадлежности:

• Максминного пересечения нечётких множеств А и В

• Максминного объединения нечётких множеств А и В

• Максминной разности нечётких множеств А и В

• Максминной симметрической разности нечётких множеств А и В

2. Формула задает функцию принадлежности:

• Максминного объединения нечётких множеств А и В

• Граничной разности нечётких множеств А и В

• Максминного пересечения нечётких множеств А и В

• Максминной симметрической разности нечётких множеств А и В

3. Формула задает функцию принадлежности:

• Максминного объединения нечётких множеств А и В

• Алгебраического объединения нечётких множеств А и В

• Максминной разности нечётких множеств А и В

  • Максминной симметрической разности нечётких множеств А и В

4. Формула задает функцию принадлежности:

• Алгебраического объединения нечётких множеств А и В

• Алгебраической разности нечётких множеств А и В

• Максминной симметрической разности нечётких множеств А и В

• Максминной разности нечётких множеств А и В

5. Нечёткое множество А содержится в нечётком множестве В, если для всех элементов х из универсума Х функции принадлежности этих множеств связаны соотношениями:

• 

• µ_A(x) ≥µ_B(x)

• µ_A(x) =µ_B(x)

• µ_A(x) ˃µ_B(x)

6. Функции принадлежности нечётких множеств А и В для всех элементов х из универсума Х связаны соотношением . Это означает, что:

• Множество А содержится во множестве В

• Множество В содержится в множестве А

• Множество А равно множеству В

• Множество А равно пустому множеству

7. Функции принадлежности нечётких множеств А и В для всех элементов х из универсума Х связаны соотношением . Это означает, что:

• Множество В содержится в множестве А

• Множество А равно множеству В

• Множество А содержится во множестве В

• Множество В равно пустому множеству

8. Нечёткие множества А и В равны, если для всех элементов х из универсума Х функции принадлежности этих множеств связаны соотношениями:

• µ_A(x) ≥µ_B(x)

• µ_A(x) =µ_B(x)

• µ_A(x) ˃µ_B(x)

9. Формула µ_A(x) + µ_B(x) - µ_A(x)• µ_B(x) задает функцию принадлежности:

• Алгебраического объединения нечётких множеств А и В

• Алгебраической разности нечётких множеств А и В

• Алгебраической симметрической разности нечётких множеств А и В

• Максминной симметрической разности нечётких множеств А и В

10. Формула µ_A(x)•µ_B(x) задает функцию принадлежности:

• Граничного объединения нечётких множеств А и В

• Алгебраической симметрической разности нечётких множеств А и В

• Алгебраического пересечения нечётких множеств А и В

• Граничной симметрической разности нечётких множеств А и В

Тема I.4Расстояния между нечёткими множествами. Индексы нечеткости

1. Формула ρ(A,В)= задает :

• Расстояние Хемминга между нечёткими множествами А и В

• Евклидово расстояние между нечёткими множествами А и В

• Относительное расстояние Хемминга между нечёткими множествами А и В

• Относительное евклидово расстояние между нечёткими множествами А и В

2. Формула (A, B) = ² задает :

• Расстояние Хемминга между нечёткими множествами А и В

• Евклидово расстояние между нечёткими множествами А и В

• Относительное расстояние Хемминга между нечёткими множествами А и В

• Относительное евклидово расстояние между нечёткими множествами А и В

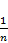
3. Формула (A, B) = задает :

• Расстояние Хемминга между нечёткими множествами А и В

• Евклидово расстояние между нечёткими множествами А и В

• Относительное расстояние Хемминга между нечёткими множествами А и В

  • Относительное евклидово расстояние между нечёткими множествами А и В

4. Формула(A, B)= ² задает :

• Расстояние Хемминга между нечёткими множествами А и В

• Евклидово расстояние между нечёткими множествами А и В

• Относительное расстояние Хемминга между нечёткими множествами А и В

• Относительное евклидово расстояние между нечёткими множествами А и В

5. Расстояние Хемминга между нечёткими множествами А и В задается формулой:

• (A, B)= ²

• (A, B)= ²

• (A, B) =

• ρ(A,В)=

6. Евклидово расстояние между нечёткими множествами А и В задается формулой:

• (A, B) = ²

• (A, B)= ²

• (A, B) =

• ρ(A,В)=

7. Относительное Евклидово расстояние между нечёткими множествами А и В задается формулой:

• (A, B) = ²

• (A, B)= ²

• (A, B) =

• ρ(A,В)=

8. Относительное Хеммингово расстояние между нечёткими множествами А и В задается формулой:

• (A, B) = ²

• (A, B)= ²

• (A, B) =

• ρ(A,В)=

9. Какие значения может принимать Хеммингово расстояние ρ(A,В)= между нечёткими множествами А и В:

•  ρ(A,В) Є [0;1]

•  ρ(A,В) Є [0;n]

•  ρ(A,В) Є (0;1]

•  ρ(A,В) Є [0;1)

10. Какие значения может принимать Евклидово расстояние между нечёткими множествами А и В (A, B) = ²:

•  ρ(A,В) Є [0;1)

•  ρ(A,В) < n²

•  ρ(A,В) Є [0;1]

•  ρ(A,В) Є [0; n^0,5]

11. Какие значения может принимать относительное Евклидово расстояние между нечёткими множествами А и В(A, B)= ²:

• ρ(A,В) Є (n; n²)

•  ρ(A,В) < n²

•  ρ(A,В) Є [0;1]

•  ρ(A,В) Є [0;n²]