2.2. Интервальные оценки и доверительные интервалы

Изучить:

а) понятия интервальной оценки и доверительного интервала;

б) построение интервальных оценок;

в) интервальные оценки числовых характеристик;

г) как влияет на величину интервала объем выборки и доверительная вероятность γ;

д) интервальная оценка вероятности события.

Оценки неизвестных параметров бывают двух видов – точечные и интервальные.

Точечная оценка – оценка имеющая конкретное числовое значение. Например, среднее арифметическое:

X = (x₁+x₂+…+x_n)/n, где: X – среднее арифметическое;

x₁,x₂,…x_n – выборочные значения;

n – объем выборки.

Интервальная оценка – оценка представляемая интервалом значений, внутри которого с задаваемой исследователем вероятностью находится истинное значение оцениваемого параметра.

Интервал в интервальной оценке называется доверительным интервалом, задаваемая исследователем вероятность называется доверительной вероятностью.

Задание 6

γ = 0,97 для варианта №20

6.1

Рассчитать доверительные интервалы для оценки математического ожидания признаков Х и Y. Уровень доверия γ выбрать в соответствии с номером задания на курсовую работу.

По распределению Стьюдента:

Для распределения X:

; ;

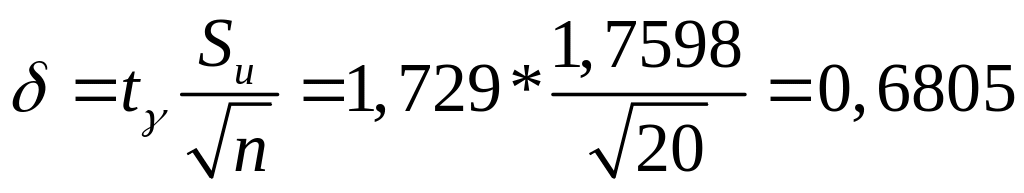
_{Доверительный интервал для мат. ожидания:}

Для распределения Y:

; ;

6.2

Рассчитать доверительные интервалы для оценки среднего квадратического отклонения признаков Х и Y. Уровень доверия γ выбрать в соответствии с номером задания на курсовую работу.

γ = 0,9 для варианта №23

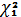1. Найдем и 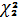по таблице Пирсона:

2. Доверительный интервал для СКО находиться по формуле:

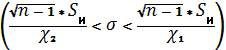
Для распределения X

; ;

Для распределения y:

3. Проверка статистических гипотез (тема 9)

3.1 Гипотезы о параметрах распределения

Изучить:

а) понятие статистической гипотезы. Классификация гипотез (параметрическая, непараметрическая, нулевая, альтернативная, простая, сложная);

б) понятия ошибок первого и второго рода;

в) статистический критерий проверки нулевой гипотезы;

г) уровень значимости статистического критерия и его связь с ошибками первого и второго рода. Критическая область и критические точки;

д) методика проверки статистических гипотез;

е) проверка гипотезы о генеральной средней при известной и неизвестной генеральной дисперсии;

ж) проверка гипотезы о генеральной дисперсии.

Статистическая гипотеза представляет собой некоторое предположение о законе распределения случайной величины или о параметрах этого закона, формулируемое на основе выборки. Гипотезы, в основе которых нет никаких допущений о конкретном виде закона распределения, называют непараметрическими, в противном случае – параметрическими.

Статистическая гипотеза называется непараметрической, если в ней сформированы предположения относительно вида функции распределения или закона распределения.

Статистическая гипотеза называется параметрической, если в ней сформулированы предположения относительно значений параметров функции распределения известного вида.

Нулевой гипотезой называют основную выдвинутую гипотезу и обозначают .

Альтернативной ( ) называют гипотезу, конкурирующую с основной в том смысле, что если нулевая гипотеза отвергается, то принимается альтернативная.

Статистическая гипотеза называется простой, если она имеет вид: .

Сложной называют гипотезу, которая состоит из конечного или бесконечного числа простых гипотез.

Статистический критерий проверки нулевой гипотезы:

1) Если выборка принадлежит критическому множеству , то отвергают основную гипотезу.

2) Если выборка не принадлежит критическому множеству , то нет оснований отвергать основную гипотезу.

Критическая точка – точка раздела между критической областью и областью допустимых значений. Критической областью называют совокупность значений критерия, при которых нулевую гипотезу отвергают.

1)Рассматриваются выборочные данные, и руководствуясь конкретными условиями задачи формулируем и .

Задаём уровень значимости критерия.

2)

3) выбираем критерий К по значениям которого мы можем судить о справедливости .

4) рассчитываем выборочную величину

5) определяем критические точки и критические области.

6) принятия статистического решения.

Проверка гипотезы основывается на вычислении некоторой случайной величины – критерия, точное или приближенное распределение которого известно.

Принятие или отклонение гипотезы Н₀ по случайной выборке соответствует истине с некоторой вероятностью и, соответственно, возможны два рода ошибок. Ошибка первого рода возникает тогда, когда отвергается верная гипотеза Н₀ и принимается конкурирующая гипотеза Н₁. Ошибка второго рода возникает в том случае, когда принимается неверная гипотеза Н₀, в то время как справедлива конкурирующая гипотеза Н₁. Доверительная вероятность – это вероятность не совершить ошибку первого рода и принять верную гипотезу Н₀. Вероятность отвергнуть ложную гипотезу Н₀ называется мощностью критерия.

Теорема Неймона - Пирсона: среди всех критериев заданного уровня значимости , проверяющих простую гипотезу против альтернативной гипотезы , критерий отношения правдоподобия является наиболее мощным критерием.