Задание 3

3.1

Для выборки признака X построить полигон и эмпирическую функцию распределения для статистического ряда.

X	58	59	60	61	62	63	64
ni	1	2	3	5	3	3	3
ni(нк)	1	3	6	11	14	17	20
pi	0,05	0,1	0,15	0,25	0,15	0,15	0,15
pi(нк)	0,05	0,15	0,3	0,55	0,7	0,85	1

Рис.3.1.1 (Полигон распределения для статистического ряда X)

Рис.3.1.2 (Эмпирическая функция распределения для статистического ряда X)

3.2

Для выборки признака Y построить полигон, гистограмму и эмпирическую функцию распределения для интервального ряда.

Yср	79	80,1	81,2	82,3	83,4	84,5
Интервалы	[78,45-79,55)	[79,55-80,65)	[80,65-81,75)	[81,75-82,85)	[82,85-83,95)	[83,95-85,05)
ni	4	3	2	2	6	3
ni(нк)	4	7	9	11	17	20
Pi	0,2	0,15	0,1	0,1	0,3	0,15
Pi(нк)	0,2	0,35	0,45	0,55	0,85	1
ni/h	3,63	2,72	1,81	1,81	5,45	2,72

Табл.3.2.2

Рис.3.2.1 (Полигон распределения для интервального ряда Y)

Рис.3.2.2 (Гистограмма распределения для интервального ряда Y)

Рис.3.2.3 (Эмпирическая функция распределения (кумулята) для интервального ряда Y)

2.Теория статистического оценивание параметров распределения (тема 8)

2.1. Точечные оценки характеристик положения и мер изменчивости.

Изучить:

а) числовые характеристики, описывающие центр распределения (среднее арифметическое, выборочные мода и медиана);

б) нахождение средней арифметической наблюденных значений случайной величины;

в) нахождение моды выборочной совокупности;

г) нахождение медианы выборочной совокупности.

д) понятие и формулы для нахождения выборочных начальных моментов;

е) понятие и формулы для нахождения выборочных центральных моментов;

ж) понятия и формулы для нахождения выборочной дисперсии, исправленной дисперсии, эмпирических коэффициентов асимметрии и эксцесса.

Среднее арифметическое значение выборочной совокупности рассчитывается по формуле:

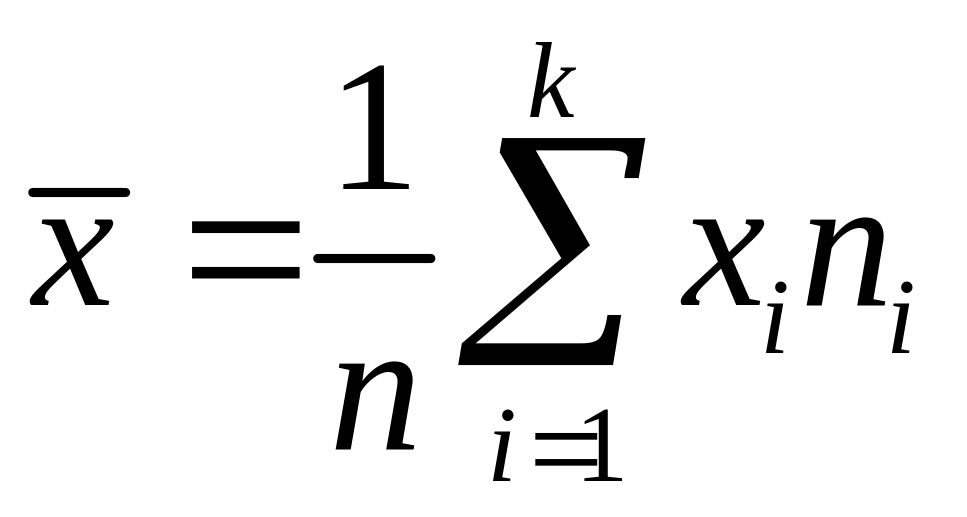
Мода ( ) - значение признака, которое наблюдалось наибольшее число раз.

Медиана ( ) - значение признака, приходящегося на середину ранжированного ряда наблюдений.

Если объем выборки равен 2k-1 (нечетное число), тогда медианой является то значение признака, которое приходится на середину ранжированного ряда наблюдений:

Если n=2k, тогда за медиану мы принимаем половину между и :

Для нашей задачи:

: _.

Аналогично статистическому ряду среднее арифметическое значение интервального ряда распределения рассчитываем по формуле:

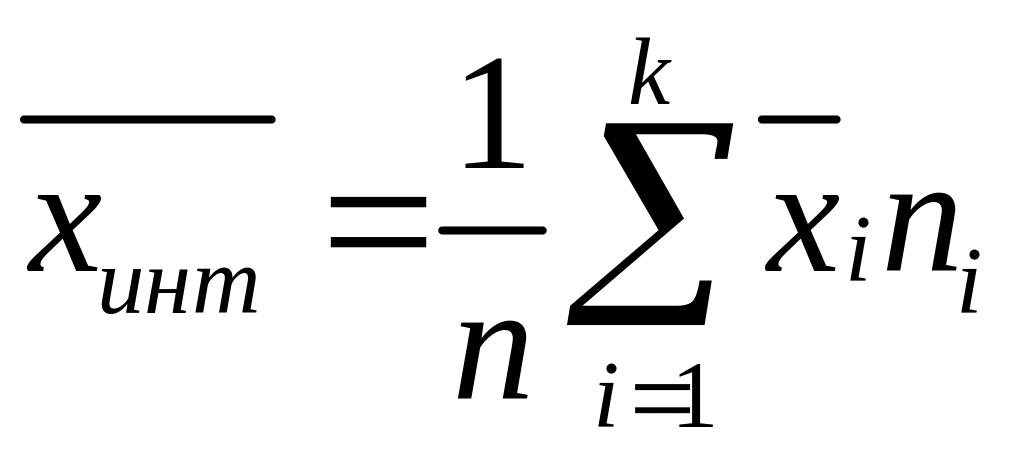
Мода для интервального ряда рассчитывается по формуле:

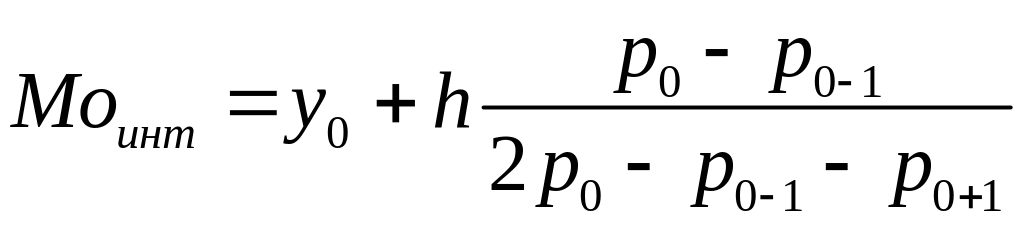
где - начало модального интервала;

- длина интервала (шаг);

- относительная частота модального интервала;

- относительная частота до модального интервала;

- относительная частота следующего за модальным интервала.

Медиана для интервального ряда рассчитывается по формуле:

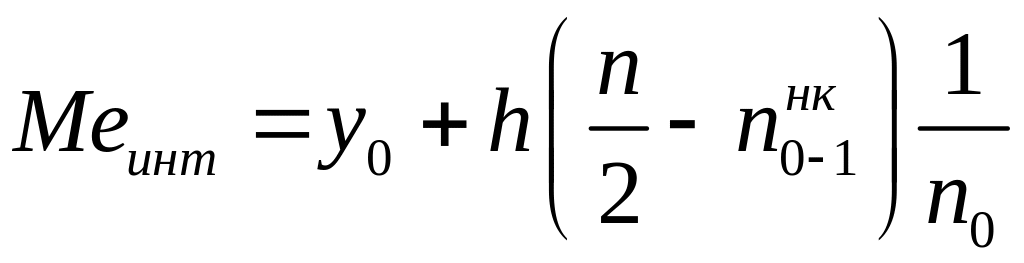
где - начало интервала;

- длина интервала (шаг);

- относительная частота интервала;

- относительная накопленная частота предыдущего интервала.

Если дана случайная величина X, определённая на некотором вероятностном пространстве, то -м начальным моментом случайной величины X, где   называется величина

и -м центральным моментом случайной величины   называется величина

Эмпирической (выборочной) дисперсией (S2) называют среднюю арифметическую квадратов отклонений результатов наблюдений от их средней арифметической:

В отличие от x̅ выборочная дисперсия имеет математическое ожидание, при любом n не равное дисперсии σ2 , но меньше этой величины на σ2/n. При больших n расхождение несущественно, при конечных же n мы можем «исправить» , помножив её на множитель n/(n-1).

Полученная таким образом исправленная выборочная дисперсия будет:

Выборочный коэффициент асимметрии равен

Выборочный коэффициент эксцесса равен