Задание 2
2.1
Для выборок признаков X и Y построить вариационный и статистический ряды распределения.
Вариационный и статистический ряд распределения X:
X |
58 |
59 |
60 |
61 |
62 |
63 |
64 |
ni |
1 |
2 |
3 |
5 |
3 |
3 |
3 |
ni(нк) |
1 |
3 |
6 |
11 |
14 |
17 |
20 |
pi |
0,05 |
0,1 |
0,15 |
0,25 |
0,15 |
0,15 |
0,15 |
pi(нк) |
0,05 |
0,15 |
0,3 |
0,55 |
0,7 |
0,85 |
1 |
Табл.2.1.1 (Статистический ряд распределения X)
,
Вариационный и статистический ряд распределения Y:
Y |
79 |
80 |
81 |
82 |
83 |
84 |
85 |
ni |
4 |
3 |
2 |
2 |
6 |
2 |
1 |
Табл.2.1.2(Статистический ряд распределения Y)
,
2.2
Для выборки признака X построить интервальный ряд распределения.
Интервальный ряд распределения X:
Составляем ряд распределения X используя статистический ряд распределения X по формулам:
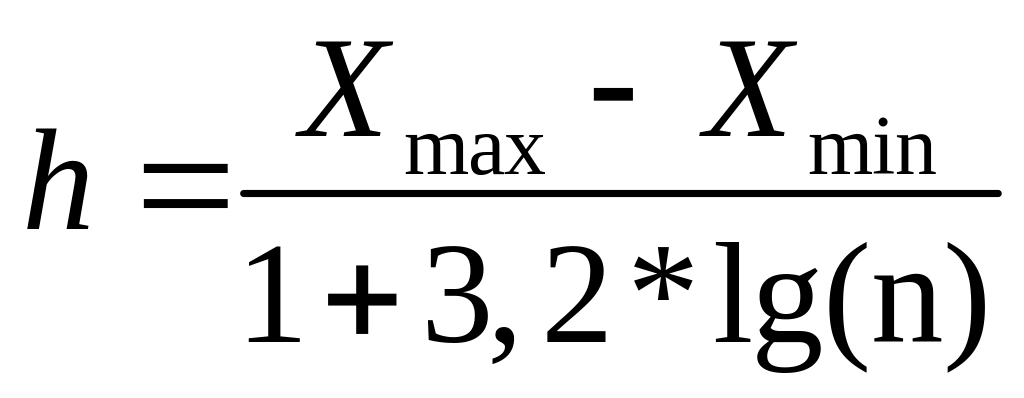
где
максимальное значение X,
-
минимальное значение X,
-
объем выборки.
Xср |
58 |
59,65 |
60,75 |
61,85 |
62,95 |
64,05 |
Интервалы |
[57,45-58,55) |
[58,55-59,65) |
[59,65-60,75) |
[60,75-61,85) |
[61,85-62,95) |
[62,95-64,05) |
Частота |
1 |
3 |
3 |
5 |
3 |
6 |
Табл.2.2.1(Интервальный ряд распределения X)
2.3
Для выборки признака Y построить интервальный ряд распределения.
Интервальный ряд распределения Y:
Составляем ряд распределения Y, используя статистический ряд распределения Y по формулам:
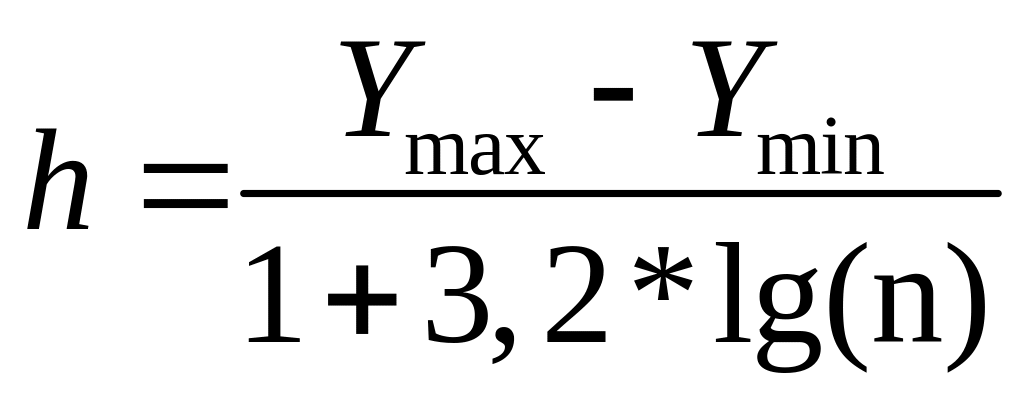
где
максимальное значение Y,
-
минимальное значение Y,
- объем выборки.
Yср |
79 |
80,1 |
81,2 |
82,3 |
83,4 |
84,5 |
Интервалы |
[78,45-79,55) |
[79,55-80,65) |
[80,65-81,75) |
[81,75-82,85) |
[82,85-83,95) |
[83,95-85,05) |
Частота |
4 |
3 |
2 |
2 |
6 |
3 |
Табл.2.3.1 (Интервальный ряд распределения Y)
1.3. Графическое представление рядов распределения
Изучить:
а) понятие полигона распределения и методику его построения;
б) понятие гистограммы и методику ее построения;
в) понятие эмпирической функции распределения и методику ее построения для дискретного и интервального рядов.
Полигон распределения. При построении полигона на горизонтальной оси (ось абсцисс) откладывают значения варьирующего признака, а на вертикальной оси (ось ординат) — частоты или частости.
Гистограммой частот (частостей) называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длины h , а высоты равны отношению ni/h – плотность частоты (pi*/h или ni/nh - плотность частости).
Для построения гистограммы по оси абсцисс указывают значения границ интервалов и на их основании строят прямоугольники, высота которых пропорциональна частотам (или частостям).
Эмпирической (выборочной) функцией распределения (или функцией распределения выборки) называется функция F*(x), задающая для каждого значения х относительную частоту события Х<х.
Кумулятивная кривая - это график выборочной функции F*(x), дающий приближенное представление о графике теоретической функции F(x)
(Кумулята – это сумма накопленных частностей)
Ряд распределения — представляет собой упорядоченное распределение единиц изучаемой совокупности на группы по определенному варьирующему признаку.