
- •Курсовая работа
- •Выполнил: курсант 37учебной группы
- •Санкт-Петербург
- •Содержание
- •Введение
- •Постановка задачи на выполнение курсовой работы (рабочая легенда)
- •1. Основные понятия выборочной теории (тема 7)
- •1.1 Выборочный метод
- •Задание 1
- •1.2. Построение статистических рядов распределения
- •Задание 2
- •1.3. Графическое представление рядов распределения
- •Задание 3
- •2.Теория статистического оценивание параметров распределения (тема 8)
- •2.1. Точечные оценки характеристик положения и мер изменчивости.
- •Задание 4
- •Задание 5
- •2.2. Интервальные оценки и доверительные интервалы
- •Задание 6
- •Для распределения y:
- •3. Проверка статистических гипотез (тема 9)
- •3.1 Гипотезы о параметрах распределения
- •Задание 7
- •3.2. Гипотеза о законе распределения
- •Задание 8
- •4. Корреляционный и регрессионный анализ (тема 10)
- •4.1. Корреляционная зависимость
- •Задание 9
- •4.2. Уравнение регрессии
- •Задание 10
- •Заключение
- •Список литературы
4.2. Уравнение регрессии
Изучить:
а) понятие парной линейной регрессии;
б) составление системы нормальных уравнений;
в) свойства оценок по методу наименьших квадратов;
г) методику нахождения уравнения линейной регрессии.
Предположим, что между двумя признаками Х и У существует некоторая взаимосвязь (корреляционная зависимость), при которой с изменением одного признака изменяется и другой, но каждому значению признака Х могут соответствовать разные, заранее непредсказуемые значения признака У, и наоборот.
Основная задача корреляционного анализа состоит в выявлении связи между случайными переменными путем точечной и интервальной оценок различных ( парных, множественных, частных) коэффициентов корреляции Дополнительная задача корреляционного анализа (являющаяся основной в регрессионном анализе) заключается в оценке уравнений регрессии одной переменной по другой.
Связь между признаками бывает положительной и отрицательной.
Если с увеличением (уменьшением) одного признака в основном увеличиваются (уменьшаются) значения другого, то такая корреляционная связь называется прямой или положительной.
Если с увеличением (уменьшением) одного признака в основном уменьшаются (увеличиваются) значения другого, то такая корреляционная связь называется обратной или отрицательной.
Задание 10
10.1.
Предположив, что между признаками X и Y существует линейная зависимость, найти коэффициенты уравнения регрессии Y на X и записать уравнение в виде y = b0 + b1x.
№ |
|
|
|
|
1 |
60 |
80 |
4800 |
3600 |
2 |
59 |
83 |
4897 |
3481 |
3 |
61 |
80 |
4880 |
3721 |
4 |
61 |
83 |
5063 |
3721 |
5 |
61 |
79 |
4819 |
3721 |
6 |
63 |
82 |
5166 |
3969 |
7 |
58 |
81 |
4698 |
3364 |
8 |
62 |
80 |
4960 |
3844 |
9 |
59 |
81 |
4779 |
3481 |
10 |
63 |
82 |
5166 |
3969 |
11 |
63 |
83 |
5229 |
3969 |
12 |
61 |
83 |
5063 |
3721 |
13 |
60 |
83 |
4980 |
3600 |
14 |
64 |
83 |
5312 |
4096 |
15 |
62 |
79 |
4898 |
3844 |
16 |
64 |
79 |
5056 |
4096 |
17 |
64 |
85 |
5440 |
4096 |
18 |
62 |
84 |
5208 |
3844 |
19 |
61 |
79 |
4800 |
3600 |
20 |
60 |
84 |
4897 |
3481 |
сумма |
1107 |
1470 |
90414 |
68137 |
Табл.10.1.1
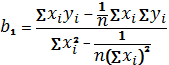
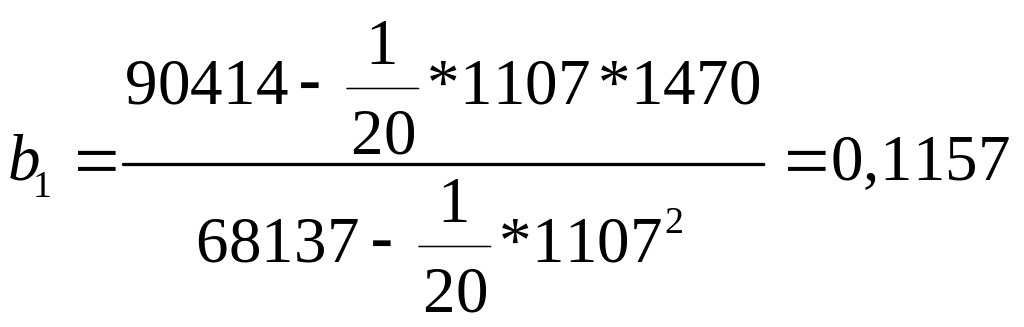
![]()
![]()
y = b0 + b1x.
![]()
10.2.
Построить полученную линию регрессии на поле корреляции признаков X и Y.

Рис.10.2 (линия регрессии)
