Задание 9

9.1.

По выборке X и Y построить поле корреляции и выдвинуть предположение о существовании (или не существовании) зависимости между признаками X и Y.

Рис.9.1

Из рисунка видно, что точки на графике расположены беспорядочно, соответственно можно сделать такой вывод, что корреляционной зависимости между признаками X и Y нет.

9.2.

Найти выборочный коэффициент корреляции и подтвердить (опровергнуть) вывод, сделанный в пункте 9.1.

Данные в корреляционной таблице представляют случайную выборку. Статистические числовые характеристики (S_х,S_y), полученные по этой выборке, являются оценками параметров генеральной совокупности, поэтому о тесноте зависимости между признаками X и Y мы судим по величине оценки коэффициента корреляции r. Следует проверить его значимость, т.е. установить – достаточна ли его величина при данном объеме выборки (n=20) для вывода о наличии корреляционной зависимости между признаками X и Y.

Выборочный коэффициент корреляции рассчитывается по формуле:

№
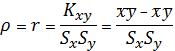
1	60	80	1,96	3,4596	2,604
2	59	83	5,76	1,2996	-2,736
3	61	80	0,16	3,4596	0,744
4	61	83	0,16	1,2996	-0,456
5	61	79	0,16	8,1796	1,144
6	63	82	2,56	0,0196	0,224
7	58	81	11,56	0,7396	2,924
8	62	80	0,36	3,4596	-1,116
9	59	81	5,76	0,7396	2,064
10	63	82	2,56	0,0196	0,224
11	63	83	2,56	1,2996	1,824
12	61	83	0,16	1,2996	-0,456
13	60	83	1,96	1,2996	-1,596
14	64	83	6,76	1,2996	2,964
15	62	79	0,36	8,1796	-1,716
16	64	79	6,76	8,1796	-7,436
17	64	85	6,76	9,8596	8,164
18	62	84	0,36	4,5796	1,284
19	61	79	0,16	8,1796	1,144
20	60	84	1,96	4,5796	-2,996
сумма	1107	1470	58,8	71,432	6,8

Табл.9.2.1

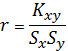
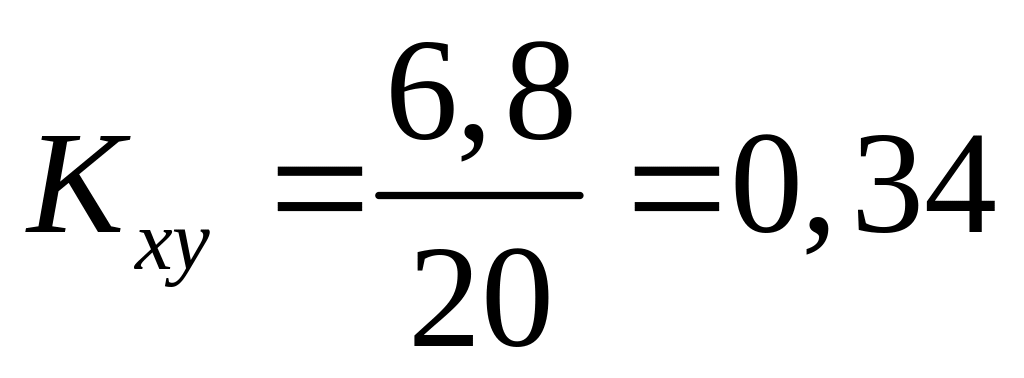
Так как значение коэффициента корреляции очень мало, то можно подтвердить предположение, сделанное в п. 9.1 и сказать, что связь слабая.

9.3.

Проверить гипотезу о значимости выборочного коэффициента корреляции.

Проверим значимость выборочного коэффициента корреляции r, т.е. установим достаточна ли его величина при данном объеме выборки для обоснованного вывода о наличии корреляционной связи.

1) H₀: r=0;

H₁: r 0

2) - уровень значимости.

3) По распределению Стьюдента:

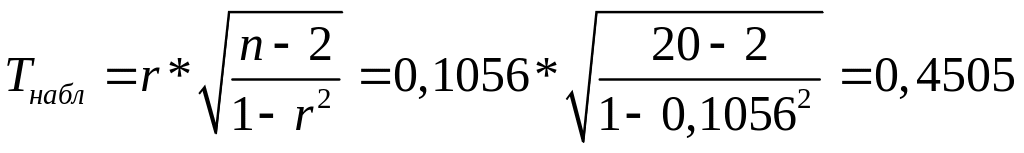
4) (двусторонняя критическая область)

Рис.9.3.1

Вывод: Гипотеза не отвергается , т.е. между признаками X и Y отсутствует корреляционная зависимость.