Интегралдың нолге тең болуы кейбір функцияның толық дифференциал екенін қөрсетеді. Яғни сол функция тек жүйенің күйімен ғана анықталадыда жүйе сол күйге келген жолға тәуелсіз болады.

, (13.2)

мұндағы күй функциясы энтропиядеп аталады.

Қайтымды процестер үшін энтропияның өзгерісі:

.

Қайтымсыз процестер үшін жүйенің энтропиясы өсіп отырады:

> . (13.3)

Бұл өрнектер тек тұйық жүйелер үшін орындалады. Жүйе сыртқы ортамен жылу алмасатын болса, онда оның энтропиясы кез келген жолмен өзгереді.

Клаузиус теңсіздігі: тұйық жүйенің энтропиясы немесе өседі (қайтымсыз процестер үшін), немесе тұрақты болып қалады (қайтымды процестер үшін).

.

Егер жүйе 1-ші күйден 2-ші күйге қайтымды процесс жасай ауысатын болса, онда энтропияның өзгерісі:

. (13.4)

Бұл формула көмегімен энтропияны аддитивті тұрақтыға дейінгі дәлдікпен анықтауға болады. Энтропияның өзінің физикалық мағынасы жоқ, физикалық мағына тек энтропияның айырмасында болады.

. (13.5)

Изотермиялық процесте:

. (13.6)

Изохорлық процесте:

(13.7)

Энтропия аддитивтік қасиетке ие болады: жүйенің энтропиясы, жүйеге кіретін денелер энтропияларының қосындысына тең.

Энтропия жүйе күйінің термодинамикалық ықтималдылығымен байланысқан.

Жүйе күйінің термодинамикалық ықтималдылығы деп берілген макрокүйді жүзеге асыратын микрокүйлердің санын атайды.

.

Больцман теңдеуіне сәйкес: (13.8)

Тасымалдау құбылыстарының жалпы теңдеуі

Тақырып: Тасымалдау құбылысы (2 сағ)

Негзігі сұрақтары:

1. молекулааралық өзара әсерлесу күші және потенциалы

2. орташа соқтығысу саны және орташа еркін жол ұзындығы

3. тасымалдау құбылысының физикалық мағынасы

4. тасымалдаудың жалпы теңдеуі

5. тасымалдау коэффициенттері және олардың арасындағы байланыстар

6. броундық қозғалыстың мағынасы

7. сиретілген газдардағы физикалық құбылыстар

Егер термодинамикалық жүйе тепе-теңдік күйде болмаса, жүйеде тасымалдау құбылыстары деп аталатын қайтымсыз ерекше процестер жүреді. Олардың нәтижесінде массаның, импульстің және энергияның кеңістіктегі тасымалдануы жүреді.

Тасымалдау құбылыстарына диффузия (массаның тасымалдануы), ішкі үйкеліс ( импульстің тасымалдануы) және жылу өткізгіштік ( энергияның тасымалдануы) жатады.

Тасымалдау құбылыстарының жалпы теңдеуі молекула-кинетикалық теория негізінде алынады.

Егер тасымалдау тек - осі бойымен өтетін болса, онда

, (10.17)

мұндағы - газдың тасымалданатын физикалық сипаттамасы,

- тасымалдану кезінде уақыт ішіндегі - осі бағытына перпендикуляр орналасқан аудан арқылы өтетін молекулалар саны, қатынасы - шамасының градиенті

10.10-сурет

Бұл жағдайдағы тасымалданатын шама – молекула массасы . Олай болса

,

ал

.

Сонда

.

, деп диффузия коэффициентін белгілесек,

, (10.18)

диффузия теңдеуін немесе Фик заңын аламыз.

Диффузия коэффициенті газ қысымына кері пропорционал (себебі ~ ) және температураның квадрат түбіріне тура пропорционал (себебі ~ )

Ішкі үйкеліс

Бұл жағдайдағы тасымалданатын шама – молекула импульсы . Мұндағы - газ қабатының жылдамдығы. Олай болса

,

ал

,

мұндағы - шекаралық аудандағы уақыт ішіндегі газ қабаттары импульстерінің өзгерісі. Сонда

.

, деп ішкі үйкеліс коэффициентін белгілесек,

(10.19)

ішкі үйкеліс теңдеуін немесе Ньютон заңын аламыз.

Ішкі үйкеліс коэффициенті қысымға тәуелсіз (себебі ~ , ал ~ ) және температураның квадрат түбіріне тура пропорционал. Бірақ вакуум үшін қысымға тәуелсіз, сондықтан ~ .

Бұл жағдайдағы тасымалданатын шама – молекуланың энергиясы

Олай болса ,

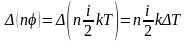ал ,

мұндағы - температураның кему бағытына перпендикуляр орналасқан

аудан арқылы уақыт ішінде тасымалданатын жылу мөлшері.

Сонда ,

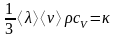деп жылу өткізгіштік коэффициентін белгілесек,

(10.20)

жылу өткізгіштік теңдеуін немесе Фурье заңын аламыз.

Жылу өткізгіштік коэффициенті қысымға тәуелсіз, себебі ~ , ал ~ . Бірақ вакуум үшін қысымға тәуелсіз, сондықтан ~ . Сиретілген газ үшін жылу өткізгіштік коэффициентінің қысымға тәуелділігі Дьюар ыдысында ( термос) пайдаланылады.

Тасымалдау коэффициенттерінің арасында мына байланыстар бар

, . (10.21)

Сұйықтар

Қатты дене мен газдың ортасынан орын алатын заттың агрегаттық күйі сұйық деп аталады. Сұйықтың кейбір қасиеттері қатты денеге, ал енді бір қасиеттері газға ұқсайды. Алайда сұйық газдан да, қатты денеден де өзгеше. Сұйық қатты дене сияқты белгілі бір формаға ие болмайды, ол ауырлық күшінің әсерінен өзі құйылған ыдыстың формасына ие болады. Газ молекулалары бір-бірімен молекулааралық күшпен байланыспаған болса, сұйық молекулалары бір-бірімен молекулааралық күшпен мықтап байланысқан.

Сұйық молекулалары бір-бірінен молекула мөлшеріндей (шамасындай) қашықтықта орналасады. Олай болса, сұйық молекулалары еркін қозғала алмайды. Сұйық молекулаларының қозғалысын алғаш Ян Френкель зерттеген. Оның пайымдауынша сұйық молекуласы біраз уақыт тепе-теңдік маңайында бір орында шамамен 10~¹⁰-10~¹² с тербеліп тұрады да, айналасындағы басқа бөлшектердің әсерінен өз орнынан ыршып кетіп, басқа орынға барып тербеледі. Сөйтіп, сұйық молекулалары бір орыннан екінші орынға көшіп жүреді.

Сұйықтар да газдар тәрізді, абсолют аққыш. Сүйыққа ауырлық күші әсер етпейтіндей жағдай жасасақ, ол шар формасына ие болады. Мұндай құбылыс салмақсыздық кезінде космос корабльдерінде байқалады.

Газдарға қарағанда сұйық өте нашар сығылады. Сұйықтардың бұл қасиеті олардың молекулаларынын, өте тығыз орналасуымен түсіндіріледі. Сұйықтың сығылу коэффициенті мынаған тең:

Мұндағы V- сұйықтың бастапқы көлемі, қысым Р-ға өскенде көлем 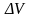-ға кішірейеді.

Сұйықтар жылулық ұлғаю коэффициентіне ие болады. Дененің, жылулық ұлғаю коэффициентін өлшейтін құралды дилатометр деп атайды. Қысым тұрақты болғанда сұйықтың көлемдік ұлғаю коэффициенті мына формуламен анықталады:

Сұйықтар, қатты денелер тәрізді беріктік қасиетке ие. Сұйық бағанының бірлік көлденең қимасына түсірілген күштің әсерінен сұйық бағанының үзілуін сұйық беріктігі деп атайды. Ол Н/м²-пен өлшенеді.

Бензолдың беріктігі 157* 10⁵ Н/м², ал судыкі - 280 * 10⁵ Н/м².

Молекулалық қысым. Беттік керілу

Температура аса жоғары болмаған кезде сұйықтардың молекулалық көлемі газдардың молекулалық көлеміне қарағанда әлдеқайда аз болады. Сұйық молекулаларының тартылу күші газ молекулаларының тартылу күшіне қарағанда көбірек, Сұйықтың ішінде (-сурет) (а) және бетінде (б) орналасқан екі молекуланы қарастырайық

«а» жағдайында орналасқан молекулаға оның жан жағында симметриялы түрде орналасқан молекулалар әсер етеді. Бұл молекулалардың қорытынды күші нөлге тең. Ал «б» жағдайында орналасқан молекулаға онын, төменгі, оң және сол жағында орналасқан молекулалар тарапынан күш әсер етеді де, ал үстіңгі жағынан күш әсер етпейді. Олай болса, «б» жағдайындағы молекулаға әсер ететін қорытынды күш нөлғе тең болмайды. Сұйық бетіндегі барлық молекулалар күші сұйыққа қысым түсіреді. Осы қысымды ішкі немесе молекулалық қысым деп атайды.

Бұл қысым Ван-дер-Ваальс теңдеуіндегі Р₁ ге тең. Молекулалық қысым - молекулалар арасындағы қысым, ол сұйыққа батырылған денеге берілмейді. Суреттен байқап отырғанымыздай f_к күштері (б) жағдайындағы молекулаға қарағанда бір-бірін теңестіреді. Ол күштердің қосындысы сұйықтардың беттік керілуі деп аталып, беттік керілу коэффициентімен сипатталады.

Қисық бетті сұйық астындағы қосымша қысым. Лаплас формуласы

Сұйықтың табиғатына, құрамына байланысты сұйық беті дөңес немесе ойыс болуы мүмкін. Осы ойыс немесе дөңес бетте беттік керілу күші нәтижесінде қосымша қысым пайда болады.

Дөңес бет астында пайда болған қосымша қысым төмен бағытталса, ойыс бет астындағы қысым жоғары қарай бағытталады (сурет). 1805 жылы Лаплас осы қосымша қысымды анықтайтын формуланы тұжырымдады.

,

мұндағы P – қосымша қысым, - беттік керілу коэффициенті,

R_1, R₂ - қисықтық радиустары.

Егер бет сфералық бет болса, онда R₁= R₂ =R болады да

Лаплас формуласы былайша өрнектеледі:

Дөңес бет үшін плюс таңбасы, ойыс бет үшін минус таңбасы қойылады.

Қосымша қысымды кейде Лаплас қысымы немесе капиллярлық қысым деп атайды.

Жұғатын және жұқпайтын сұйықтар. Жюрен формуласы

Егер қатты дененін, (мысалы, үстелдің) үстіне судын, бір тамшысын және сынаптың бір тамшысыи тамызсақ, онда олар әр түрлі формаға ие болатынын байқар едік. Су тамшысы үстел бетіне жайылып кетеді де, сынап тамшысы «жиырылып» шар формасына енеді.

Бірінші сұйықты (суды) жұғатын сұйық, екінші сұйықты (сынап) жұқпайтын сұйық деп атайды (сурет). Физикалық ұүрғыдан олар былайша түсіндіріледі.

Үш денеден: газ (ауа), сұйық (су, сынап), және қатты дене (үстелдің беті) тұратын жүйені қарастырамыз. Газ (ауа) бен сұйықтың (су, сынап) шекарасындағы беттік керілуін ₁₂, сұйық пен қатты дене (үстелдің беті) шекарасындағы беттік керілуді ₂₃, газ бен қатты дене шекарасындағы беттік керілуді ₁₃ деп белгілесек, онда жүйенің, шекаралары арасындағы тепе-тендік төмендегі жағдай орындалғанда ғана іске асады:

₁₃ = ₂₃ + ₁₂ cos ,

мүндағы — жиектік бұрыш деп аталады. Жиектік бұрыш — сұйыққа жүргізілген жанама мен қатты денеге жүргізілген жанамалардың арасындағы бұрыш.

Жұғатын сұйық үшін <90°, ал жұқпайтын сұйық үшіи >90° болады. Егер = 0° болса, онда сұйық қатты дене бетіне түгел жайылып кетеді (толық жұғу деп аталады). Ал = 180° болса, онда толық жұқпайтын кезең, басталады.

Біз қарастырған мысалда су үшін = 0°, ал сынап үшін = 180° болады. Айта кететін бір жайт сұйықтың жұғуы немесе жұқпауы, оның қандай қатты денемен әсерлесуіне де байланысты. Мысалы, су көптеген денелерге жұғатын болғанмен, майлы немесе шайырлы денелерге жұқпайды. Ал сынап көптеген қатты денелерге жұқпағанмен, мырышқа, қалайыға жұғады Диаметрі өте кішкене түтікшені капилляр деп атайды.

Осы капиллярды жұғатын сұйықтың ішіне салсақ, оның ішіндегі сұйықтың қисық беті ойыс болып келеді. Сұйық капиллярмен жоғары көтеріледі (а-сурет). Ал капиллярды жұқпайтын сұйыққа батырсақ, онда сұйық капиллярмен төмен түседі (б-сурет).Жұғатын сұйық капиллярмен қанша биіктікке көтеріледі, оны қалай табуға болады деген сұраққа жауапты Жюрен формуласы береді.

Радиусы r- ге тең капилляр жұғатын сұйыққа батырылған делік. Лаплас қысымының әсерінен сұйық капиллярмен h биіктікке көтерілсін. Капиллярдың ішіндегі сұйықтың салмағы (Р) Лаплас қысымының күшімен ( F ) теңелгенде сұйықтың көтеріліуі тоқталады, яғни :

Р = F,

бұдан . Мұндағы R – қисықтық радиусы.

Бұл формалаға енетін физикалық шамалардың тек R-ден басқалары белгілі.Атаптайтқанда, - сұйықтың беттік керілу коэффициенті, g - дененің еркін түсу үдеуі, - сұйық тығыздығы.

R -ді капиллярдың радиусы арқылы өрнектеу үшін АОК үшбұрышын қарастырамыз:

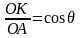немесе , осыдан . Осы мәнді формулаға қойсақ, шығатыны

, осы өрнек Жюрен формуласы деп аталады.Бұдан . Басқаша айтқанда капилляр жіңішке болған сайын, h –тың мәні көп болады.Капиллярлық құбылыс биологияда кеңінен пайдаланылады. Мысалы, ағаштың жоғарғы бөлігіне су мен басқа да ерітінділер осы капилллярлық құбылыс бойынша көтеріледі.

Бірінші және екінші текті фазалық ауысулар.Термодинамикада фаза деп өздерінің физикалық қасиеттері жөнінен системаның біртекті бірдей бөліктерінің жинағын айтады. Фаза ұғымын мынадай мысалдар арқылы түсіндірейік. Жабық ыдыста су және оның үстінде ауа мен су буының қоспасы тұр. Бұл жағдайда біз екі фазадан тұратын системамен істес боламыз: бір фазаны су, ал екіншіні - ауа мен су буының қоспасы құрайды. Егер суға бірнеше кесек мұз тастасақ, онда мұздың бұл кесектерінің бәрі үшінші фазаны құрайтын болады, себебі бұл мұз қатты фаза деп есептеледі. Әдетте, фаза деген ұғымды, заттардың агрегатты күйін сипаттайды деп атайды, бірақ оның мәні теріңірек. Қандай да бір заттың түрліше кристалдық модификациясы түрліше фаза болып табылады. Атап айтқанда, мысалы, алмас пен графит көміртегінің түрліше қатты фазаларына жатады.

Сонымен, заттың бір фазадан екінші түріне фазалық ауысуы, сол заттың қасиетінің сапалық өзгеруімен байланысты.

Фазалық ауысудың екі түрі бар. Бірінші текті фазалық ауысу (мысалы, балқу, кристалдану, т.б.) жылудың фазалық ауысуы деп аталатын белгілі – бір мөлшердегі жылудың жұтылуы мен немесе бөлінуімен жүреді. Бірінші текті фазалық ауысу температураның тұрақтылығымен және энтропия мен көлемнің өзгерістерімен сипатталады. Мысалы, тордың кристалдануы үшін, оның балқуы кезінде белгілі – бір мөлшерде жылу мөлшерін беру керек болады. Ал бұл жылу мөлшері денені қыздыру үшін емес атомаралық байланысты үзу үшін берілетіндіктен, балқу процесі тұрақты температурада жүреді. Олай болса, термодинамиканың екінші бастамасына сәйкес заттың реттелген кристалдық күйінің ретсіз сұйық күйіне осылайша ауысуының өсу дәрежесі жүйе энтропиясының артуымен байланысты. Егер ауысу кері бағытта өтетін болса, онда жүйе жылуды бөледі.

Екінші текті фазалық ауысу деп жылудың жұтылуына немесе бөлінуіне және көлемнің өзгеруіне байланыссыз болатын фазалық ауысуды айтамыз. Осы фазалық ауысу көлем және энтропияның тұрақтылығымен және жылу сыйымдылықтың секірмелі өзгерісімен сипатталады. Екінші текті фазалық ауысуды бірінші рет совет ғалымы Л.Д. Ландау (1908-1968) айтқан болатын.Екінші текті фазалық ауысуға белгілі бір қысым мен температурада ферромагнитті заттардың парамагнитті күйіне өтуі, металдармен кейбір қорытпалардың О К жақын температурада асқын өткізгіштік күйде болуы, электрлік кедергісінің секірмелі азаюының сипаттамасы, сұйық гелийдің (бірінші түрдегі гелий) Т = 2,9 К температурада өзінің басқа түріне өтуі (екінші түрдегі гелий), сөйтіп асқын аққыштық қасиетінің пайда болуы сияқты мысалдар жатады.

Белгілі бір жағдайларда бір заттың түрліше фазалары бірімен-бірі өз ара жанаса отырып, тепе-тендікте бола алады. Екі фазаның тепе-теңдігі температураның тек белгілі бір интервалында жүзеге аса алады, онда да температураның әрбір мәніне тепе-теңдік орнайтын р қысымның белгілі бір мәні сәйкес келеді. Сөйтіп, екі фазаның тепе-теңдік күйлері (р, Т) диаграммада мына сызықпен кескінделеді:

p =f (T). (1)

Атап айтқанда, мысалы, сұйық пен оның қаныққан буының тепе-теңдігі үштік нүкте температурасы мен кризистік температураның арасындағы температуралық интервалда байқалуы мүмкін. Бұл жағдайда қанықкан бу серпімділігінің қисығы (1) функцияның графигі болып табылады. Бір заттың үш фазасы (қатты, сұйық және газ тәрізді фаза, немесе екі қатты және бір сұйық фаза) температура мен қысымның бір жалғызақ мәнінде тепе-теңдікте тұра алады, бұларға (р,Т) диаграммасында үштік нүкте деп аталатын сәйкес келеді. Бұл нүкте жұбымен алынған фазалардың тепе-теңдік қисықтарының қиылысында жатады. .

Термодинамикада тәжірибелерге сәйкес тепе-теңдік күйде бір заттың көп болғанда үш-ақ фазасы болатындығы дәлелденді.

Бір фазадан екінші фазаға ауысу әдетте жасырын жылу, яғни жай жылу деп аталатын қайсыбір жылу мөлшерінің, жұтылуына немесе бөлініп шығуына байланысты болады. Кристалдық модификациялардың бір түрінен екінші түріне ауысуы кейде жылу мөлшерін жұтуға немесе бөліп шығаруға байланысты болмайды. Мұндай ауысулар, кәдімгі бірінші текті фазалық ауысулардан бөлек, екінші текті фазалық ауысулар деп аталады. Біз тек бірінші текті фазалық ауысуларды қарастыратын боламыз.

Булану және конденсация. Кез келген температурада сұйық және қатты денелерде энергиясы басқа молекулалардың сұйық немесе қатты дене бетінен бөлінуі үшін, тартылыс күштерін жеңіп шығуына, газ тәрізді күйге көшуіне жеткілікті, бірсыпыра молекулалар болады. Сұйықтың газ тәрізді күйге ауысуы булану деп аталады, ал қатты дененің газ күйіне ауысуы сублимация деп аталады.

Қатты денелердің бәрі, түгелінен, қай дәрежеде болғанымен сублимацияға (буға айналу) ұшырайды. Кейбір, мысалы, көмір қышқылы сияқты заттарда сублимация процесі елеулі жылдамдықпен өтеді; ал басқа заттарда бұл процестің, кәдімгі температуралардағы баяу өтуі соншалық, іс жүзінде ол сезілмейді.

Булану және сублимация кезінде денеден анағүрлым тез қозғалатын молекулалар шығып кетеді де соның салдарынан қалған молекулалардың орташа энергиясы азайып, дене суйды. Буланған (немесе сублимацияланған) дененің, температурасын тұрақты етіп ұстау үшін, оған сырттан үздіксіз жылу келтіріп тұру қажет. Булану температурасында тұрған заттың бір өлшем массасың түгелінен буға айналдыру үшін жұмсалатын жылу q меншікті булану (немесе сублимация) ж ы л у ы деп аталады.

Конденсация кезінде булануға жұмсалған жылу кері қайтарылады: конденсация кезінде пайда болған сұйық (немесе қатты дене) қызатын болады.

Сұйықтың булану жылуын есептеп шығарайық. Сұйық мөлшерінін, бір шама буланып, газ тәрізді фазаға ауысқан кезде, молекулалар беттік қабатта әсер ететін күштерге қарсы жұмыс өндірулері керек. Бұл күштер қабат қалыңдығына тең жолда әсер етеді. Бұл жолдағы күштердің орташа мәнін <f> арқылы, ал сұйқтың бірлік массасындағы молекулалар санын n арқылы белгілеп, беттік қабатта әсер етуші күштерге қарсы жұмысты п<f>r түрінде жазуымызға болады. Булану процесіне байланысты заттың көлемі өседі, осының салдарынан да сыртқы күштерге қарсы жұмыстың орындалу қажеттігі туады. Егер булану түрақты сыртқы р қысымда өтетін болса, сыртқы күштерге қарсы орындалатын жұмыс мынаған тең болады:

p(V_б - V_c ),

мұндағы V_б және У_с - бу мен сұйықтың меншікті көлемдері. Жоғарыда көрсетілген жұмыстардың екеуі де, q булану жылуының есебінен орындалады. Сөйтіп,

q= п<f>r - p(V_б - V_c ), (2)

Бұл (2) өрнектен, булану жылуы температураға байланысты азаятыны байқалады. Шынында да, температура артқан сайын қаныққан будың тығыздығы артады да, бұл өзінің, кезегінде беттік қабатта тұрған молекулаға әсер ететін күшті кемітеді. Сондай-ақ, қаныққан бу мен сұйықтың меншікті көлемдерінің айырмашылығы кемиді. Демек, температура артқан сайын (2) өрнектегі қосылғыштардың екеуі де азаяды. Кризистік температурада булану жылуы нольге айналады.

Сұйық пен оның буының арасында тепе-теңдік пайда болу процесін қарастырайық. Жарым-жартылай сұйық толтырған бітеу ыдысты алып ( 1-сурет), алғашқыда сұйық үстіндегі кеңістіктен зат түгел сорып алынған деп ұйғарайық. Булану салдарынан сұйық үстіндегі кеңістік молекулаларға тола бастайды. Газ тәрізді фазаға ауысқан молекулалар, хаосты қозғала отырып, сұйық бетімен соқтығысатын болады, содан бұл соқтығыстардың бір бөлегіне байланысты молекулалар сұйық фазаға ауысады. Уақыт бірлігінде сұйық фазаға ауысатын молекулалардың саны, сөз жоқ, сұйық бетіне соқтығысатын молекулалардың санына пропорционал болады, ал бұл өзінің, кезегінде поға пропорционал, яғни р қысымға байланысты өседі. Демек, буланумен қатар молекулалардың газ тәрізді фазадан сұйық фазаға көшуінің кері процесі жүріп жатаы және оның, интенсивтігі сұйықтың, үстіндегі кеңістікте молекулалар тығыздығы ұлғайған сайын өседі. Қысым (берілген температураға сәйкес) белгілі бір нақтылы мәнге жеткеннен кейін, сұйықтан шығып жатқан молекулалардың саны мен оған кері қайтып жатқан молекулалардың саны бірдей боп шығады. Осы мезеттен бастап, будың тығыздығының өзгеруі тоқталады. Сұйық пен будың арасында өзгермелі тепе-теңдік пайда болады (1-сурет) және ол системаның көлемі немесе температурасы қашан өзгергенге дейін бұзылмайды.

1 - сурет

Өзгермелі тепе-теңдікке сәйкес келетін қысым, қаныққан будың қысымы р_қ.б болып табылады. Егер ыдыс көлемін ұлғайтсақ, будың қысымы төмендеп кетеді де, тепе-теңдік бұзылатын болады. Соның нәтижесінде сұйықтың қосымша мөлшері буға айналады да, қысым тағы да р _к._б -ға тең. боп шығады. Осыған ұқсас көлемнің азаюы да будың бір шама мөлшерінің сұйыққа айналуына байланысты болады.

Уақыт бірлігінің ішінде сұйықтан бөлінІп шығатын молекулалар саны температураға байланысты күшті артады. Сұйық бетіне соқтығысатын молекулалар санының температураға байланыстылығы кемірек болад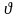ы (< > арқылы 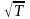ретінде). Сондықтан температураны арттырған кезде фазалар арасындағы тепе-теңдік бұзылады да, біршама уақыт ішінде сұйық - бу бағытындағы молеқулалар ағыны бу - сұйық бағытындағы молекулалар ағынынан басым болады. Бұл жағдай, қашан қысымның артуы, өзгермелі тепе-теңдікті қайта қалыптастырғанға дейін созылады. Сөйтіп, сұйық пен будың арасьнда өзгермелі тепе-теңдік пайда болатын қысым, яғни қаныққан будың қысымы, температураға байланысты болады.

Сұйық пен газдын. арасындағы тепе-теңдік жөнінде айтылғанның бәрін қатты дене-газ системасы үшін. де қолдануға болады. Әрбір температураға қатты дене мен газдың арасында өзгермелі тепе-теңдік қалыптасатын қысымның нақтылы мәні сәйкес келеді. Көптеген денелер үшін, мысалы, қатты металдар сияқты денелер үшін, бұл қысымның, кәдімгі температураларда аз болатыны сонша, оны өте сезгіш құралдар арқылы да анықтауға болмайды.

Балқу және кристалдану.Кристалдық дененің сұйық күйге көшуі әр зат үшін белгілі бір температурада өтеді де, балқу жылуы дейтін бір шама жылу мөлшерін жұмсауды қажет етеді. Алғашқыда кристалдық күйде түрған денеге минут сайын бірдей жылу мөлшері жұмсалса, онда дене температу р а с ының, уақытқа байланысты өзгеруі 2 -суретте көрсетілгендей болады. Бастапқы кезде дененің температурасы біртіндеп өседі. Балқу температурасына Т_бал жеткеннен кейін ( 2 -суреттегі 1 нүкте), денеге жылудың бұрынғыша берілгеніне қарамастан, онын температурасының өзгерісі тоқталады. Осы кезде қатты дененің балқу процесі басталады да, соның барысында заттың жаңа үлестері біртіндеп сұйыққа айнала береді. Балқу процесі аяқталғаннан кейін және зат толығымен сұйық күйге ауысып болғаннан кейін ( 2 -суреттегі 2 нүкте) температура тағы да жоғарылай бастайды.

Аморф дененің қыздыру қисықтығының түрі бұдан өзгеше (2 -суреттегі пунктирмен сызылған қисықты қараңыз). Бір қалыпты жылу берген жағдайда аморф дененің температурасы үздіксіз өседі. Аморф денелерде нақтылы сұйық күйге көшу температурасы болмайды. Бұл көшу секірмелі емес, үздіксіз жүзеге асады. Тек дененің жұмсауы қай температуралар шегінде жүзеге асатынын көрсетуге болады. Мұның өзі сұйықтар мен аморф денелер тек молекулаларының қозғалғыштық дәрежесімен айырылатынын - аморф денелердің, бұрын ескерткеніміз бойынша, күшті асыра суытқан сұйықтарға жататындығымен түсіндіріледі.

Балқу температурасы қысымға байланысты болады. Сөйтіп, кристалдық күйдің сұйық күйге ауысуы, қысым мен температураның мәндерімен сипатталатын белгілі бір жағдайларда жүзеге асады. Бұл мәндердің жинағына (р, Т) диаграммадағы балқу қисығы деп аталатын қисық сәйкес келеді. Балқу қисығы өте шұғыл болыпа келеді. Мұздың балқу температурасын, мысалы, 1 градусқақа өзгерту үшін, қысымды 132 ат-ға өзгерту керек.

Балқу қисығының нүктелері кристалдық фаза мен сұйық фазаның бір-бірімен тепе-теңдікте қандай жағдайларда тұра алатынын көрсетеді.

Балқуға кері кристалдану процесі мына түрде өтеді. Сұйықты берілген қысымда, қатты фаза мен сұйық фаза тепе-теңдікте бола алатын температураға дейін (яғни балқу басталатын температураға дейін) суытқан кезде, кристалдану ұрығы немесе кристалдану центрі дейтіндердің маңайында кристалликтердің жаппай өсуі басталады. Біртіндеп ірілене отырып, жеке кристалликтер ақыр аяғында өз ара бірігіп, поликристалдық қатты дене құрайтын болады.

Кристалдану центрлерінің ролін, сұйықтың ішінде қалқып жүрген қатты бөлшектер атқара алады. Осындай бөлшектерден әбден тазартылған сұйықты, кристалликтер пайда болмай-ақ, кристалдану температурасынан төменгі температураға дейін суытуға болады. Осындай асыра суытылған сұйықтың күйі метастабильді күйге жатады. Сұйықтың бірден тепе-теңдік температурадағы сұйыққа және кристалға жіктеліп кетуіне оған бір тозаңның түсіп кетуі жеткілікті. Алайда, кейбір жағдайларда сұйық молекулаларының қозғалғыштығы асыра суытқан кезде нашар болатындығы сонша, метастабильдік күй өте ұзақ уақыт сақтала алады. Мұндай жағдайларда сұйықтың аққыштығы өте нашар болады да, зат аморф қатты денеге айналады.

Кристалдану кезінде, балқу кезінде қанша жылу жұмсалса, сонша жылу бөлініп шығады.

Клапейрон — Клаузиус теңдеуі

Өткен параграфтардан біз заттың кез келген екі фазасының тепе-теңдік күйде шамасы температураға тәуелді болатын тек белгілі бір қысым кезінде ғана бола алатынын көрдік. Бұл тәуелділіктің жалпы түрін термодинамиканың екінші бастамасының көмегімен шығарып алуға болады. Ол үшін берілген заттың өз ара тепе-теңдіктегі екі фазасынан тұратың системаға қатысты Карно циклін қарастырайық.

Екі фазалық система үшін (р, V) диаграммасындағы Карно циклі 3-суретте көрсетілгендей болады (қыздырғыш пен суытқыш температураларының айырмасы өте аз шамасы деп ұйғарылып отыр). Температурасы Т изотерманың горизонталь учаскесінің шеткі нүктелері

1 және 2 цифрларымен белгіленген. 1 және 2 күйлер бір фазалы күйлер болып табылады. 1—2 кесіндісінің аралық нүктелерінің бәрі бір-бірінен зат массасының бірінші және екінші фаза арасында бөлінуі арқылы айырылатын екі фазалық күйлерді кескіндейді.

Изотермиялық процесс заттың қайсыбір m массасының фазалық ауысуымен байланысты болады. Сол кезде заттың көлемі - ға тең өсімше алады, мұндағы мен - бірінші және екінші фазалардың

м еншікті көлемдері. Мұндай ауысу жүзеге аса

алатын болу үшін, затқа mq₁₂ - ге тең Q₁ жылу мөлшерін беруге тиіспіз, мұндағы q₁₂ — Т температура жағдайында 1 күйден 2 күйге ауысқан кезде жұтылатын меншікті жылу. Q₁ жылу системаның циклдің барысында қыздырғыштан алатын жылуын білдіреді. Суытқышқа жылу изотермиялық процестің барысында беріледі. Берілген жылудың мөлшері мынаған тең: Q₂ = т'q₁₂ мұндағы - Т- температура жағдайында 1—2 ауысу жылуы, ал т'— процестің барысында фазалық ауысуға ұшыраған зат мөлшері. Заттың бұл мөлшерінің m - нен аз ғана айырмашылығы бар, өйткені заттың қайсыбір мөлшері адиабаталық процестің барысында фазалық ауысуға ұшырайды.

Цикл ішінде орындалатын жұмыс А сан жағынан, цикл ауданына тең. Сондықтан мынаны жаза аламыз:

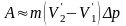( 1 )

Бұл (1) теңдеуі жуықтап алынған. нольге ұмтылған кездегі (ол үшін нольге ұмтылуы керек) шекте (1) өрнегі дәл теңдеуге айналады.

Цикльдің п. ә. коэффициенті анықтама бойынша мынаған тең:

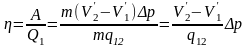(2 )

Сонымен қатар мынаны жазуға болады: (3)

(2) және (3) өрнектерді бірімен-бірін теңестіре отырып, үшін мынаны аламыз: . Бұдан , (4)

нольге ұмтылғандағы шекте (4) жуық теңдеу мынадай дәл теңдеуге айналады:

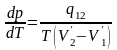(5)

Соңғы (5) қатысы Клапейрон - Клаузиус формуласы (немесе теңдеуі) деп аталады. Клапейрон - Клаузиус теңдеуі температура бойынша тепе-теңдік қысымнан алынған туындыны жылуға ауысумен, теңбе-теңдіктегі фазалардың температурасы және меншікті көлемдерінің айырымымен байланыстырады.(5) бойынша - туындының таңбасы, жылудың жұтылуы кезінде болатын фазалық өтумен қоса жүретін көлемнің езгерісіне - артуына немесе кемуіне тәуелді болады. Сұйық не қатты дене буланған кезде көлем әрқашан артады, сондықтан булану қисығы үшін, сондай-ақ сублимация қисығы үшін тек оң таңбалы болуы мүмкін: температураның артуы тепе-теңдік қысымның артуына әкеп соғады.

Балқыған кезде көлем әрқашан артады, демек, >0: қысымның ұлғаюы балқу температурасының Т артуына әкеп соғады. Алайда, кейбір заттарда, мәселен, суда сұйық фазаның көлемі қатты фазаның көлемінен

кем болады . Бұл жағдайда <0 — қысымның артуы балқу температурасының төмендеуімен қосарлана жүреді. Мұзды күшті қысымға ала отырып, оның балқу температурасын 0° С-тан арттырмай-ақ, ерітуге болады.

Бір кристалдық модификациядан екіншісіне ауысу температурасы, қысым артқанда қатты фазаның қайсысының меншікті көлемі артық болатынына қарай жоғарлауы да, төмендеуі де мүмкін. Су қатқан кезде көлемін ұлғайтатыны белгілі. Осы себепті де суға қарағанда мұздың тығыздығы аз болады.

Үштік нүкте. Күй диаграммасы. Затты сұйық күйінде алып онымен тепе-тендікте тұрған қаныққан буды қарастырайық та, көлемін өзгертпей одан біртіндеп жылу алатын болайық. Бұл процесс заттың температурасының төмендеуімен және соған сәйкес қысымының төмендеуімен байланысты болады. Сондықтан (р, Т) диаграммада зат күйінсуреттейтін нүкте төмен қарай булану қисығының бойымен қозғалатын болады (4 - сурет).Бұл қысымның тепе-теңдік мәніне жауап беретін заттың кристалдану температурасына жеткенге дейін созылады. Бұл температураны Т_үш арқылы белгілейік. Кристалдану жүріп жатқ ан уақыт бойы, температура мен қысым ұдайы тұрақты болып қала береді. Сол кезде сыртқа әкетіліп жатқан жылу, кристалдану кезінде бөлініп жатқан жылу боп табылады.

Температура Т_үш және соған сәйкес тепе-теңдік қысым р_үш - қатты, сұйық және газ тәрізді фаза сияқты заттың үш фазасының үшеуі де тепе-теңдікте тұратын температура мен қысымның жалғыз мәні. Диаграммадағы (р,Т) соған сәйкес нүкте үштік нүкте деп аталады. Сөйтіп, үштік нүкте заттың үш фазасының үшеуі де тепе-теңдікте тұра алатын шарттарды анықтайды. Кристалдану процесі аяқталғаннан кейін тепе-теңдік күйде қатты фаза мен газ тәрізді фаза қалады. Егер заттан жылу алуды одан әрі соза берсек, температура тағы төмендей бастайды. Соған сәйкес кристалдық фазамен тепе-теңдікте тұрған будың, қысымы да азая бастайды. Зат күйін көрсететін нүкте сублймация қисығының бойымен төмендей бастайды.

Ү штік нүкте температурасы, р_үш қысымда тұрып заттың балқитын температурасы болады. Бұдан басқа қысымдарда заттың, балқу температурасы басқаша болады. Заттың балқу қысымы мен балқу температурасының арасындағы байланыс үштік нүктеден басталатын балқу қисығы арқылы кескінделеді. Сөйтіп, үштік нүкте қатты және сұйық, сұйық және газ, ақырында, қатты және газ күйлерінін тепе-теңдік

(5 – сурет) жағдайларын анықтайтын үш қисықтың қиылысқан нүктесі болады.

Қатты және сұйық фазаның меншікті көлемдерінің қатысына байланысты, балқу қисығының барысы не 4 -суретте көрсетілгендей болады, не 5 -суретте көрсетілгендей болады.

Балқу, булану және сублимация қисықтары, координата жазықтығын үш облысқа бөледі. Сублимация және балқу қисықтарының сол жағында қатты фаза облысы, балқу және булану қисықтарының арасында сұйық күйлер облысы, ақыр аяғында, булану мен сублимация қисықтарының оң жағында заттың газ күйлерінің облысы жатыр. Бұл облыстардың бірінен қалауымызша алған нүкте заттың сәйкес бір фазалы күйін көрсетеді (біз ұдайы тек тепе-теңдік күйді, яғни заттың сыртқы жағдайлар тұрақты болғанда, қанша ұзақ болса да тұра алатын күйін сөз етіп отырмыз). Бұл облыстарды шектейтін қисықтардың біреуінде жатқан кез келген нүкте, заттың тиісті екі фазасының тепе-теңдік күйін көрсетеді. Үштік нүкте үш фазаның барлығының тепе-тендік күйін кескіндейді.

Сөйтіп, диаграммадағы әрбір нүкте заттың белгілі бір тепе-теңдік күйін кескіндейді. Сондықтан да оны к ү й диаграммасы деп атайды.

Дағдылы заттардың көпшілігінде үштік нүкте атмосфералық қысымнан едәуір төмен жатады, сондықтан бұл заттардың қатты күйден газ тәрізді. күйге өтуі екг арадағы сұйық фаза арқылы жүзеге асады. Атап айтқанда, мысалы, судың үштік нүктесіне 4,58 мм. сын. бағанасындағы қысым және 0,0075° С температура сәйкес келеді.

Көмір қышқылы үшін үштік нүкте қысымы 5,11 ат -ға тең (үштік нүкте температурасы - 56,6°С). Сондықтан көмір қышқылы атмосфера қысымында тек қатты және газ тәрізді күйлерде ғана болады. Қатты көмір қышқылы (құрғақ мұз) тікелей газға айналады. Көмір қышқылының атмосфералық қысымдағы сублимация температурасы - 78°С-қа тең.

Қорыта келіп, күй диаграммасының тағы бір ерекшелігін атап өтейік. Булану қисығы кризистік К нүктесімен аяқталады. Сондықтан сұйық күйлер облысынан газ тәрізді күйлер облысына кризистік нүктені айналып, булану қисығын қимай-ақ ауысуға мүмкіншілік туады (4-суретте пунктирмен көрсетілген 3-4 ауысуды қараңыз). Мұндай ауысудың (р, V) диаграммада қандай болып келетіні 276-суретте көрсетілген. Бұл жағдайда сұйық күйден газ тәрізді күйге ауысу (және керісінше) бір фазалық күйлердің тізбегі арқылы үздіксіз жүзеге асады.

Сұйық және газ күйлердің арасында үздіксіз ауысудың мүмкін болатыны оларды айырмашылық сапалық жағынан гөрі тек сандық сипатты айырмашылықтың болуында, атап айтқанда, бұл күйлердің екеуінде де анизотропия болмайды. Кристалдық күйден сұйық немесе газ тәрізді күйге үздіксіз ауысу мүмкін емес, өйткені кристалдық күйдің басты ерекшелігіне, өзімізге белгілі, оның анизотропиясы жатады. Ал, анизотропиясы бар күйден, анизотропиясы жоқ күйге өту тек секірмелі жүзеге асуы мүмкін анизотропияның жарым-жартылай пайда болуы мүмкін емес, анизотропия не бар, не жоқ болуы мүмкін, үшінші мүмкіншілікке жол жоқ. Осы себепті сублимация қисығы мен балқу қисығы, булану қисығының кризистік нүктеде үзілетіні сияқты, үзіліп қала алмайды. Сублимация қисығы р = 0 және Т = 0 нүктесіне барады да, ал балқу қисығы шексіздікке кетеді.

Тап солай, бір кристалдық модификациядан екіншіге үздіксіз ауысу мүмкін емес. Түрліше кристалдық модификациялар бір-бірінен өздеріне тән симметрия элементтері арқылы өзгеше боп келеді. Кез келген элемент симметриясы не бар, не жоқ болып келетіндіктен, бір қатты фазадан екіншіге ауысу тек секірмелі өтуі мүмкін. Сол себепті, екі қатты фазаның, теңбе-теңдік қисықтары булану қисығы сияқты, шексіздікке кетеді

Машықтану сабақтары

Тақырып: МКТ ның негізгі теңдеуін қолдану

1- есеп. Массасы =5 г. мыстан жасалған тиындағы атомдар саны мен олардың концентрациясын анықтаңдар. Мыс атомының мөлшерін бағалаңдар. Мыстың тығыздығы =8600 кг/м³.

Шешуі.

Мыс атомдары санын формуласы бойынша анықтаймыз. Мұндағы – мыстың мольдік масссы. Қатты денедегі атомдар бір-біріне жақын орналасқандықтан атом өшлемі шамамен атомдар арасына тең, сондықтан:

.

ның өлшемділігін анықтаймыз :

; ;

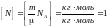Берелген шамалардың өлшемділігін БХЖ жазып, есептеу жүргіземіз :

, , .

, ; .

2 – есеп. Сутегінің бір бөлігінен ( массасы бойынша) және оттегінің сегіз бөлігінен тұратын газ қоспасының мольдік массасын газ анықтаңдар. водорода.

Шешуі.

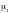Сутегі мен оттегінің массаларын и , мольдік массаларын - и

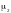
деп белгілейік. Қоспаның мольдік массасы

, мұндағы - қопадағы зат мөлшері

,

мольдік массаның формуласын ескеріп төмендегі өрнекті аламыз:

.

Есептің шарты бойынша болғандықтан , дің өрнегі төмендегідей болады:

Мольдік μ массаның өлшемділігін анықтаймыз μ :

.

Берелген шамалардың өлшемділігін БХЖ жазып, есептеу жүргіземіз:

,

№5.2, №5.4, №5.6, №5.8, .№5.10. (Волкенштейн В.С. Жалпы физика курсының есептер жинағы., Алматы, Мектеп, 1974) есептерді шығарыңыздар

Тақырып: Максвелл және Больцман таратылуы

1- есеп.

температурадағы оттегі молекулаларының ықтимал, орташа ,орташа квадраттық жылдамдықтарын анықта. Жылдамдықтары ықтимал жылдамдықтан айырмашылығы 1% тен аспайтын молекулалардың салыстырмалы санын , есептеңдер.

Шешуі.

Молекулалардың ықтимал, орташа ,орташа квадраттық жылдамдықтары ілгеріде анықталған формулалар бойынша есептеледі. Есептеу жүргіземіз:

, ,

.

Жылдамдықтары ықтимал жылдамдықтан айырмашылығы 1% тен аспайтын молекулалардың салыстырмалы санын , есептейміз: Жылдамдықтар мәндерінің интервалы

,

болғандықтан іздеп отырған молекулалар саны:

2 - есеп.

Самолет бортындағы барометр үнемі тұрақты р=79 кПа қысымды көрсетеді,сондықтан летчик биіктікті тұрақты деп есептейді. Алайда қолшаған ауаның температурасы с t₁ = 5 °С тан t₂=1 °С ге өзгерді. Какую Биіктікті анықтада ұшқыш қаншалықты 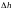қателік жіберді? Жер бетіндегі қысым 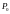қалыпты.

Шешуі.

Барометрлік формуланы h₁ және h₂ үшін жазамыз :

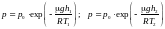(1)

қатынастарып тауып теңдіктерді логарифмдейміз:

(2)

шыққан теңдеулерден ді анықтап, айырмаларын табамыз:

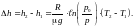(3)

(3) ге шамалардың мәндерін қойып = —28,5м. ді аламыз.

таңбасы болатынын көрсетеді , яғни самолдет , самолет 28,5 м ге төмендеген.

№5.94; №5.96; №5.98; №5.100; (Волкенштейн В.С. Жалпы физика курсының есептер жинағы., Алматы, Мектеп, 1974) есептерді шығарыңыздар.

Тақырып. Термодинамиканың бірінші бастамасы

1- есеп

Идеал газ адиабаталық сығылады.Осы жағдай үшін молекулалардың еркін жүру жолының орташа ұзындығының қысымға және уақыт бірлігіндегі соқтығысу санына тәуелділігін анықтаңдар.

Шешуі.Молекулалардың еркін жүру жолының орташа ұзындығының : формуласы және идеал газ күйінің теңдеуіне сәйкес : өрнегін аламыз.

Адиабата теңдеуінен: , мұндағы .

: .

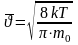Осыған сәйкес : , деп есептеп және , ескеріп 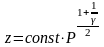өрнегін аламыз.

2- есеп.

Массасы m₁=1г оттегінен және массасы m₂=8г гелийден тұратын t = 27 температурадағы газ қоспасының U ішкі энергиясын анықта.

Шешуі.

Оттегі – екі атомды газ, t = 27 температурада айналмалы еркіндік дәрежелері қозбайды. Сондықтан оттегінің еркіндік дәреже саны i₁=5. Гелий – бір атоды газ, еркіндік дәреже саны i₂=3. Қоспаның ішкі энергиясы формулсымен есептейміз (4.1.37):

.

Ішкі энергияның өлшемділігін анықтаймыз :

Берелген шамалардың өлшемділігін БХЖ жазып, есептеу жүргіземіз :

.

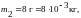
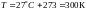3- есеп

Көлемі = оттегінің қысымы =200 кПа. Газ әуелі тұрақты қысымда = көлемге дейін қыздырылған, одан кейін тұрақты көлемде =500 кПа қысымға дейін қыздырылды. Процесстің графигін салыңыздар және :

1) газдың U ішкі энергиясының өзгерісін ;

2) А атқарған жұмысын; 3) Q газға берілген жылу мөлшерін анықтаңыздар

Шешуі.

Процестің графигін саламыз ( 1сурет). Графикте 1, 2, 3 нүктелерімен газдың пара­метрлері мен сипатталатын күйлері кескінделген

1- сурет

Газдың 1-күйінен 3-ге өткен кездегі U ішкі энергиясының өзгерісі

U= ∙ ΔT, формуласымен анықталады (1)

— көлем тұрақты кезіндегі мольдік жылу сыйымдылық ; m — газдың массасы; ΔT - және 3-күйлерге сәйкес температуралар айырмасы, яғни.

, болғандықтан (2)

Онда . (3)

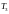және температураларды Менделеев— Кла­пейрон теңдеуінен өрнектейміз:

(4)

(4.4.2.4) өрнегін ескергенде (4.4.2.3) төмендегідей жазылады:

(5)

(5) ге шамалардың мәндерін қойып және оттегі екі атомдық газа, =5 ті ескеріп, есептеу жүргіземіз:

=3,25 МДж.

Газдың атқарған толық жұмысы А= , мұндағы — газдың 1—2 бөліктегі атқарған жұмысы; — ( 2—3) бөліктегі жұмыс.

1—2 аралықта қысым тұрақты (p=const). Бұл аралықтағы жұмыс формуласымен есептеледі. (2—3) аралықта газдың көлемі тұрақты болды, сондықтан ( =0). Сонымен

A= .(4.4.2.6)

(6) формулаға физическалық шамалардың мәндерін қойып есептеу жүргізіп:

а=0,4 МДж.

шамасын аламыз.

Термодинамиканың бірінші бастамасына сәйкес Q газға берілген жылу мөлшері:

Q= =3,65 МДж.

4- есеп .

Цилиндрде массасы =0,02 кг Т = З00 К. температурадағы сутегі газы бар. Газ адиабаталық ұлғайып көлемін 5 есе арттырды.Содан кейін изотермиялық сығылып көлемін 5 есе азайтты. Адиабаталық ұлғаю соңындағы Т₂ тем­ператураны және А газдың атқарған жұмысын есептіңідер.Процесті график арқылы кескіндеңіздер.

Шешуі.

Адиа­баталық процесс атқаратын газдың температуралары мен көлемдерінің арасындағы байланыс төмендегі теңдеумен анықталады:

(1)

мұндағы — адиабата көрсеткіші ( сутегі екі атомды газ үшін =1,4).

Осы теңдеуден Т₂ температураны өрнектейміз :

(2)

Берілген шамалардың мәндеріе (2) ге қойып ,

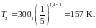анықтаймыз.

Адиабаталық ұлғаю соңындағы А газдың атқарған жұмысы

: (3)

формуласымен есептеледі. (3) ге шамалардың мәндерін қойып:

29,8 кДж.

аламыз.

Газдың изотермиялық сығылужұмысы А₂ :

(4.4.3.4) фопмуласымен есептеледі.

(4) формула бойынша есептеу жүргіземіз: А₂= - 21 кДж. Мұндағы «- »

таңбасы сыртқы күштердің жұмыс атқарғанын анықтайды.

Барлық процестердегі толық жұмыс:

29,8 + (— 21) = 8,8 кДж.

№5.191; №5.193; №5.195; №5.197. (Волкенштейн В.С. Жалпы физика курсының есептер жинағы., Алматы, Мектеп, 1974) есептерді шығарыңыздар

Тақырып: Термодинамиканың екініші бастамасы

1- есеп

Массы 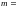100 г =0 °С температурадағы су t₂= 100 °С ге қыздырылып сол температурада буға айналды. Суды қыздыру кезіндегі S энтропия өзгерісін анықтаңдар. Судың меншікті жылу сиымдылығы 4200 Дж/(К∙кг), меншікті булану жылуы 2,25∙10⁶ Дж/кг ге тең.

Шешуі.

Қыздырылу және булану кезіндегі энтропия өзгерістерін жеке –жеке анықтаймыз.Энтропияның толық өзгерісі олардың қосындысына тең болады.

Энтропия өзгерісі

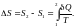формуласымен есептеледі (1)

Температураның 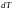өзгерісіндегі денеге берілетін жылу мөлшері δQ=mc•dT, мұндағы - дененің массасы ; с — оның меншікті жылу сиымдылығы . δQ өрнегін формуласына қойып суды қыздыру кезіндегі энтро­пия өзгерісін есептейтін формуланы аламыз:

(2)

Тұрақтыларды интеграл таңбасының алдына шығарып және интегралдау жүргізіп

теңдеуін аламыз. (3)

После подстановки численных значений и вычислений найдем

= 132 Дж/К.

При вычислении изменения энтропии во время превращения воды в пар той же температуры (фазовый переход первого рода есть изотермический процесс) можно вынести за знак интеграла постоянную температуpу T. Тогда, вычислив интеграл, найдем

(4)

где Q — количество теплоты, переданное при превращении нагре­той воды в пар той же температуры.

Подставив в формулу (4) выражение для количества теплоты, необходимое для фазового перехода I рода (превращение воды в пар),

Q= , (5)

где — удельная теплота парообразования, получим

(6)

Произведя вычисления по формуле (6), найдем: 605 Дж/К.

Полное изменение энтропии при нагревании воды и последую­щем превращении ее в пар равно =737 Дж/К.

2- есеп

Шешуі.

№5.201; №5.203; №5.205; №5.207. (Волкенштейн В.С. Жалпы физика курсының есептер жинағы., Алматы, Мектеп, 1974) есептерді шығарыңыздар

Тақырып: Реал газдар (1 сағ)

Негізгі сұрақтар:

1. Ван-дер-Ваальс теңдеуі

2. Ван-дер-Ваальс изотермалары

3. эксперименттік изотермалар

4. реал газдың ішкі энергиясы

5. Джоуль-Томсон эффектісі

6. газдарды сығу

Молекулалардың меншікті көлемін ескеру

Бір моль идеал газ үшін жазылған Менделеев-Клапейрон теңдеуіндегі – 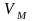қозғалыстағы молекулаға берілген ыдыс көлемі. Нақты газ үшін осы көлемнің кейбір бөлігін молекулалардың өздері алады. Сондықтан нақты газ молекулаларына шын мәнінде берілген көлем –дан кем және 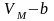–ға тең. Сонда

(14.1)

Теориялық есептеулерге сәйкес бір моль газ молекулаларының өздері алып жатқан көлемі жуықтап алғанда сол молекулалардың төрт еселенген меншікті көлеміне тең: