Экстремум в экономике

Математические методы широко используются в таких вопросах, как планирование народного хозяйства, организация управления, планирование военных операций и т.д. Задачи управления и планирования обычно сводятся к выбору некоторой системы числовых параметров или функции, обеспечивающих наиболее эффективное достижение поставленной цели (оптимальный план) с учётом ограниченности возможных ресурсов. Слово оптимальный происходит от латинского слова optimum – наилучший.

Для оценки эффективности плана вводится так называемая целевая функция (показатель качества плана), выраженная через характеристики плана и принимающая экстремальные значения (наименьшее или наибольшее значения) для оптимального плана.

Задачи оптимизации бывают линейные и нелинейные.

Нелинейные задачи оптимизации решают методами классического анализа. В научных исследованиях и производственных испытаниях результаты опытов чаще всего изображаются в виде таблиц и графиков. Полученные опытные данные обычно подвергают математической обработке, выражая их с помощью формулы с точностью, не превышающей определённой погрешности. Полученная при этом функция имеет ограничения, отражающие условия производства и особенности динамики процессов. В интересах производства важно знать такие значения независимой переменой, при которых производственная функция принимает наибольшее или наименьшее значение.

Задача. Решёткой длиной 120 м. нужно огородить прилегающую к дому прямоугольную площадку наибольшей площади. Определить размеры прямоугольной площадки.

Решение: Обозначим через одну из сторон прямоугольной площадки. Тогда другая сторона будет равна

А площадь прямоугольной площадки будет равна

Тогда

;

- точка максимума.

Следовательно, размеры площади должны быть 30 х 60 м, тогда площадь прилегающего участка будет наибольшей, равной 1800 м².

Примеры решения задач

Задача. Вычислить пределы: а) , б) ,

в) , г) .

Решение.

а) .

Подстановка предельного значения аргумента х = -3 приводит к неопределенному выражению вида Для устранения этой неопределенности разложим числитель и знаменатель дроби на множители и сократим дробь на множитель (х + 3):

б)

При х → ∞ выражение дает неопределенность ∞ - ∞. Для ее устранения умножим и разделим это выражение на :

в)

Обозначим arctg 5x = y. Тогда 5х = tg y т у→0 при х→0. Применяя свойства пределов и формулу первого замечательного предела , имеем:

г)

При х→∞ выражение является неопределенностью вида 1^∞. Для устранения этой неопределенности представим основные степени в виде суммы 1 и бесконечно малой при х→∞ величины и применим формулу второго замечательного предела: . Тогда имеем:

Пусть 2х + 1 = -4у. Тогда 4х + 5 =-8у + 3 и у→∞ при х→∞.

Переходя к переменной у, получим:

Задача. Найти производные функции: а) , б) , в)

Решение.

а)

Последовательно применяя правила дифференцирования сложной функции, правила и формулы дифференцирования, имеем:

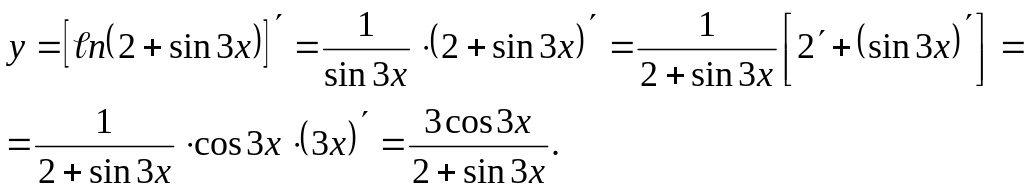
б)

в)

В данном случае функциональная зависимость задана в неявном виде. Для нахождения производной нужно продифференцировать по переменной х обе части уравнения, считая при этом у функцией от х, а затем полученное уравнение разрешить относительно :

Задача. Исследовать функцию и построить ее график.

Решение. Исследование функции проводим по следующей схеме:

1. Найти область определения функции.

2. Исследовать функцию на непрерывность.

3. Установить, является ли заданная функция четной, нечетной.

4. Найти интервалы возрастания и убывания функции и точки экстремума.

5. Найти интервалы выпуклости и вогнутости кривой и точки ее перегиба.

6. Найти асимптоты кривой.

Реализуем указанную схему.

1. Функция определена при всех значениях аргумента х, кроме х = 1.

2. Данная функция является элементарной, поэтому она непрерывна на своей области определения, т.е. на интервале (-∞; 1) и (1; +∞).

В точке х = 1 функция терпит разрыв второго рода.

3. Для установления четности или нечетности функции проверим выполнимость равенств (тогда - четная функция) или ( для нечетной функции) для любых х и –х из области определения функции:

Следовательно, и , то есть данная функция не является ни четной, ни нечетной.

4. Для исследования функции на экстремум найдем ее первую производную:

при х = 0 и не существует при х = 1.

Тем самым имеем две критические точки: х₁ = 0 и х₂ = 1.

Но точка х₂ = 1 не принадлежит области определения функции, экстремума в ней быть не может.

Разобьем числовую ось на 3 интервала: , и .

Найдем знак производной в каждом интервале.

В первом и третьем интервалах производная функции отрицательна, следовательно здесь функция убывает; во втором интервале – положительна и данная функция возрастает.

При переходе через точку х = 0 первая производная меняет свой знак с минуса на плюс, поэтому в этой точке функция имеет минимум: . Значит, А(0; -1) – точка минимума.

5. Для определения точек перегиба графика функции и интервалов выпуклости и вогнутости кривой найдем вторую производную: при и - не существует при х = 1. Разобьем числовую ось на три интервала: На первом интервале вторая производная отрицательна и дуга исследуемой кривой выпукла; на втором и третьем интервалах > 0, тем самым график является вогнутым. При переходе через точку , меняет свой знак, поэтому - абсцисса точки перегиба. Следовательно, В точка перегиба графика функции.

6. x = 1 – точка разрыва функции, причем . Поэтому прямая х = 1 является вертикальной асимптотой графика.

Для определения уравнения наклонной асимптоты воспользуемся формулами: .

Тогда , .

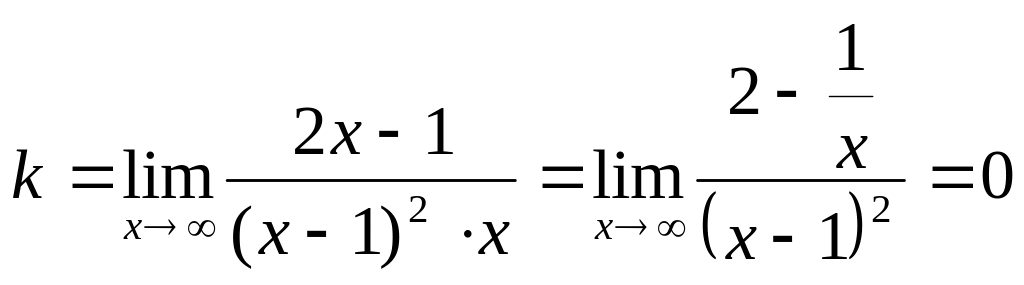Значит, прямая у = 0 есть горизонтальная асимптота графика исследуемой функции, представленного на рисунке

Задача. Резервуар, имеющий форму открытого сверху прямоугольного параллелепипеда с квадратным дном, нужно вылудить внутри оловом. Каковы должны быть размеры резервуара при его емкости 108 л. воды, чтобы затраты на его лужение были наименьшими?

Решение. Затраты на покрытие резервуара оловом будут наименьшими, если при данной вместимости его поверхность будет минимальной.

Обозначим через а_дм – сторону основания, b_дм – высоту резервуара. Тогда площадь S его поверхности равна а объем

Отсюда и

Полученное соотношение устанавливает зависимость между площадью поверхности резервуара S (функция) и стороной основания а (аргумент).

Исследуем функцию S на экстремум.

Найдем первую производную , приравняем ее к нулю и решим полученное уравнение:

Отсюда а = 6. (а) > 0 при а > 6, (а) < 0 при а < 6.

Следовательно, при а = 6 функция S имеет минимум. Если а = 6, то b = 3.

Таким образом, затраты на лужение резервуара емкостью 108 литров будут наименьшими, если он имеет размеры 6дм х 6дм х 3дм.