7.3 Определение усилий, возникающих в сечениях ригеля от действия внешней нагрузки

Ригель рассматриваем как свободно опёртую балку с максимальным моментом в середине пролёта, опорами для которой служат колонны, а крайними – стены. При расчёте делаем два сечения: по длине ригеля в зоне максимального момента и на опоре в зоне подрезки.

Значение максимального изгибающего момента в сечении ригеля вычислим по формуле:

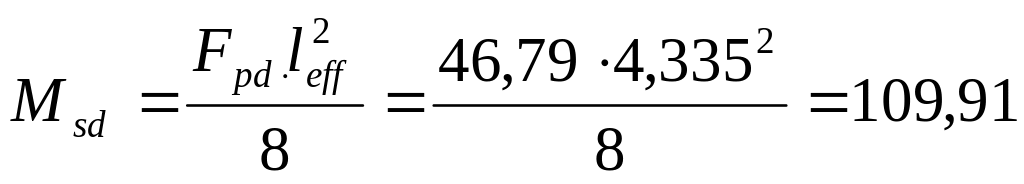кН/м (7.2)

Значение поперечных сил на промежуточных опорах:

кН (7.3)

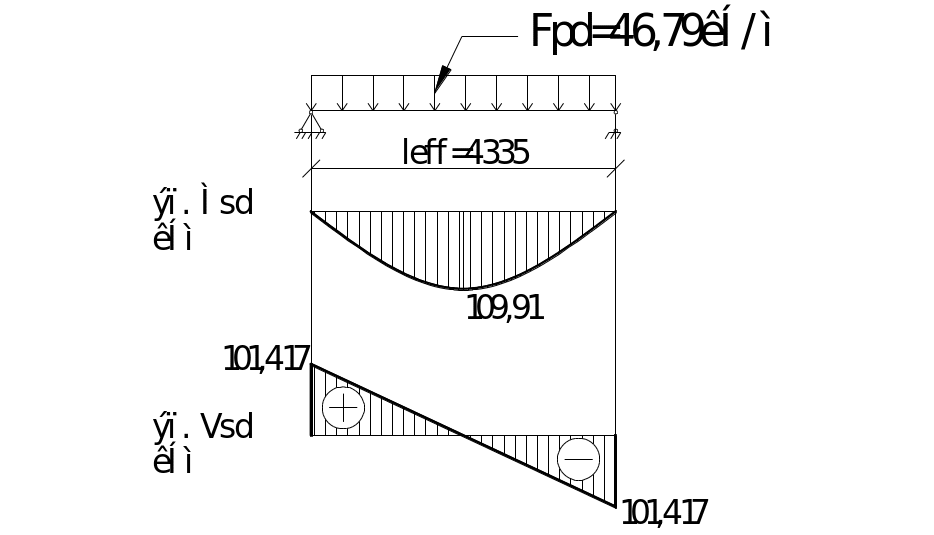
Рисунок 14 – Расчётная схема ригеля.

7.4 Расчет прочности нормальных сечений ригеля

Проверку достаточности принятых размеров ригеля выполняем по значению изгибающего момента в пролете. Рабочая высота сечения

ширина ригеля

Значение коэффициента определяем по формуле:

где - коэффициент, учитывающий длительность действия нагрузки, неблагоприятного способа её приложения;

- расчётное сопротивление бетона сжатию;

– нормативное сопротивление бетона осевому сжатию;

- частный коэффициент безопасности для бетона;

Значение коэффициента :

, следовательно, сжатая арматура по расчету не требуется.

Для арматуры S500 МПа,

Определяем граничную относительную высоту сжатой зоны бетона :

где w – характеристика сжатой зоны бетона, определяемая

где - коэффициент, принимаемый для тяжёлого бетона 0,85;

- напряжения в арматуре, Н/мм², принимаемые для арматуры S500 равными

- предельное напряжение в арматуре сжатой зоны сечения, принимаемое 500 Н/мм²;

.

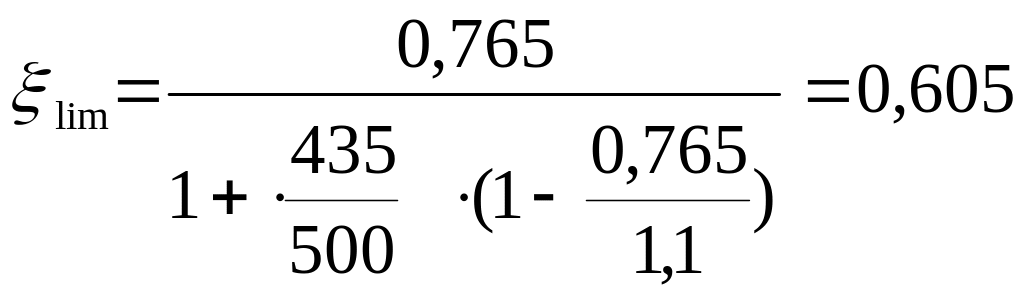
Определяем относительную высоту сжатой зоны бетона по формуле:

следовательно, растянутая арматура достигла предельных деформаций.

Требуемая площадь сечения растянутой арматуры, по формуле:

Принимаем 2Æ20 и 1Æ14 S500. Принятая площадь сечения

7.4 Расчёт прочности сечений наклонных к продольной оси ригеля

Расчет ведем аналогично расчету второстепенной балки.

Прочность железобетонной балки на действие поперечной силы определяем, в первую очередь, проверкой условия:

(3.11)

Определим значение поперечной силы, воспринимаемой сечением без поперечного армирования:

,но не менее (3.12)

где , d — в мм; , т.е. подставляем максимальное значение 1,7;

< 0,02 (минимальное значение коэффициента армиро­вания, регламентированное СНБ 5.03.01).

Тогда расчетный коэффициент армирования

Тогда, с учетом рассчитанных величин получим:

Условие не выполняется, тогда используя метод ферменной аналогии, поперечное армирование определим из условий и

Зададимся углом наклона трещин к горизонтали и шагом поперечной арматуры S=150мм.

Где Z-расстояние между равнодействующими в сечении:

Принимаем 2 стержня диаметром 10мм класса S500 (A_sw=157 мм²) c шагом S=150мм.

При этом должны выполняться условия:

(3.13)

(3.14)

-условие выполняется, прочность по сжатой полосе обеспечена.

-условие выполняется, что означает оптимальности принятого армирования.