Математичний аналіз
Теоретичні питання
Означення скінченних та нескінченних границь числових послідовностей. Поняття збіжної послідовності. Властивості границь послідовностей.
Означення границі функції однієї змінної за Гейне і за Коші. Неперервні функції в точці та на множині. Властивості неперервних на відрізку функцій.
Похідна функції однієї змінної, її фізичний та геометричний зміст. Правила знаходження похідних і таблиця похідних основних елементарних функцій.
Інтеграл Ньютона-Лейбніца, його механічний зміст та властивості.
Інтеграл Рімана та його геометричний зміст.
Поняття диференційованості функцій декількох змінних. Властивості диференційованих функцій. Достатня умова диференційованості.
Поняття збіжності та суми числового ряду. Абсолютно збіжні ряди та їх властивості.
Степеневі ряди, їх центри та коефіцієнти. Інтервал та область збіжності степеневого ряду.
Ряд Тейлора, достатня умова його збіжності. Приклади розкладу екстремальних функцій у ряди Тейлора.
Ряди Фур’є за тригонометричною послідовністю.
Практична частина
Зробити повне дослідження та побудувати графік функції
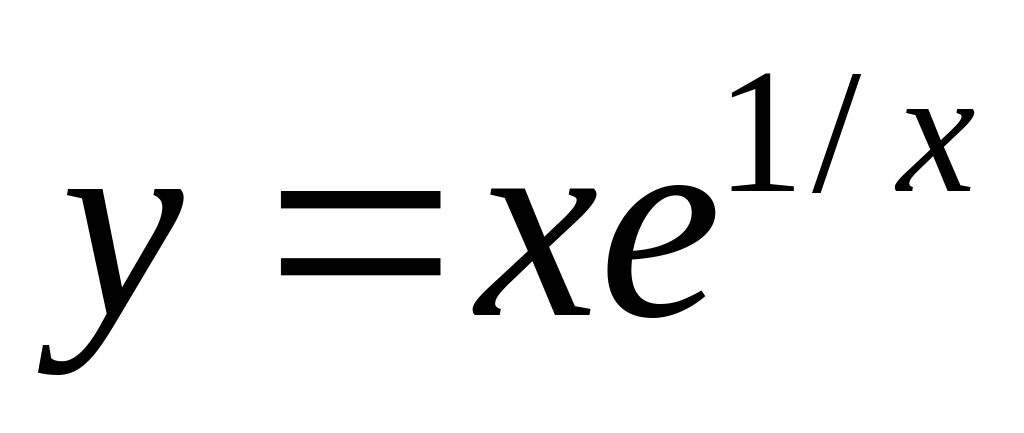.Яким має бути співвідношення між висотою та діаметром консервної банки, щоб на її виготовлення пішла найменша кількість матеріалу?
Переріз зрошувального каналу має форму рівнобічної трапеції, бокові сторони якої дорівнюють меншій основі. Яким має біти кут нахилу бокових сторін, щоб площа перерізу була найбільшою.
Знайти площу фігури, обмеженої лініями
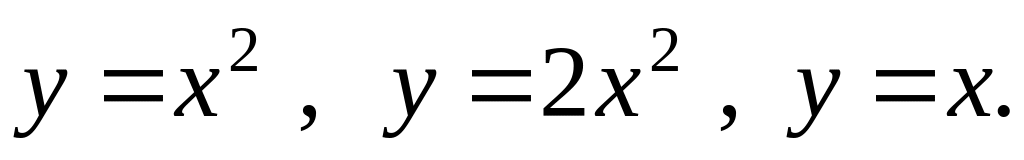
Знайти найменше та найбільше значення функції
на множині
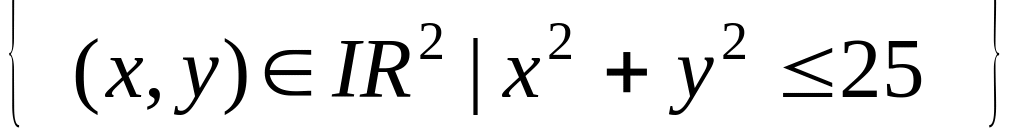.Дослідити на локальний екстремум функцію
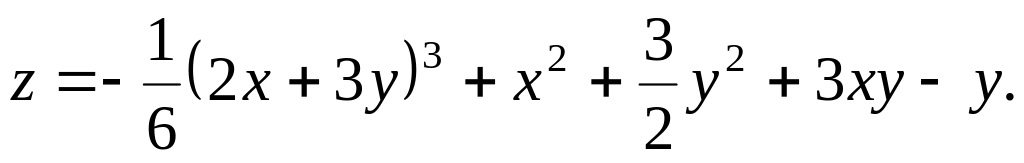
Наближено обчислити
з точністю до
Знайти площу поверхні
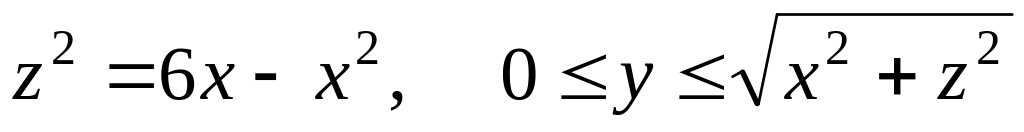.Розкласти функцію
в ряд Фур’є за синусами.Довести, що функція
- абсолютно інтегрована і знайти її
перетворення Фур’є.