Бази даних та інформаційні системи Теоретичні питання

1. Дати визначення поняттям:база даних,.СКБД, предметної області.

2. Основні групи користувачів бази даних.

3. Що таке генератор? Приклади використання.

4. Індексні файли та їх використання.

5. Дати визначення транзакції.

6. Що таке нормалізація? Описати нормальні форми з 1-ї по 5-ту

7. Перелічити основні операції реляційної алгебри

8. Функції адміністратора баз даних.

9. Що таке цілісність даних? Як підтримується цілісність даних?

10. Процедури, що збережені на сервері. Приклади використання.

Практична частина

База даних складається з 4-х таблиць

1. Записати оператори створення таблиць

2. Записати оператори створення ключів та зв’язків між таблицями

3. Використовуючи оператор INSERT ? додати новий запис в таблицю STUDENT

4. Використовуючи оператор DELETE знищити запис в таблицю VUKLAD

5. Вивести на екран прізвища, імена та розмір стипендії всіх студентів. Дані відсортувати в алфавітному порядку по прізвищах

6. Вивести список викладачів, прізвища яких починаються на літеру „Б”.

7. Вивести прізвища викладачів і назви предметів, які вони викладають.

8. Вивести інформацію про студентів, які мають 4 і 5 по певному предмету.

9. Вивести прізвища студентів і назви предметів, іспити з яких вони повинні скласти

10. Вивести прізвища студентів, що мають незадовільні оцінки

Алгебра та геометрія

Теоретичні питання

1. Означення визначника n-го порядку. Властивості визначників. Властивість Лапласа. Застосування визначників для розв’язування СЛАР.

2. Означення лінійного простору, приклади. Лінійна комбінація, лінійна залежність та незалежність елементів простору, лінійна оболонка елементів. Означення базису та розмірності лінійного простору. Координати елементів в даному базисі, їх властивості. Простір n-елементних векторів, його розмірність.

3. Означення матриці. Лінійні операції та множення матриць. Властивості цих операцій. Обернена матриця. Матричний метод розв’язання систем.

4. Ранг матриці. Знаходження рангу матриці методом елементарних перетворень. Метод Гауса розв’язування систем. Теорема Кронекера-Капеллі.

5. Скалярний добуток векторів. Властивості, фізичний зміст та застосування. Векторний та змішаний добутки векторів. Їх властивості та застосування.

6. Різні види рівняння прямої на площині. Рівняння площини та прямої в просторі. Основні задачі з ними.

7. Основна теорема алгебри. Ділення многочлена на многочлен з остачею. Теорема Безу. Розклад многочлена на множники в множинах комплексних та дійсних чисел.

8. Евклідовий простір. Приклади. Нерівність Коші-Буняковського. Довжина вектора, кут між векторами, проекція вектора на вектор. Ортогональність. Метод ортогоналізації Гільберта-Шмідта.

9. Лінійний оператор в скінченновимірних просторах. Матриця оператора в заданих базисах. Власні числа та власні вектори оператора (матриці). Алгоритм їх знаходження.

10. Квадратичні форми. Зведення квадратичної форми до канонічного вигляду. Закон інерції квадратичних форм. Достатня та від’ємна визначеність, критерій Сильвестра.

Практичні питання

1. Розв’язати однорідну СЛАР та знайти фундаментальну систему розв’язків.

2. Виконати дії з даними матрицями А,В,С, наприклад , С^-1(А^т-2В).

3. Скласти рівняння спільного перпендикуляра до двох мимобіжних прямих чи перейти від загальних рівнянь прямої в просторі до канонічних та параметричних.

4. Назвати криві (чи поверхні) та зобразити область, обмежену ними.

5. Добути всі комплексні корені і зобразити їх в комплексній площині .

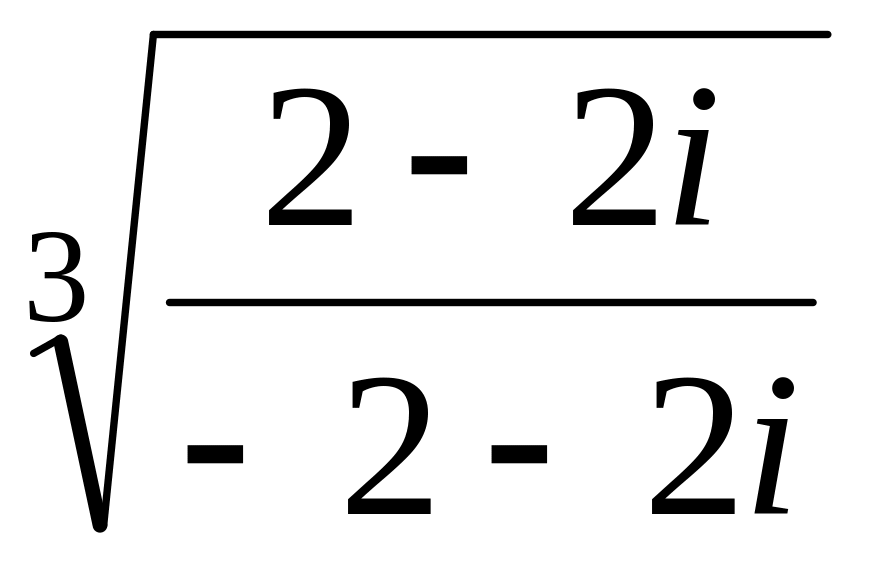6. Розкласти многочлен третього степеня на множники в множинах комплексних та дійсних чисел.

7. Знайти НСД двох многочленів.

8. Знайти матрицю оператора в іншому базисі.

9. Знайти власні числа та власні вектори матриці.

10. Звести загальне рівняння кривої другого порядку до канонічного. Зобразити криву в старій та новій системах координат.