Основні поняття. Теореми.

3. Означення: диференціальним рівнянням називається рівняння, що пов’язує незалежну змінну

, шукану функцію та її похідні .

Символічно диференціальні рівняння можна записати так або . Якщо шукана функція є функція однієї незалежної змінної, то диференціальне рівняння називається звичайним.

Означення: порядком диференціального рівняння називають порядок найвищої похідної, що входить у рівняння.

Означення: розв’язком диференціального рівняння наз. будь-яка функція така, що при підставці її у дане рівняння, вона перетворює його в тотожність.

Означення: загальним розв’язком диференціального рівняння 1-го порядку наз. функція , яка залежить від однієї довільної сталої і задовольняє наступнім умовам:

а) вона задовольняє диференціальне рівняння при будь-якому конкретному значенні сталої С;

б) яка б не була початкова умова при , тобто , можна знайти таке значення , що функція , задовольняє дану початкову умову. При цьому зауважимо, що значення належать до тієї області зміни змінних і , в якій виконуються умови теореми існування і єдності розв’язку.

У процесі пошуку загального розв’язку диференціального рівняння ми часто приходимо до співвідношення виду , яке нерозв’язне відносно . Вирішивши його відносно , отримуємо загальний розв’язок. Але виразити у в елементарних функціях не завжди вдається; в таких випадках загальний розв’язок залишається в неявному вигляді.

Рівність виду ,що задає неявно загальний розв’язок, наз. загальним інтегралом диференціального рівняння.

Означення: частинним розв’язком наз. довільна функція ,яка отримується із загального розв’язку ,якщо в ньому довільній сталій надати визначене значення . Співвідношення називається в цьому випадку частинним інтегралом. Дамо геометричну інтерпретацію диференціального рівняння 1-го порядку. Нехай дано диференціальне рівняння, розв’язане відносно пропорції: і нехай є загальний розв’язок даного рівняння. Цей загальний розв’язок визначає сімейство інтегральних кривих на площині Оху. Дане рівняння для кожної точки Мз коефіцієнтами х та у визначає значення похідної , тобто кутовий коефіцієнт дотичної до інтегральної кривої, що проходить через цю точку. Таким чином, дане диференціальне рівняння дає сукупність напрямків або, як кажуть, визначає поле напрямків на площині Оху. Отже, з геометричної точки зору задача інтегрування диференціального рівняння заклечається в знаходженні кривих, напрям дотичних до яких співпадає з напрямком поля у відповідних точках. Для диференціального рівняння геометричне місце точок, в яких виконується співвідношення , називають ізокліною, даного диференціального рівняння. При різних значеннях k отримуємо різні ізокліни. Рівняння ізокліни, що відповідає значенню k, буде, очевидно, . Побудувавши сімейство ізоклін, можна наближено побудувати сімейство інтегральних кривих. Кажуть, що знаючи ізокліни, можна якісно визначити положення інтегральних кривих на площині.

Накладемо деякі передумови на праву частину диференціального рівняння (1 порядку), та доведемо існування та єдність розв’язку, що визначається початковими даними. Перше доведення існування розв’язків диференціального рівняння належить Коші. Розглянемо доведення дане Пікаром; воно приводиться за допомогою методу послідовних наближень, який не тільки встановлює, що розв’язок існує, але й дає можливість обрахування.

Теорема: нехай дано диференціальне рівняння (1) і початкова умова ,при . (2) Нехай та неперервні в замкнутій області Д,

Д мал.1, тоді в деякому інтервалі (4) існує розв’язок рівняння (1), що задовольняє початкову умову (2); при цьому розв’язок єдиний. Число lбуде визначене нижче.

Доведення: спочатку розглянемо метод наближеного інтегрування диференціального рівняння. Використаємо при цьому теорію рядів. Інтегруючи члени рівняння (1) в межах від до і враховуючи, що , отримуємо . (5)

В останньому рівнянні шукана функція знаходиться під знаком інтегралу, і тому це рівняння називають інтегральним. Функція , що задовольняє рівняння (1) і початкові умови (2), задовольняє рівняння (5). Очевидно, що функція , що задовольняє рівняння (5), задовольняє рівняння (1) і початкові умови (2). Будемо вважати нульовим наближенням розв’язку. Підставляючи у підінтегральну функцію у правій частині рівності (5) замість у значення , отримаємо . (6)

Це є перше наближення розв’язку диференціального рівняння (1), що задовольняє умови (2). Підставляючи перше наближення у підінтегральну функцію у рівність (6), маємо (7).

Це друге наближення. Продовжуючи цей процес, маємо:

. . . . . . . . . . . . . . . . . . . . . . . . .

,

. . . . . . . . . . . . . . . . . . . . . . . . . . (8)

( )

( ) ( )

( )

З того, що і неперервні у замкненій області D, випливає, що існують такі сталі M>0 іN>0, що для всіх точок області виконуються співвідношення:

,(9) (10)

Число у рівності (4) – найменше з чисел а і , тобто . (11)

Застосуємо теорему Лагранжа до функції для двох довільних точок та , що належать області D:

, де , відповідно, . Тому для будь-яких двох точок виконується: .(12)

Повернемося до рівності (6). З неї з врахуванням (9), (4), (11) отримаємо . (13)

Таким чином, функція , визначена рівність (6) на відрізку (4), не виходить за межі області D.Перейдемо тепер до рівності (7). Аргументи функції не виходять із області D. Тому можна записати, що (14).

Методом повної індукції можна довести, що для будь-якого n виконується , якщо х належить інтервалу (4). Доведемо тепер, що існує границя , і функція у(х) задовольняє диференціальне рівняння (1) і початкову умову (2). Для доведення розглянемо ряд виду (17) з загальним членом , при цьому . Очевидно, що сума n+1 членів цього ряду рівна (18).

Оцінимо члени ряду (17) по абсолютній величині: (19).

На основі (6), (7) та (10) знаходимо (беремо знак +, якщо , і знак -, якщо ). Таким чином . (20)

Аналогічно з врахуванням (20) (21).

Продовживши так і далі, знайдемо: (22).

Таким чином для інтервалу функціональний ряд (17) мажорується. (Ряд називається мажорним, якщо кожен його член по абсолютній величині не більший відповідного члена деякого збіжного числового ряду з додатніми членами). Відповідний числовий ряд з додатніми членами, які більші за абсолютні величини відповідних членів ряду (17), буде (23) з загальним членом . Цей ряд збіжний, що легко перевірити, використавши ознаку Даламбера: . Таким чином ряд (17) мажорується, відповідно, він збіжний. Так як його члени є неперервні функції, то він збігається до неперервної функції у(х). Таким чином, ,(24) де у(х)- неперервна функція. Ця функція задовольняє початкову умову, так як для всіх n . Доведемо, що отримана функція у(х) задовольняє рівняння (1). Знову запишемо останнє із рівностей (8): (25)

Доведемо, що , (26) де у(х) визначена рівністю (24). Відмітимо, що оскільки ряд (17) мажорується, то із (24) слідує, що для будь-якого знайдеться таке ,що буде . (27)З урахуванням (27) на всьому інтервалі (4) можемо записати: . Але . Відповідно, . Із останньої рівності випливає рівність (26). Тепер, переходячи в обох частинах рівності (25) до границі при , отримаємо, що у(х), визначена рівність (24), задовольняє рівняння . (28)

Як вказувалося раніше, звідси випливає, що знайдена функція задовольняє диференціальне рівняння (1) і початкову умову (2). Тепер доведемо єдність даного розв’язку. Припустимо, що існує два розв’язки рівняння (1), задовольняючих умову (2), тобто дві криві, що виходять з точки . Відповідно, обидві ці функції задовольняють рівняння (28): Розглянемо різницю (29). Перетворимо підінтегральну різницю за формулою Лагранжа з врахуванням (10): (30). Із цієї рівності отримуємо: (31). На основі (29), з врахуванням (31), можна записати нерівність (32).

Розглянемо таке значення х, щоб . Для визначеності будемо вважати, що , для випадку доведення аналогічне.

Нехай найбільше значення на інтервалі набувається при і дорівнює . Тоді нерівність (32) для точки набуде вигляду або . За припущенням існування двох різних розв’язків прийшли до суперечності. Отже, розв’язок єдиний. Теорему доведено.

Зауваження 1: використовуючи інші методи доведення, можна стверджувати, що існує розв’язок рівняння (1), що задовольняє умову (2), якщо функція неперервна у області (теорема Пеано).

Зауваження 2: прийомом, аналогічними тому, яким було отримане співвідношення (22), можна показати, що похибка при заміні розв’язку його -м наближенням задається формулою .

Означення: рівняння виду , де - задані функції від або сталі, причому для всіх значень із тієї області, в якій ми його розглядаємо, називається лінійним диференціальним рівнянням другого порядку.

У подальшому будемо вважати, що функції неперервні при всіх значеннях , причому коефіцієнт . Якщо , то рівняння називається лінійним неоднорідним, якщо ж , то лінійно однорідним. Установимо деякі властивості лінійних однорідних рівнянь.

Теорема1: якщо та - два частинних розв’язки лінійного однорідного рівняння другого порядку (1) то є також розв’язок цього рівняння.

Доведення: так як і - розв’язки рівняння, тому (2). Підставляючи у рівняння (1) суму і використовуючи (2), будемо мати тобто є розв’язком рівняння.

Теорема 2: якщо - розв’язок рівняння (1) і - стала, то - теж розв’язок (1).

Доведення: підставляючи у рівняння(1) вираз , отримаємо теорему доведено.

Означення: два розв’язки рівняння (1) і називаються лінійно незалежними на відрізку , якщо їх співвідношення на цьому відрізку не є сталим.

Означення: якщо є функції від х, то визначник називається визначником Вронського або вронскіаном даних функцій.

Теорема: якщо функції і лінійно залежні на відрізку , то визначник Вронського на цьому відрізку тотожно рівний нулю.

Дійсно, якщо , де , то і

Теорема: якщо визначник Вронського складений для розв’язків і лінійного однорідного рівняння (1), не рівний нулю при якомусь значенні на відрізку , де коефіцієнти рівняння неперервні, то він не перетворюється в нуль ні при якому значенні на цьому відрізку.

Доведення: так як - розв’язки рівняння (1), то Домножимо члени першої рівності на 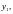а другої на і віднімемо, отримаємо

(3)

Тоді рівність (3) набуде вигляду:

(4). Знайдемо розв’язок рівняння (6), що задовольняє початкову умову Знайдемо спочатку загальний розв’язок рівняння (6), Відокремлюючи змінні, отримаємо , звідки ,звідси . (5)

Остання формула називається формулою Ліувіля. Розв’язок, що задовольняє початкові умови, прийме вигляд . ( )

За умовою , тоді із ( ) слідує, що .

Теорема: якщо розв’язки рівняння (3) лінійно незалежні на відрізку , то визначник Вронського , складений для цих розв’язків, не перетворюється в нуль в жодній точці вказаного відрізку.

Доведення: функція є розв’язком рівняння (1) на відрізку , що задовольняє початковим умовам , , де . Із теореми існування та єдності випливає, що не існує іншого розв’язку рівняння (1), що задовольняє початковим умовам; із цієї теореми випливає також, що якщо розв’язок рівняння(1) тотожній нуль на деякому відрізку чи інтервалі що належить , то цей розв’язок тотожно рівний нулю на всьому відрізку . Тепер припустимо, що в деякій точці відрізку . Тоді визначник Вронського буде рівний нулю і всіх точках відрізку : або Припустимо, що на , тоді можна записати, що або . Звідки слідує, що і - лінійно залежні, що суперечить умові. Далі припустимо, що в точках , що належать . Розглянемо інтервал , на ньому . Відповідно, на основі раніше доведеного, . Розглянемо функцію Ця функція є розв’язком рівняння (1) та на . Відповідно на відрізку або на , тобто та лінійно незалежні. Таким чином доведено, що вронскіан не перетворюється в нуль в жодній точці відрізку

Теорема: якщо та - лінійно незалежні розв’язки рівняння (1), то (6), де - довільні сталі, є його загальний розв’язок.

Доведення:якщо і - довільні, то за попередніми теоремами видно, що функція є розв’язком рівняння (1). Доведемо тепер, що при довільних початкових умовах можна підібрати і так, щоб відповідний частковий розв’язок задовольняв заданим початковим умовам. Підставляючи початкові умови у рівність (6) будемо мати ,(7) де

Із системи (7) можна визначити і , так як визначник цієї системи є визначник Вронського при і, відповідно не рівний нулю (в силу лінійної незалежності розв’язків і ). Частковий розв’язок, який отримано із сімейства (6) при знайдених значеннях та , задовольняє заданим початковим умовам.

Теорема: якщо відомо один частковий розв’язок лінійного однорідного рівняння другого порядку , то знаходження загального розв’язку зводиться до інтегрування функцій.

Зауваження: ця теорема дозволяє знаходити загальний розв’язок диференціального рівняння другого порядку з змінними коефіцієнтами, якщо відомий один його частинний розв’язок. Так як іноді вдається вгадати або знайти один частковий розв’язок безпосередньо, то ця теорема в багатьох випадках може виявитися корисною.