9. Построение переходных кривых в замкнутой аср по задающему и возмущающему воздействию методом Акульшина

Для автоматической системы регулирования с ПИ-регулятором:

Рисунок 14– Переходная кривая замкнутой АСР с ПИ-регулятором по задающему воздействию

Рисунок 15 – Переходная кривая замкнутой АСР с ПИ-регулятором по возмущению

Для автоматической системы регулирования с ПИД-регулятором:

Рисунок 16 – Переходная кривая замкнутой АСР с ПИД-регулятором по задающему воздействию

Рисунок 17 – Переходная кривая замкнутой АСР с ПИД-регулятором по возмущению

10. Анализ качества регулирования. Выбор наилучшего закона регулирования

Будем оценивать качество регулирования по прямым критериям, так как они позволяют оценивать качество непосредственно по переходной кривой. С помощью переходных кривых (см. рисунки 14 - 17) найдем прямые критерии качества и выберем наилучший закон регулирования.

1) Установившееся значение выхода, определяющее статическую точность системы

Находим, что для обоих законов регулирования .

2) Время переходного процесса, определяющее быстродействие системы (t_р ):

где примем 5% от , т.е. = 0,05.

Для кривой по задающему воздействию:

ПИ-регулятор: t_р=4,4 мин

ПИД-регулятор: t_р= 2,5 мин

3) Перерегулирование

Перерегулирование находится только для процесса по задающему воздействию, так как по возмущению h_уст=0:

ПИ-регулятор:

ПИД-регулятор:

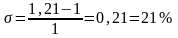
4) - частота колебаний:

_{ПИ - регулятор:}

ПИД - регулятор:

5) N - число полных колебаний, которое имеет h(t) за время регулирования t_р. Этот параметр определяется как число выбросов, для которых

Из графика переходных характеристик находим, что N = 0.

6) t_м - время достижения первого максимума.

ПИ-регулятор: t_м = 3,1 мин

ПИД-регулятор: t_м = 2,1 мин

7) t_н. - время нарастания переходного процесса, время от начала переходного процесса до момента первого пересечения графиком линии установившегося значения.

ПИ-регулятор: t_н = 2,2 мин

ПИД-регулятор: t_н = 1,5 мин

8) k - декремент затухания:

ПИ-регулятор:

ПИД-регулятор:

Оценим квадратичный интегральный критерий. Для этого для систем с ПИ и ПИД регуляторами введем дополнительную функцию:

, где

Рисунок 18 – График зависимости для системы с ПИ-регулятором

Рисунок 19 – График зависимости для системы с ПИД-регулятором

С помощью программного обеспечения MathCAD 14 найдем квадратичную интегральную оценку (интеграл решается методом трапеций):

ПИ-регулятор:

ПИД-регулятор:

Вывод: Вычисленная квадратичная интегральная оценка, характеризующая площадь под кривой квадрата динамической ошибки, позволяет сделать вывод, что для данного объекта регулирования наиболее подходящим является ПИД-регулятор с настроечными параметрами: ; ; .

ПИД-регуляторы обеспечивают наибольшее быстродействие систем при соблюдении оптимальных настроек, поэтому с увеличением запаздывания в системах резко возрастают отрицательные фазовые сдвиги, пропадает эффект дифференциальной составляющей, что в свою очередь ведет к изменению работы системы.

Литература

1. Г.К. Аязян «Определение параметров модели методом площадей Симою», Методическое руководство к курсовому и дипломному проектированию для студентов специальности «Автоматизация производственных процессов и производств», УГНТУ, Уфа, 2002

2. Г.К. Аязян «Пакет программ ТАУ кафедры АХТП УНГТУ», Краткое руководство пользователя, УГНТУ, Уфа, 1997

3. Г.К. Аязян «Расчет переходных процессов в системах управления методом Акульшина», Методическое руководство к курсовому и дипломному проектированию для студентов специальности «Автоматизация производственных процессов и производств», УГНТУ, Уфа, 2002

Изм.

Лист

№ докум.

Подп.

Дата

27

27

Лист