Задание №12

Цель работы: определить настройки типового регулятора (ПИ, ПИД, ПД), минимизирующие интегральный квадратичный критерий при заданном ограничении . Выбрать промышленный регулятор и его настройки.

Исходные данные:

Таблица 1 – кривая разгона

Время, мин.	Выходной сигнал (мм)
0,00	0
0,25	9
0,5	20
0,75	34
1,00	52
1,25	79
1,50	108
1,75	124
2,00	136
2,25	143
2,50	148
2,75	149,7
3,00	150

Ход работы

Построение переходной кривой по табличным данным

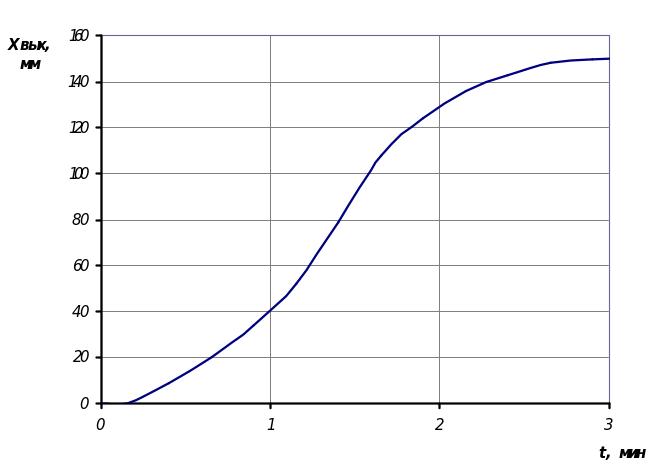
Рисунок 1 - Экспериментальная переходная кривая

На рисунке 1 приведена типичная кривая разгона объекта с самовыравниванием.

Определение параметров нескольких моделей объекта по переходной кривой методом «площадей» Симою

Коэффициент усиления K:

Введем в рассмотрение вспомогательную функцию , определяемую формулой:

, где

Моменты вспомогательной функции вычислим по формулам:

Для вычисления интегралов в формулах моментов воспользуемся методом трапеций. Согласно формуле трапеций интеграл вида,

заменяется суммой,

Получаем следующие формулы для вычисления моментов:

Таблица 2 – Расчет коэффициентов по методу «площадей» Симою

t, мин	, мм
0	0	1	0	0
0,25	9	0,94	-0,235	0,05875
0,5	20	0,867	-0,433	0,21667
0,75	34	0,773	-0,58	0,435
1	52	0,653	-0,653	0,65333
1,25	79	0,473	-0,592	0,73958
1,5	108	0,28	-0,42	0,63
1,75	124	0,173	-0,303	0,53083
2	136	0,093	-0,187	0,37333
2,25	143	0,047	-0,105	0,23625
2,5	148	0,013	-0,033	0,08333
2,75	149,7	0,002	-0,006	0,01513
3	150	0	0	0