
2.1.6. Производные основных элементарных функций
Производная логарифмической функции

По определению
производной
 Найдем приращение функции:
Найдем приращение функции:

Тогда, пользуясь
тем, что
 ~
~ при х0,
в силу следствия ко второму спецпределу
получим:
при х0,
в силу следствия ко второму спецпределу
получим:

Итак,
 .
В силу правила дифференцирования сложной
функции:
.
В силу правила дифференцирования сложной
функции:
 .
.
В частности ,
 .
.
2. Производная показательной функции y =ax.
По определению логарифмической функции функция y=ax имеет обратную x=logay.
Отсюда
 ,
,
то есть
 .
.
Для сложного
аргумента:
 .
.
В частности,
 .
.
Замечание. Формула для производной показательной функции легко может быть получена и непосредственно:

Производная степенной функции y=х.
Поскольку
- произвольно, будем считать, что х>0.
Тогда, логарифмируя равенство y=х,
получим lny=lnx.
Продифференцируем обе его части:
 .
.
Отсюда
 или
или

Итак
 .
.
Для сложного
аргумента
 .
.
Можно показать, что если показатель таков, что функция y=х определена и при х0 или х<0, то формула ее производной сохраняется и для этих значений х.
Замечание.
Метод, предложенный для нахождения
 ,
называют методом логарифмического
дифференцирования. Его применяют при
вычислении производных произведений,
частных, степенно-показательных
выражений.
,
называют методом логарифмического
дифференцирования. Его применяют при
вычислении производных произведений,
частных, степенно-показательных
выражений.
4. Производная функция y =s inx.
По определению производной:

 Таким
образом,
Таким
образом,
 .
.
Для сложного
аргумента

5. Производная функции y = cosx.
Аналогично
предыдущему легко получить
 а для сложного аргумента
а для сложного аргумента
 .
.
6. Производная функции y = tgx.
В силу формулы для
дифференцирования дроби имеем:

Итак,
 ,
,
 .
.
Производная функции y = ctgx.
Аналогично предыдущему легко проверить, что:
 ,
,
 .
.
Производная функции y = arcsinx.
По определению
функции
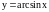 имеем:
имеем:
 .
.
Тогда
 .
.
Но
 .
Знак “+” перед корнем выбран по
определению функции arcsinx
(угол y
лежит в первой четверти). Таким образом,
.
Знак “+” перед корнем выбран по
определению функции arcsinx
(угол y
лежит в первой четверти). Таким образом,
 и, следовательно,
и, следовательно,
 .
.
Производная функции y = arccosx.
По определению
 ,
поэтому, дифференцируя обе части,
получим
,
поэтому, дифференцируя обе части,
получим
 .
.
Отсюда
 ,
а
,
а
 .
.
Производная функции y = arctgx.
Аналогично п.8 получим:
 .
.
Производная функции y = arcctgx.
Аналогично п.9 получаем:

