4. Расчёт мешающих влияний тяговой сети на линию связи

В соответствии с заданными параметрами, построим расчётную схему взаимного расположения тяговой сети и двухпроводной линии связи.

Рисунок 7 – Расчётная схема расположения тяговой сети и линии связи

Для воздушной и кабельной линии связи, имеющих одинаковое сближение с тяговой сетью и одинаковые трассы, необходимо определить напряжение шума, создаваемого за счёт влияния ряда гармоник тягового тока. Учитывается влияние гармоник с кратностью к = 1, 3, 5, …, 69 по отношению к основной частоте тока, равной 50 Гц.

Для расчёта напряжения мешающих влияний требуется определить гармонический состав тока контактной сети, используя заданную кривую полуволны тягового тока, то есть получить значения амплитуд синусоидальных составляющих кривой. Для этого воспользуемся графоаналитическим методом.

Разложим кривую тока на гармоники с кратностью к = 1, 3, 5, 7, 9, 11, для чего, по теореме Котельникова, участок оси абсцисс от 0 до 180 достаточно разделить на 12 равных частей.

Полуволна тягового тока представлена на рисунке 8.

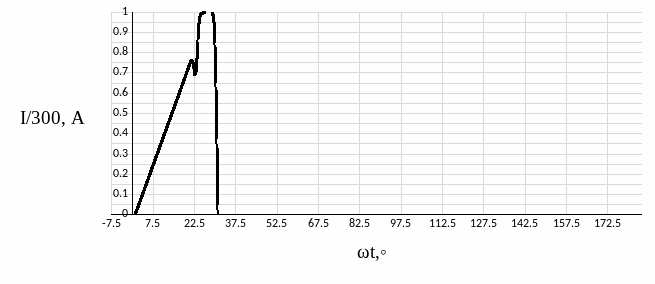
Рисунок 8 – Кривая полуволны тягового тока

Значения токов кривой, соответствующие серединам интервалов разбиения с номером i, определены графоаналитическим методом с помощью кривой полуволны тока, представленной на рисунке 8, и сведены в таблицу 1.

Таблица 1 - Значения токов середин интервалов разбиения

◦	7,5	22,5	37,5	52,5	67,5	82,5	97,5	112,5	127,5	142,5	157,5	172,5
I/300, A	0,56	0,7	0,71	0,75	0,81	0,86	0,91	0,95	0,98	1	0,98	0,66

В соответствии с теорией разложения периодических несинусоидальных функций, симметричных относительно оси абсцисс, в дискретный ряд Фурье рассчитываются амплитуды синусной 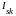и косинусной 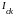составляющей -й гармоники ряда, А:

; (29)

, (30)

где − количество интервалов разбиения кривой полуволны тока по оси абсцисс, =12;

− значение тока кривой, соответствующее середине интервала разбиения с номером , А;

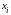− угол, соответствующий середине интервала с номером i,◦.

Амплитуда k-й гармоники:

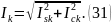
Начальная фаза k-й гармоники:

По формуле 29 рассчитаем (k=1):

По формуле 30 рассчитаем 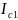(k=1):

По формуле 31 рассчитаем 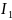(k=1):

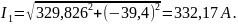
По формуле 32 рассчитаем (k=1):

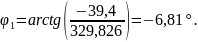
Остальные значения , , , сведём в таблицу 2.

Таблица 2 – результаты расчётов для построения гармоник тягового тока с кратностью 1…11

k	, A	, A	, A	, ○
1	329,826	-39,401	332,171	-6,812
3	97,604	13,620	98,55	7,944
5	54,356	9,279	55,142	9,687
7	34,488	5,044	34,855	8,32
9	23,973	2,395	24,093	5,704
11	20,171	1,013	20,196	2,875

На основании данных таблицы 2 построим гармоники тягового тока с кратностью 1…11, также их сумму и исходную полуволну тягового тока, изображённую на рисунке 8.

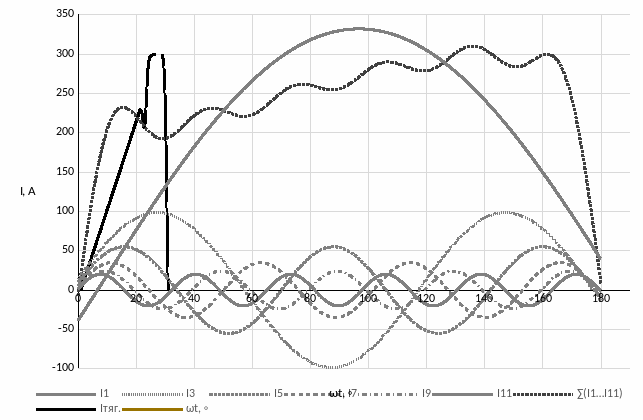Рисунок 9 – полуволна тягового тока и разложение её в ряд Фурье на гармоники с кратностью 1,3,5,7,9,11

35,97

Расчет напряжения шума в двухпроводной линии для каждой гармоники тока проводится по формуле 34, мВ:

, (32)

где – коэффициент акустического воздействия для -й гармоники;

– коэффициент чувствительности двухпроводной линии для - й гармоники.

Найдём напряжение шума для 1 – ой гармоники:

мВ.

Для других гармоник ряда расчеты производятся аналогично. Полученные данные сведены в таблицу №6.

Таблица №6 - Расчет напряжение шума в двухпроводной линии и напряжения шума в кабеле для 11 гармоник тока

Гармоника	Гн/км	,мВ	,мВ
1	0,000325	0,2586	0,0002
3	0,000223	11,189	0,010
5	0,000178	38,060	0,019
7	0,000151	48,949	0,052
9	0,000132	36,335	0,104
11	0,000118	34,914	0,063

Напряжение шума от воздействия всего спектра гармоник определяется с помощью формулы:

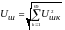. (33)

Произведем расчет этой величины:

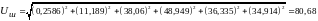мВ.

Необходимо рассчитать напряжение шума в кабеле, предполагая, что его трасса соответствует трассе воздушной линии связи. Тип кабеля МКБАБ 7х4х1,2+6х0,9. Расчет напряжения шума в кабеле -й гармоники проводится по формуле, мВ:

, (34)

где − коэффициент чувствительности двухпроводной кабельной линии;

– коэффициент экранирующего действия оболочки кабеля.

Определим напряжение шума в кабеле для 1-ой гармоники:

, мВ

Для других гармоник ряда расчеты производятся аналогично. Полученные данные сведены в таблицу №6.

Найдем напряжение шума в кабеле от первых 11 гармоник, мВ:

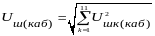(35)

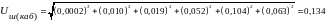мВ.

Амплитуды гармоник с кратностью =13, 15…….69 можно определить по справочной кривой путём умножения амплитуды тока первой гармоники 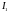на поправочный коэффициент .

Определяется напряжение магнитных влияний в одном проводе воздушной линии связи от тока каждой гармоники, рассчитывается напряжение шума в двухпроводной линии для каждой гармоники тока, напряжение шума от воздействия всего спектра гармоник. Также производится расчёт напряжения шума в кабеле для -й гармоники и напряжение шума в кабеле от воздействия всего спектра гармоник. Все расчёты для гармоник с 13 по 69 производятся аналогичным образом как и для первых 11. Результаты вычислений представлены в таблице №7.

Определим напряжение шума от воздействия всего спектра гармоник от 1 по 69:

А теперь определим напряжение шума в кабеле от всего спектра гармоник с 1 по 69:

Таблица №7 - Расчет напряжение шума в двухпроводной линии и напряжения шума в кабеле для гармоники тока с 13 по 69

Гармоника	Гн/км			,мВ	,мВ
13	0,000107	0,018	33,800	14,666	0,081
15	0,000098	0,017	38,107	17,387	0,100
17	0,000090	0,015	40,349	20,238	0,104
19	0,000084	0,013	39,579	20,288	0,097
21	0,000078	0,013	40,677	21,664	0,110
23	0,000073	0,012	41,024	23,589	0,108
25	0,000069	0,012	62,137	36,327	0,171
27	0,000065	0,011	75,656	45,625	0,193
29	0,000062	0,011	66,211	42,589	0,179
31	0,000059	0,01	20,912	13,632	0,051
33	0,000056	0,01	15,869	10,618	0,038
35	0,000054	0,009	13,023	9,214	0,028
37	0,000051	0,009	11,873	8,595	0,026
39	0,000049	0,009	10,800	8,017	0,023

Продолжение таблицы №7

41	0,000047	0,008	8,073	6,156	0,016
43	0,000046	0,008	7,526	5,905	0,015
45	0,000044	0,008	7,018	5,613	0,014
47	0,000042	0,007	6,458	5,290	0,011
49	0,000041	0,007	5,851	4,931	0,010
51	0,000040	0,007	5,258	4,527	0,009
53	0,000038	0,006	4,680	4,119	0,007
55	0,000037	0,006	4,096	3,686	0,006
57	0,000036	0,006	3,507	3,228	0,006
59	0,000035	0,005	2,967	2,787	0,004
61	0,000034	0,005	2,425	2,325	0,003
63	0,000033	0,005	1,927	1,878	0,003
65	0,000032	0,004	1,904	1,889	0,002
67	0,000031	0,004	1,904	1,916	0,002
69	0,000031	0,004	1,892	1,951	0,002