ДКР_інтеграли
.pdf
Варіант 3.
1. Обчислити інтеграл, користуючись таблицею і властивостями інтегралів.
∫3
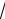x +2x2 −1dx 2x
2. Обчислити інтеграл за допомогою заміни змінної.
ex dx
∫
4 +e2 x
3.Обчислити інтеграл, використовуючи формулу інтегрування частинами.
∫(x +2) cos3xdx
4.Обчислити інтеграл з квадратним тричленом у знаменнику дробу.
∫ x +6 dx
3x2 + x +1
5.Обчислити інтеграл від тригонометричного виразу.
∫cos2 2x sin 2 2x dx
6.Обчислити інтеграл від тригонометричного виразу.
(3 +2tgx)dx
∫2sin 2 x +3cos2 x +1
7.Обчислити інтеграл від ірраціональної функції.
dx
∫3 
1 −3x − 
1 −3x
8. Обчислити інтеграл за допомогою тригонометричної підстановки.
∫ |
dx |
|
|
|
|
|
|
|
|
|
|
|
|
(25 + x2 ) |
3 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
∫2 |
(1− |
|
|
)3 |
|
π |
π |
|
|
|
|
|
.∫3 x sin xdx ; |
∫2 |
cos xdx |
|||||||
9. Обчислити інтеграли: |
|
x |
dx ; |
||||||||||
|
x |
1+cos x |
|||||||||||
|
|
|
|
|
1 |
|
|
0 |
0 |
||||
10. Обчислити площу фігури, обмеженої даними лініями у Декартовій системі координат: y=x2 , y= 2x .