6. Осуществить прогнозирование среднего значения показателя у при уровне значимости , если прогнозное значение фактора х увеличится на 20% от его среднего значения.

Согласно условию задачи прогнозное значение факторной переменной Х составит . Рассчитаем по уравнению модели прогнозное значение показателя У:

Таким образом, если среднедушевой прожиточный минимум на один день составит 98,073 рубля, то ожидаемое значение среднедневной зарплаты будет 132,85 рубля.

Зададим доверительную вероятность и построим доверительный прогнозный интервал для среднего значения Y.

Для этого нужно рассчитать стандартную ошибку прогнозирования

. (досчитать)

При размах доверительного интервала для среднего значения

Границами прогнозного интервала будут

;

Таким образом, с надёжностью в 90 % можно утверждать, что если среднедушевой прожиточный минимум на один день составит 98,51 рубля, то ожидаемая среднедневная заработная плата будет от 130,95 рублей, то 161,09 рублей.

7. Представить графически: фактические и модельные значения у, результаты прогнозирования.

8. Составить уравнения нелинейной регрессии: гиперболической, степенной, показательной. Привести графики построенных уравнений регрессии.

Для ее построения выполним линеаризацию: обозначим и получим вспомогательную модель Вспомогательная модель является линейной. Ее можно построить с помощью программы РЕГРЕССИЯ, предварительно подготовив исходные данные: столбец значений у_i (остается без изменений) и столбец преобразованных значений 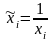(таблица 7).

Таблица 7

Y	Х	1/X
167	120	0,008333
126	86	0,011628
151	76	0,013158
144	70	0,014286
148	84	0,011905
150	88	0,011364
130	81	0,012346
147	81	0,012346
132	80	0,0125
149	80	0,0125
132	73	0,013699
119	72	0,013889
127	83	0,012048
129	90	0,011111
131	81	0,012346
120	88	0,011364
125	80	0,0125
122	78	0,012821
130	68	0,014706
143	84	0,011905
117	79	0,012658
152	84	0,011905