3. Проверить выполнение предпосылок мнк.

Предпосылками построения классической линейной регрессионной модели являются четыре условия, известные как условия Гаусса-Маркова.

1. В уравнении линейной модели слагаемое ε – случайная величина, которая выражает случайный характер результирующей переменной Y.

2. Математическое ожидание случайного члена в любом наблюдении равно нулю, а дисперсия постоянна.

3. Случайные члены для любых двух разных наблюдений независимы (некоррелированы).

4. Распределение случайного члена является нормальным.

1)Проведем проверку случайности остаточной компоненты по критерию поворотных точек.

Количество поворотных точек определим по графику остатков: p=16.

Вычислим критическое значение по формуле

. При 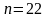найдем .

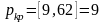Сравним p=16>p крит=9, следовательно, свойство случайности для ряда остатков выполняется.

2) Равенство нулю математического ожидания остаточной компоненты для линейной модели, коэффициенты которой определены по методу наименьших квадратов, выполняется автоматически.

С помощью функции СРЗНАЧ для ряда остатков можно проверить: .

Свойство постоянства дисперсии остаточной компоненты проверим по критерию Голдфельда-Квандта.

В упорядоченных по возрастанию переменной Х исходных данных ( ) выделим первые 8 и последние 8 уровней, средние 6 уровней не рассматриваем(четверть исключаем).

С помощью программы РЕГРЕССИЯ построим модель по первым восьми наблюдениям (регрессия-1), для этой модели остаточная сумма квадратов SS (1) = 1053,495

С помощью программы РЕГРЕССИЯ построим модель по последним восьми наблюдениям (регрессия-2), для этой модели остаточная сумма квадратов SS (2) = 731,3765.

Рассчитаем статистику критерия: .

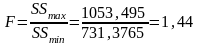Критическое значение при уровне значимости и числах степеней свободы 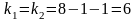составляет

Сравним 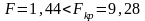, следовательно, свойство постоянства дисперсии остатков выполняется, модель гомоскедастичная

3) Для проверки независимости уровней ряда остатков используем критерий Дарбина-Уотсона

.

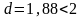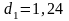Полученное значение , что свидетельствует о положительной корреляции. Перейдем к и сравним ее с двумя критическими уровнями и .

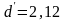не лежит в интервале от до 2, следовательно, свойство независимости остаточной компоненты не выполняется.

В учебных целях проверим выполнение свойства независимости ряда остатков по первому коэффициенту автокорреляции

.

.

Критическое значение для коэффициента автокорреляции определяется как отношение 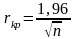и составляет для данной задачи .

Сравнение показывает, что 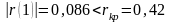, следовательно, ряд остатков некоррелирован.

4) Соответствие ряда остатков нормальному закону распределения проверим с помощью R/S – критерия

.

.

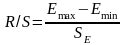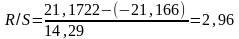Критический интервал определяется по таблице критических границ отношения R/S и при составляет

, значит, для построенной модели свойство нормального распределения остаточной компоненты не выполняется.

Проведенная проверка предпосылок регрессионного анализа показала, что для модели выполняются все условия Гаусса-Маркова , кроме последнего