Задание на курсовое проектирование

Задание 1

Определить основные свойства и характеристики потоков вызовов со следующими законами распределения интервалов между вызовами (интенсивность λ=6 выз/ч):

• простейший поток;

• распределение Эрланга;

• распределение Вейбулла;

• гамма распределение;

• распределение Парето;

Построить графики распределений. Построить совмещенный график распределений, при равном математическом ожидании интервала между вызовами потоков. Сравнить свойства потоков.

Задание 2

Для четырехзвенной коммутационной схемы блочной структуры (рис. 1), работающей в режиме группового искания, определить вероятность потерь методом вероятностных графов при следующих исходных данных (табл. 5):

Таблица 1 – Исходные данные к заданию 2

x	6
n	8
m	6
k	10
y,Эрл	0.35

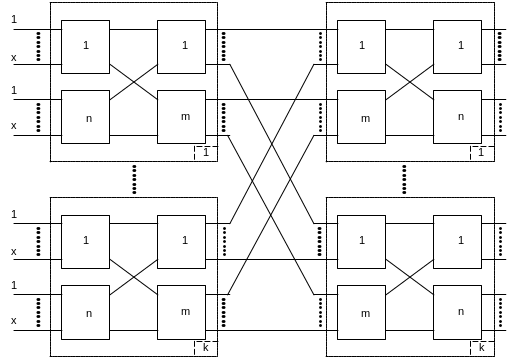
Рисунок 1. - Четырехзвенная коммутационная схема блочной структуры

Задание 3

По исходным данным произвести распределение интенсивности нагрузки от проектируемой АТС (узла коммутации) по заданным направлениям.

Таблица 2 – Исходные данные к заданию 3

Число пользователей	Точка подключения пользователей	Точка подключения АТС	Точка подключения провайдера интернет	Точка подключения оператора видеоуслуг
95	6	5	1	4
Вероятности блокировки доступа		0,001	0,005	0,01
Скорость передачи по каналам, кб/с		64	128	2000
c, выз/ч		-	12	4
, ч		-	0.1666	0.5
, Эрл		0.15	-	-
Коэффициент сжатия на первой ступени доступа к видеосерверу		8

Примечание:

- между узлами обслуживания 1-2-3-4 (3-6-7, 3-2-5-6) организованы каналы СЦИ; между 2-5 тракты ИКМ;

- между узлом доступа и АТС используются системы с ИКМ;

Содержание

Задание 1…………………………………………………………..…………....5

Задание 2……………………………………………………………………….13

Задание 3……………………………………………………………………….15

_{Список литературы……..………………………………………………………….17}

Задание 1

Потоком вызовов (в общем случае – событий) называется последовательность вызовов, поступающих через какие-либо интервалы или в какие-либо моменты времени.

Следует различать детерминированный и случайный потоки вызовов. Детерминированный поток вызовов – последовательность вызовов, в которой вызовы поступают в определенные, строго фиксированные неслучайные моменты или через определенные, строго фиксированные, неслучайные промежутки времени. Случайный поток вызовов отличается от детерминированного тем и только тем, что моменты поступления вызовов и промежутки времени между вызовами являются не строго фиксированными, а случайными величинами. Детерминированные потоки являются частным случаем случайных потоков и на практике встречаются редко.

Поток вызовов может быть определен тремя эквивалентными способами: последовательностью вызывающих моментов t₁, t₂,...,t_n, последовательностью промежутков времени между вызывающими моментами z₁, z₂,...,z_n и последовательностью чисел k₁, k₂,...,k_n, определяющих количество вызовов, поступающих в течение заданных отрезков времени [t₀, t₁), [t₀, t₂),..., [t₀, t_n). При этом под вызывающим моментом понимается момент одновременного поступления одного, двух и более вызовов; для вызывающих моментов всегда, если t_i>t_i-1, то z_i>0, в то время как для момента поступления вызова t_i.t_i-1 и z_i 0.

Для задания случайных потоков вызовов, как и любых других случайных величин и процессов, используются функции распределения. Функцией распределения вероятностей некоторой случайной величины X называется функция

определяющая вероятность того, что Х<х, где х – определенная, заданная величина.

Потоки вызовов подразделяются на неоднородные и однородные. Однородный поток вызовов характеризуется последовательностью, определяющей только закономерность поступления вызовов, т. е. последовательностью моментов поступления вызовов или промежутков времени между вызовами, либо иным способом задания потока вызовов.

В неоднородном потоке вызовов каждый вызов имеет две и более характеристики. Например, вызовы, поступающие от абонентов телефонной сети, определяются моментами их поступления, направлениями установления соединений, длительностью их обслуживания и другими характеристиками.

Стационарность потока. Поток вызовов является стационарным, если при любом n совместный закон распределения числа вызовов за промежутки времени [t₀, t₁), [t₀, t₂), ..., [t₀, t_n)

зависит только от длины промежутков времени и не зависит от момента t₀. Иными словами, независимо от того, где на оси времени расположен промежуток времени [t₀, t₁), вероятность поступления K(t₀, t_t) вызовов одна и та же. Это значит, что для стационарного потока вероятность поступления некоторого числа вызовов за какой-то промежуток времени зависит от длины этого промежутка и не зависит от его начала. В противном случае поток является нестационарным.

Ординарность потока. Обозначим через _k(t, t+) вероятность поступления k и более вызовов за промежуток [t, t+). Поток вызовов является ординарным, если при 0

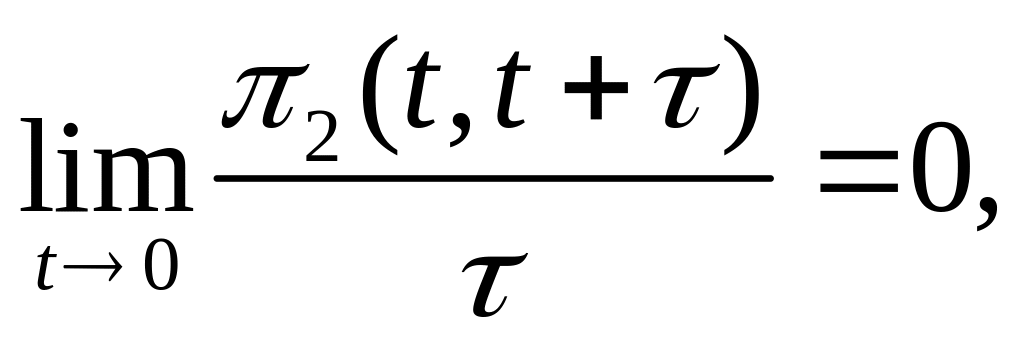
т. е. ₂(t, t+)=(), где ) – величина более высокого порядка малости по отношению к .

Ординарность потока выражает практическую невозможность одновременного поступления двух и более вызовов в любой момент времени t. Примером ординарного потока является поток вызовов, поступающий на телефонную станцию от абонентской группы любой емкости. Потоки телефонных вызовов к абонентам диспетчерской или конференц-связи, потоки телеграмм в несколько адресов являются неординарными.

Последействие потока. Поток вызовов является потоком без последействия, если вероятность поступления K(t₀, t_i) вызовов за промежутки

[t₀, t_i), i=1, 2, ..., n

не зависит от вероятностного процесса поступления вызовов до момента t₀. Иными словами, отсутствие последействия потока означает независимость течения случайного потока вызовов после какого-либо момента времени от его течения до этого момента. Примером потока без последействия может служить поток телефонных вызовов, поступающих от большой группы источников[2].

Рассмотрим простейший поток. Простейшим потоком называется стационарный ординарный поток без последействия. Функция плотности распределения интервалов между вызовами определяется формулой [1,2,3]:

,

где - интенсивность поступления вызовов, выз/ч

Математическое ожидание [1,2,3]:

Рисунок 1.1 – Функция плотности распределения интервалов между вызовами

Рассмотрим модель Эрланговского распределения. Функция плотности распределения интервалов между вызовами (1.2) определяется формулой [1,2,3]:

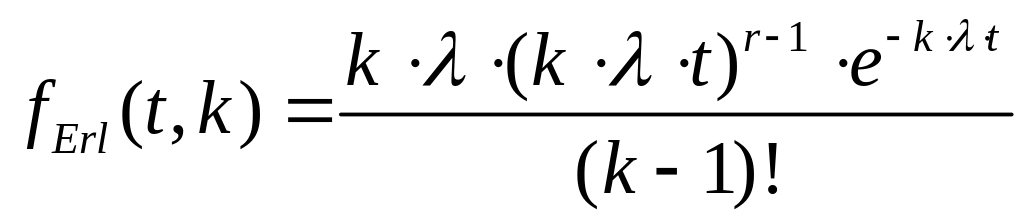
Где , параметр принимающий целые значения от 0 до ∞, k – также параметр распределения, для наглядности построим график функции при различных k.

Математическое ожидание [1,2,3]:

Рисунок 1.2 – Функция плотности распределения интервалов между вызовами

Рассмотрим гамма распределение. Функция плотности распределения интервалов между вызовами (рис.1.3) определяется формулой [1,3]:

,

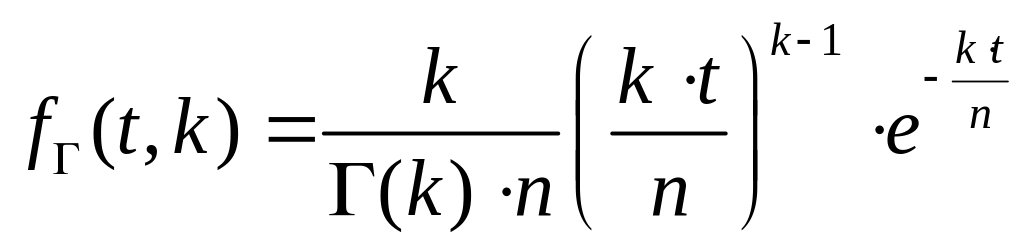где , - гамма функция, определяется как [1,3]:

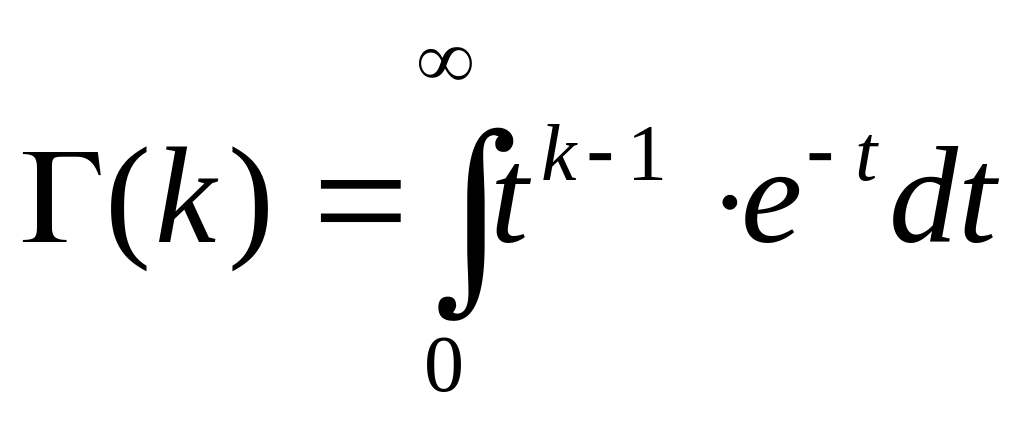
Математическое ожидание [1,3]:

Рисунок 1.3 – Функция плотности распределения интервалов между вызовами

Рассмотрим распределение Вейбулла. Функция плотности распределения интервалов между вызовами (рис.1.4) определяется формулой [1,3]:

Математическое ожидание [1,3]:

,

при .

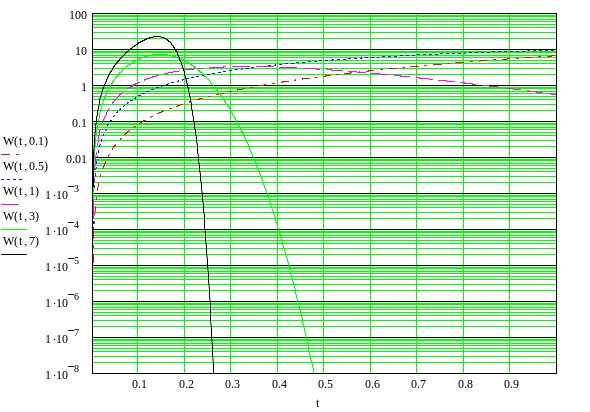
Рисунок 1.4 – Функция плотности распределения интервалов между вызовами

Рассмотрим распределение Парето. Функция плотности распределения интервалов между вызовами (рис.1.5) определяется формулой [1,3]:

,

,

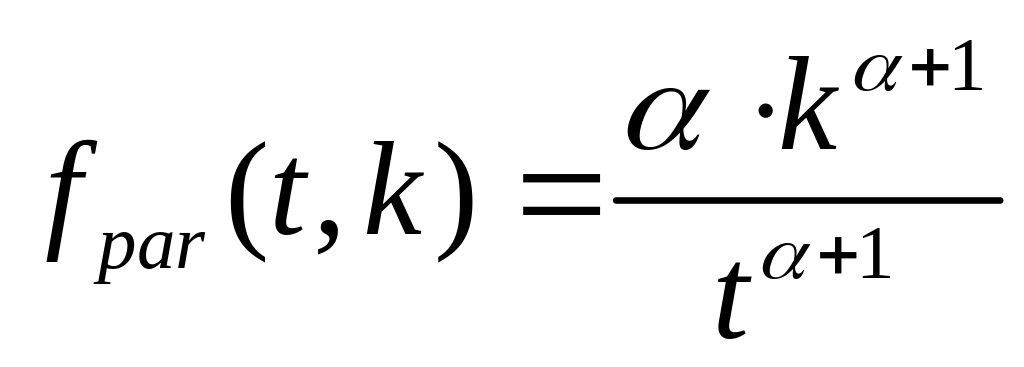где - коэффициент самоподобия ( ).

Математическое ожидание [1,3]:

,

при , .

Рисунок 1.5 – Функция плотности распределения интервалов между вызовами

Построим график сравнения функций распределения при равных значениях математического ожидания (рис.1.6).

Сравнив свойства рассмотренных потоков, отметим следующее: все виды распределений кроме распределения Парето, являются ординарными; все являются стационарными; показательное распределение без последействия, так же остальные распределения при тоже без последействия. При функции плотности распределений Вейбулла и Гамма обладают так называемым “тяжелым” хвостом – т.е. последействием. При наблюдается переход к детерминированному потоку для функций плотности распределений Вейбулла, Гамма и Эрланга.

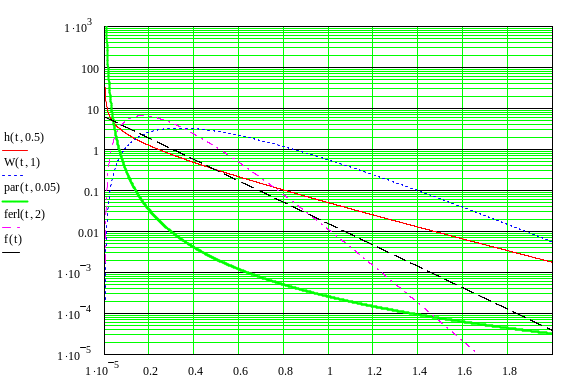
Рисунок 1.6 – Функция плотности распределения интервалов между вызовами.