Раздел 6. Расчет числа соединительных устройств и каналов в коммутационных системах с повторными вызовами.

6.1 Предварительные сведения

В настоящее время специалистами по системам распределения информации все более осознается необходимость учета поведения абонента (пользователя) при расчете пропускной способности системы. Наиболее известным «психологическим» фактором являются повторные попытки установить соединение. Однако в теории систем с повторными попытками получены только некоторые результаты. Сети связи до последнего времени рассчитывают на основе первой формулы Эрланга (для полнодоступного пучка) или ее модификации (для более сложных пучков), которая выведена при предположении, что абонент, получивший отказ в установлении требуемого ему соединения, забывает об этом и не делает повторных попыток. Однако на практике дело обстоит не так — потерянная попытка в большинстве случаев порождает повторные (рис. 6.1), что приводит к резкому несоответствию между проектными показателями, рассчитанными по формуле Эрланга, и результатами измерений на сети.

Рисунок 6.1 – Схема образования повторных попыток

При проектировании полнодоступных пучков обычно задается интенсивность поступающей нагрузки у и требуется выбрать такое число линий , чтобы потери по вызовам были не больше некоторого числа α ( ‰, 1% и т. п.), т. е. следует решить уравнение

, (6.1)

где – первая формула Эрланга

Ожидается, что среднее число занятых линий (интенсивность обслуженной нагрузки):

. (6.2)

При измерениях на сети из-за наличия повторных попыток оказывается, что отношение числа потерянных попыток (первичных и вторичных) ко всем поступившим попыткам многократно превосходит значение Е_υ(у). Обслуженная нагрузка также превышает запроектированную величину у_с. Эти расхождения иллюстрирует рис. 6.2а, где сравнивается Е₁₀(у) (пунктир) с кривыми вероятности потерь π₁₀(y,ν) при наличии повторных попыток (в случае абсолютно «настойчивого» абонента, т. е. производящего новую попытку после каждой потери при интенсивности повторений, равной ν). Так, при у=4,5 Эрл и ν=10 вместо значения Е₁₀(у)=0,01, ожидаемого согласно таблицам формулы Эрланга, наблюдается в среднем π=0,047, а вместо y_c=4,45 Эрл имеем 4,5. Если все же считать, как это делается сейчас в проектной практике, что наблюдаемое значение π=0,047 соответствует системе с потерями, то по таблицам формулы Эрланга находим, что такие потери были бы при нагрузке, равной 6,13 Эрл, Решением уравнения находим, что требуется υ′=12 линий. Однако это значение линий υ′ оказывается несколько завышенным, так как в системе с повторными попытками π₁₂(4,5; 10)≈0,008.

Ошибки в определении необходимого числа линий растут по мере роста нагрузки и допустимых потерь. Так, при планировании потерь в размере 0,1 находим, что допустимая поступающая нагрузка у = 7,5 (так как Е₁₀ (7,5) =0,1). Однако из-за повторных попыток наблюдаем π=0,6. Пользуясь таблицами Эрланга, находим, что для снижения потерь до значения 0,1 необходимо 25 линий.

Если же действительно предоставить такое число линий, то оно окажется явно завышенным, так как π₂₅(4,5; 10)<10^-8.Таблицы системы с повторными попытками показывают, что достаточно 14 линий (π₁₄(7,7; 10)≈0,07).

Использование оценок интенсивности обслуженной нагрузки дает меньшие ошибки. Так, при у=4,5 обслуженная нагрузка у_с=4,5 (все вызовы, в конце концов, обслуживаются). Следовательно, в рамках модели с потерями можем предполагать, что вместо Е₁₀(4,5)=0,01 имеем Е₁₀(4,5+0,01∙4,5)=0,011. Если у=7,5, то вместо Е₁₀(7,5)=0,1 имеем Е₁₀(7,5+0,1∙7,5)=Е₁₀(8,25)=0,133. Приведенные расчеты показывают, что формула Эрланга не дает удовлетворительного решения задачи определения числа линий в сетях связи, и теория расчета сетей должна быть кардинально пересмотрена.

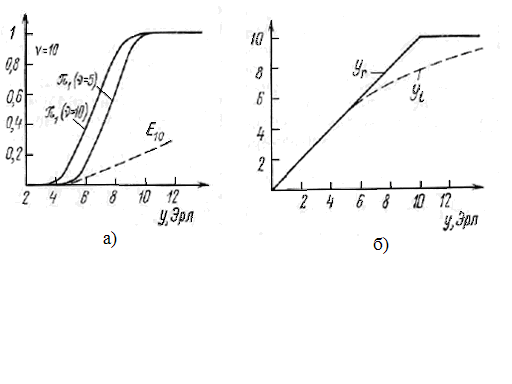
Рисунок 6.2. – Расхождения между традиционным подходом по теории Эрланга и по теории с учетом повторных попыток при наблюдениях: а) за потерянными попытками; б) за обслуженной нагрузкой

Воспользуемся снова рис. 6.2, чтобы подтвердить мысль, что до настоящего времени в нормировании качества телефонной связи недостаточно учитываются интересы абонента. Начнем с известной в математической статистике задачи «автобусы и пассажиры». Пассажиры жалуются, что автобусы переполнены. В то же время транспортное управление предлагает уменьшить число автобусных рейсов, так как, мол, автобусы ходят практически пустыми. И действительно, если в среднем на 10 автобусов в одном ехало 90 пассажиров, а в остальных девяти— по 10, то при опросе шоферов окажется, что в среднем автобус перевозит по 1/10(90+9∙10) = 18 пассажиров, а при опросе пассажиров совсем не так —в автобусе оказывается 1/180(90∙90+90∙10) =50 пассажиров.

Интересы телефонной администрации и абонентов также не совпадают. Положение абонентов характеризуют кривые на рис. 6.2: абоненты жалуются, что 50% вызовов теряется (рис. 6.2а), администрация же интересуется обслуженной нагрузкой (рис. 6.2б), которая определяет доходы телефонной станции. А тут все в порядке: кривая у_r незначительно превосходит запланированную нагрузку у_{i .}

О необходимости учитывать повторные попытки говорил еще Эрланг в начале 20 века. Однако только в последние годы разными авторами получены решения отдельных задач, связанных с повторными попытками, на основе которых можно создать инженерную методику расчета сетей связи с учетом повторных попыток. Это обстоятельство нашло отражение также в действиях МСЭ-Т; проблема повторных попыток признана важнейшей, обсуждаются различные теоретические подходы и статистические данные. Отметим две причины, объясняющие актуальность учета повторных попыток. Во-первых, необходимость учета дополнительной нагрузки, создаваемой повторными попытками. Особенно важно учесть их влияние на управляющие устройства, которые по мере централизации управления АТС становятся особенно дорогими; повторные попытки в основном влияют на управляющие устройства, так как каждая неудачная попытка ненадолго занимает соединительные линии, но создает полную нагрузку на управляющие устройства. Во-вторых, влияние повторных попыток на нагрузку сетей междугородной связи. Абонент, производящий междугородный вызов путем прямого набора номера, более резко переживает необходимость повторной попытки установить соединение, чем при местном вызове. Как показывают измерения, он более настойчиво добивается получения соединения, что, в свою очередь, при достаточно высокой нагрузке на сеть может привести к ее полной блокировке.

Еще актуальней проблема повторных попыток на международных сетях. На рис. 6.За представлен фрагмент международной автоматической сети связи, состоящий из 16 узлов и 15 пучков линий между ними [1].

Международный Консультативный Комитет по телефонии и телеграфии допускает вероятность блокировки 2% на звено сети (1% на узел и 1% на пучок линий) и 15—25% потерь при выходе к вызываемому абоненту. Если еще учесть вероятность ошибок набора, то даже при строгом соответствии реальных нагрузок расчетная вероятность безуспешной попытки будет не меньше 50%.

На рис. 6.3а показан сравнительно простой фрагмент сети, так как в нем не указаны обходные пучки, а дан только один путь – от абонента А к абоненту В. Однако принцип обходных путей (путей второго, третьего и т. д. выбора) повсеместно внедряется в автоматической сети связи. Поэтому при отсутствии свободных путей в каком-либо из 15 пучков или свободных устройств в каком-либо из 16 узлов сети, изображенной на рис. 6.3а, могут быть предусмотрены обходные пути (рис. 6.3б). Национальные сети будут иметь меньшее число звеньев, чем на рис. 6.3а, однако основные принципы сохраняются. В настоящее время происходит осмысливание влияния повторных попыток на сети связи, и, так как термины еще не установились, начнем с них.

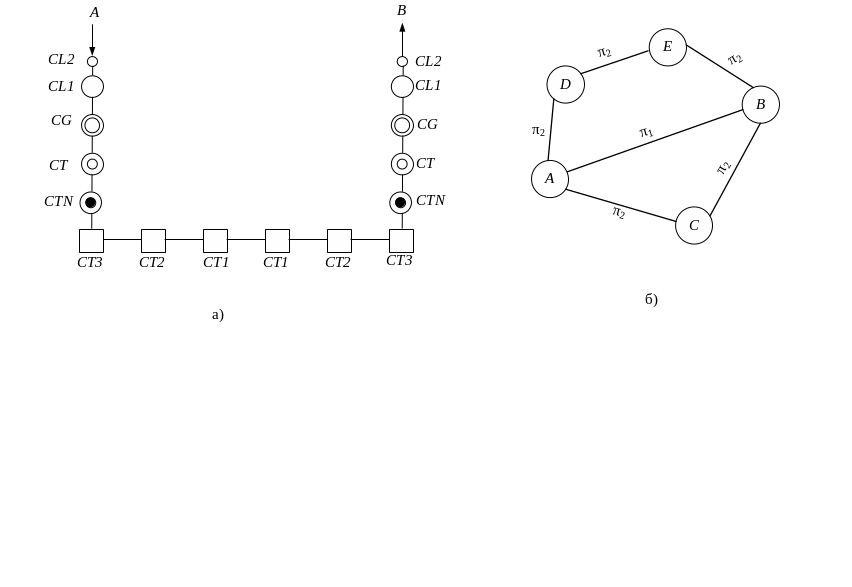
Рисунок 6.3 – Фрагменты сетей:

а) международная сеть; СТ 1, 2 и 3 — международные транзитные узлы 1; 2 и 3-й категорий, СТN — национальный транзитный узел, СG — узел зоны, СL 1,2 — местные узлы; б) иллюстрация обходных путей для сообщения между станциями A иB:путь первого выбора АВ, путь второго-выбора АСВ, путь третьего выбора ADEB, π₁ и π₂ — вероятности потери попытки на пучках.

Вызов — событие в сети связи, выражающееся в желании некоторого абонента (назовем его вызывающим) получить соединение с другим (вызываемым) абонентом, чтобы передать сообщение. Синоним вызова— требование. Вызов сопровождается попытками установить соединение. Последовательность попыток, порожденная одним вызовом, начинается с первичной попытки, после которой могут следовать повторные.

Попытки делятся на успешные (закончившиеся установлением соединения с вызываемым абонентом) и безуспешные. Вызовы делятся на обслуженные и потерянные. Для потерянного вызова последовательность порожденных им попыток кончается безуспешной попыткой. Можно говорить, что потерянный вызов сопровождается потерей передаваемого сообщения.

Повторяющий абонент – абонент, осуществляющий повторные по­пытки; он находится в очереди повторяющих абонентов.

Для определения качества сети связи используем следующие понятия:

вероятность потерн первичной попытки;

вероятность потерь общая или вероятность безуспешной попытки (отношение безуспешных попыток ко всем попыткам);

вероятность потери вызова (отношение потерянных вызовов ко всем вызовам);

среднее время доставки сообщения или среднее время пребывания в системе; оно исчисляется только для успешных вызовов и равно времени от момента поступления вызова (первичной попытки) до окончания разговора;

эффективная нагрузка (суммарное время занятости вызываемого абонента. Эффективная нагрузка совпадает с оплачиваемой нагрузкой);

общая нагрузка (суммарное время занятости вызывающего абонента);

доля эффективной нагрузки (отношение эффективной нагрузки к общей нагрузке) .