4. Порядок выполнения работы

1. Получить у преподавателя задание.

2. Решить задачи с использованием математического пакета, табличного процессора, системы программирования или вручную.

3. Показать решение преподавателю.

4. Составить отчет о лабораторной работе, включая постановку задачи, математическую модель, этапы решения и вывод. Отчет должен быть представлен к защите в письменном или электронном виде в конце семестра.

5. Отчет необходимо хранить до сдачи экзамена по данному курсу.

5. Литература

1. Фомин Я.А. Диагностика кризисного состояния предприятия. – М.: Юнити-Дана, 2003. - 349 с.

2. Горелик А.Л., Скрипкин В.А. Методы распознавания: Учебное пособие для вузов. Изд. 4-е, испр. – М: Высшая Школа, 2004г. – 261 с.

3. Ту Дж., Гонсалес Р. принципы распознавания образов. – М.: Мир, 1978. – 411 с.

4. Дуда Р., Харт П. Распознавание образов и анализ сцен. – М.: Мир, 1976. – 511 с.

5. Орехов Ю.В. Распознавание образов. Учебное пособие. УГАТУ. Уфа, 1995. – 45 с.

6. Горелик А.Л., Скрипкин В.А. Методы распознавания. – М.: Высшая школа, 1985. – 208 с.

Лабораторная работа №7. Байесовский классификатор в случае образов, характеризующихся нормальным распределением

1. Цель работы

Научиться составлять решающие функции с помощью байесовского классификатора в случае образов, характеризующихся нормальным распределением.

2. Теоретические сведения

Если известно или с достаточными основаниями можно считать, что плотности распределения функций правдоподобия р(х/ _i) суть многомерные нормальные (гауссовские), то применение синтезированного байесовского классификатора приводит к получению ряда интересных и хорошо известных решающих функций. Многомерная нормальная плотность распределения является объектом усиленного внимания в связи с удобством ее аналитической обработки. Кроме того, она представляет собой подходящую модель для множества важных прикладных задач. Для начала мы обратимся к одномерной плотности нормального распределения одной случайной переменной х:

,

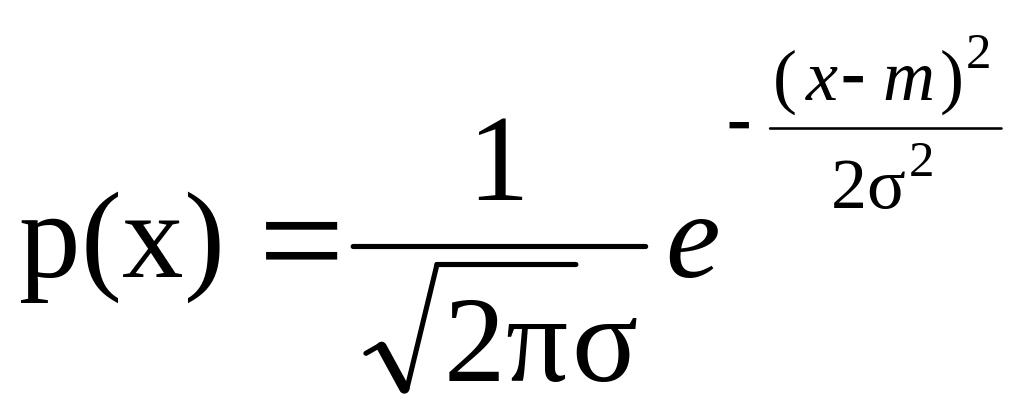
(1)

которая полностью определяется двумя параметрами – средним значением m и дисперсией ². Эти параметры в свою очередь определяются как

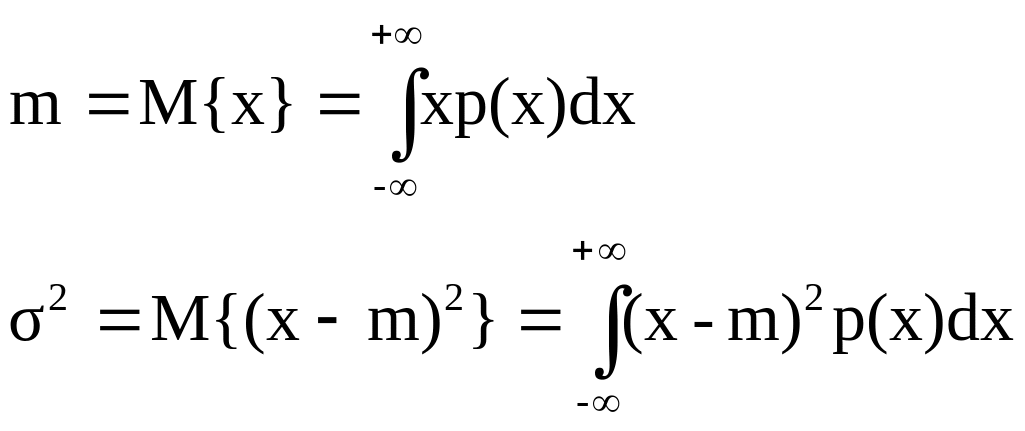
(2)

(3)

Так как плотность нормального распределения определяется двумя этими параметрами, то ее часто для простоты записывают как р(х)~N(m, ²). Образы, характеризующиеся нормальным распределением, проявляют тенденцию к группировке вокруг среднего значения, а их расстояние пропорционально среднеквадратичному отклонению . Около 95% объектов, извлеченных из совокупности с нормальным распределением, попадут в интервал, равный , и имеющий в качестве центра среднее значение.

Итак, рассмотрим М классов образов, описываемых многомерными плотностями нормального распределения

(4)

где каждая плотность распределения полностью определяется вектором средних значений m_i и ковариационной матрицей С_j, заданных соответственно как

(

5)

(6)

символ n обозначает в (4) размерность векторов образов, а запись |C_j| - определитель ковариационной матрицы C_j.

Ковариационная матрица C_j является симметрической и положительно полуопределенной. Ее диагональный элемент с_kk есть дисперсия k-го элемента вектора образов. Элемент c_ik, не стоящий на диагонали матрицы, представляет собой ковариацию случайных переменных х_i и х_k. Если переменные х_i и х_k статистически независимы, то элемент c_ik= 0. Многомерная плотность нормального распределения сводится к произведению одномерных плотностей нормальных распределений, если все недиагональные элементы ковариационной матрицы – нули.

Решающую функцию для класса ω_j можно выбрать в виде

.

В связи с тем, однако, что плотность нормального распределения выра­жается экспонентой, удобнее работать с натуральным логариф­мом от этой решающей функции. Другими словами, решающую функцию можно представить в виде

(7)

Подстановка выражения (4) в (7) приводит к

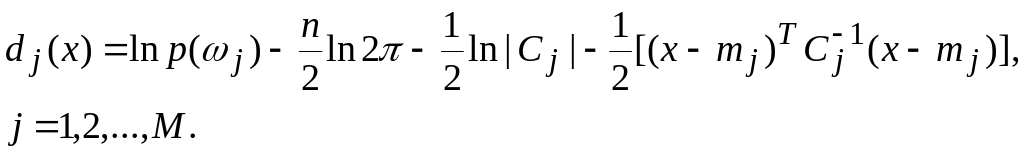(8)

Поскольку член (n/2)ln2π не зависит от j, его можно исклю­чить; при этом решающая функция d_j(x) примет вид

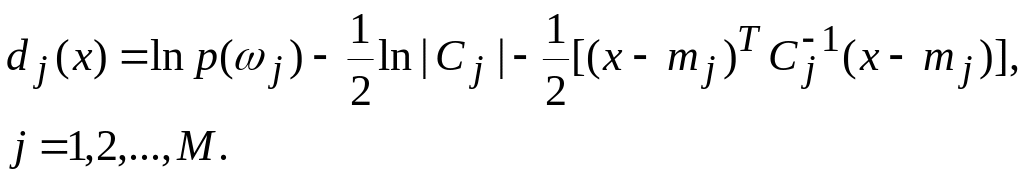(9)

Выражения (8) и (9) представляют байесовские ре­шающие функции для нормально распределенных образов.

Если для всех j=1,2,...,М ковариационные матрицы одинаковы, т. е. С_j= С, то легко можно показать, что удаление из соотношения (9) членов, не зависящих от значения, при­нимаемого индексом j, приводит к

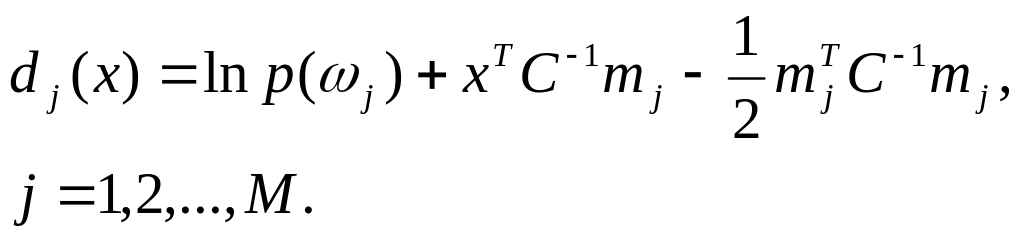(10)

это выражение представляет множество линейных решающих функций.

Если к тому же С= I, где I—единичная матрица, и вероят­ность появления класса ω_j, есть р(ω_j)== 1/M, j= 1, 2, ..., М, то выражение для решающей функции принимает вид

(11)

Из уравнения (10) следует, что paздeляющая гpaницa для классов ω_i, и ω_j, определяется как

(12)