Лабораторная работа № 6. Байесовская процедура распознавания, обеспечивающая минимальную вероятность ошибки классификации

1. Цель работы

Научиться составлять решающие функции с помощью байесовской процедуры распознавания, обеспечивающей минимальную вероятность ошибки классификации.

2. Теоретические сведения

Рассмотрим частный случай байесовской процедуры распознавания, когда потери от принятия любого неверного решения одинаковы (любое неверное решение одинаково нежелательно). В этом случае потери L(d_i=_i,_j) можно представить в виде

Условный риск получаем в виде

а это не что иное, как условная вероятность принятия решения при условии, что Х=х.

Величина R(d(x)=(x) / x) = 1 – P((x) / x) представляет собой условную вероятность принятия ошибочного решения при условии Х=х, если используется решающее правило d(x)= (x).

Байесовская процедура распознавания реализует такое правило d = , которое минимизирует R(d = ): в данном случае минимизирует вероятность принятия ошибочного решения – вероятность неправильной классификации объекта. Она дает

т.е. диктует выбор решения d_i = _i, если для всех j  i P(_i / x) > P(_j / x).

Полученную байесовскую процедуру можно записать в виде

т.е. в данном случае имеем набор решающих функций

Если априорный закон распределения неизвестен, то считают появление любого класса равновероятным, т.е. принимают

P(_j)=1/m, j=1,…,m

Согласно предположениям имеем

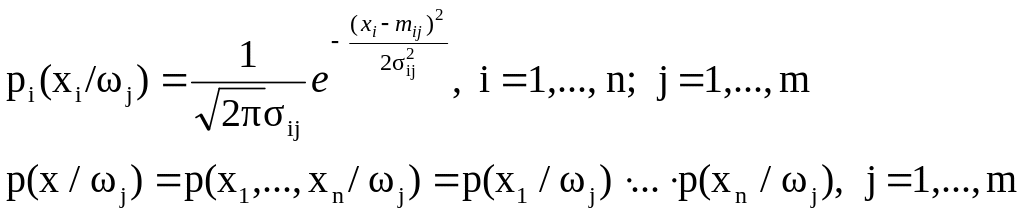
Байесовская процедура будет

Так так величины m_ij, _ij i=1,…,n, j=1,…,m неизвестны, вычислим их оценки по имеющимся представителям классов – обучающей выборке:

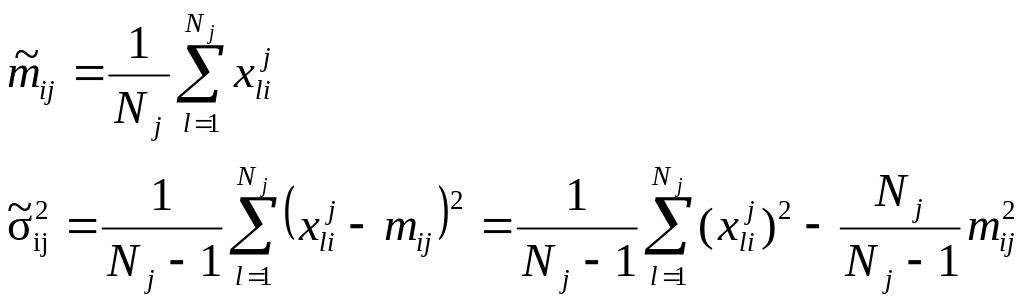
где N_j – число значений x_i^j , i=1,…,n в части обучающей выборки, отнесенной к классу _j i=1,…,m, x_li^j – l -ое значение x_i^j.

Можно показать, что используемые оценки состоятельные, несмещенные и эффективные.

3. Задание

Рассмотреть классы _j j=1,…,m . С помощью предложенной выше байесовской процедуры выяснить, к какому классу принадлежат образы х. Вывести значения оценок m_ij, _ij i=1,…,n, j=1,…,m , значения решающих функций P(х / _i) для исследуемых образов. Сделать вывод о принадлежности образа определенному классу.

1. ₁ = {(15; 0,80), (16; 0,70), (13; 0,85)}

₂ = {(25; 0,30), (26; 0,25), (27; 0,35), (0; 0,90)}

₃ = {(23; 0,95), (21; 0,90), (22; 0,98)}

x = (25; 0,80)

2. ₁ = {(15; 0,80), (16; 0,70), (13; 0,85)}

₂ = {(25; 0,30), (26; 0,25), (27; 0,35), (0; 0,90)}

₃ = {(23; 0,95), (21; 0,90), (22; 0,98)}

x = (15; 0,85)

3. ₁ = {(15; 0,80), (16; 0,70), (13; 0,85)}

₂ = {(25; 0,30), (26; 0,25), (27; 0,35), (0; 0,90)}

₃ = {(23; 0,95), (21; 0,90), (22; 0,98)}

x = (20; 0,65)

4. ₁ = {(15; 0,80), (16; 0,70), (13; 0,85)}

₂ = {(25; 0,30), (26; 0,25), (27; 0,35), (0; 0,90)}

₃ = {(23; 0,95), (21; 0,90), (22; 0,98)}

x = (22; 0,65)

5. ₁ = {(15; 0,80), (16; 0,70), (13; 0,85)}

₂ = {(25; 0,30), (26; 0,25), (27; 0,35), (0; 0,90)}

₃ = {(23; 0,95), (21; 0,90), (22; 0,98)}

x = (18; 0,55)

6. ₁ = {(15; 0,80), (16; 0,70), (13; 0,85)}

₂ = {(25; 0,30), (26; 0,25), (27; 0,35), (0; 0,90)}

₃ = {(23; 0,95), (21; 0,90), (22; 0,98)}

x = (14; 0,75)