- •Лабораторна робота №3
- •Задача 1.
- •1.Постановка задачі
- •2. Економіко-математична модель
- •5. Приклад розв’язку наведено нижче Рис. 3.2.
- •Лабораторна робота № 5
- •Лабораторна робота 6 Розв’язування задач нелінійного програмування в середовищі електронних таблиць Excel
- •Завдання 1
- •Завдання 2
- •Завдання 3
- •Завдання 4
- •Завдання 5
- •Лабораторна робота № 7
- •Лабораторна робота №8
- •Розв`язок
- •Аналіз розв’язку:
- •Лабораторна робота 8
- •Завдання в
- •Лабораторна робота №10
- •Завдання а.
ЛАБОРАТОРНА РОБОТА №1 Тема: Оптимальне використання ресурсів при плануванні робіт. Визначення оптимального ассортименту Мета роботи: навчитися працювати в діалоговому вікні пошук рішень Хід роботи 1. Постановка задачі Розрахувати максимальний прибуток цеху від продажу виробів А1, А2, А3. Ресурси - листи металу, пластмаса, деревина, гроші і прибуток від одного виробу.
2. Складання економіко-математичної моделі Економіко-математична модель задачі:
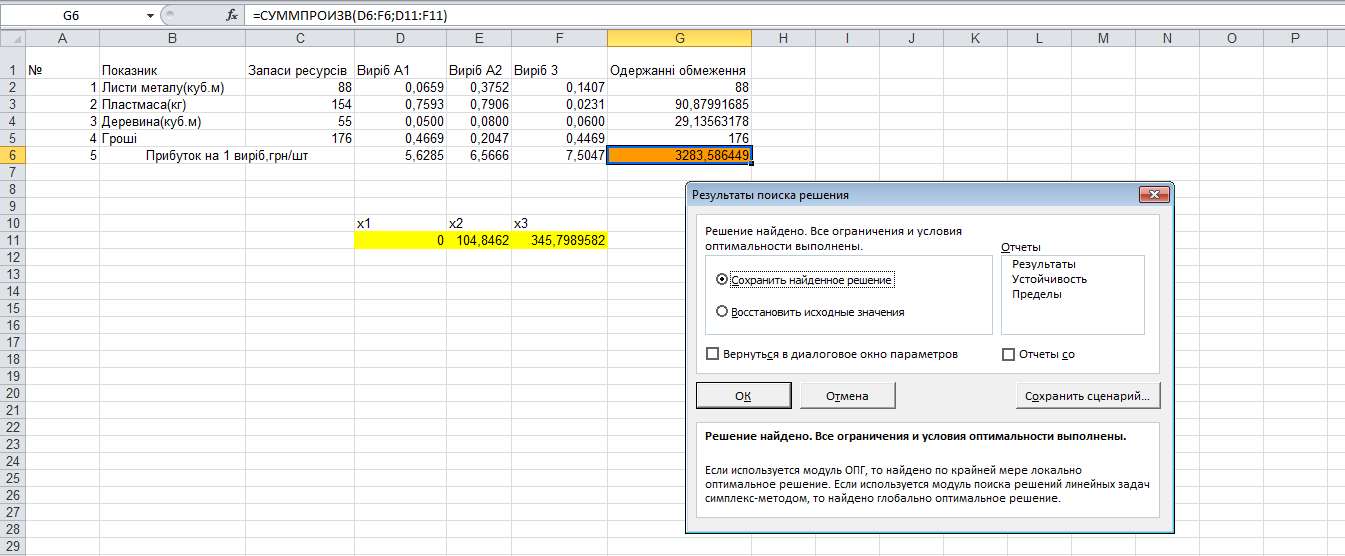
3. Вхідні дані В діапазон D4:F7 вводжу дані про витрати кожного виду ресурсу на одиницю відповідного виробу. В клітинки D8:F8 вводжу дані про ціну за одиницю відповідного виробу. В клітинках С4:С7 міститься інформація про задані обмеження. В клітинках G4: G7 обчислені одержані обмеження за допомогою функції „СУММПРОИЗВ”. І в клітинкахD11:F11 знаходиться вихідна інформація про необхідну кількість товару, що випускається для отримання найбільшого прибутку. В клітинці G8 записане значення отриманої цільової функції, значення якої обчислювалося за допомогою діалогового вікна „Пошук розв’язку”.
4. Приклад розв’язку задачі.
4. Висновок (аналіз даних) Виконуючи дану лабораторну роботу, я ознайомився із роботою діалогового вікна „Пошук розв’язку” та розв’язуванням задач за його допомогою. Згідно отриманого результату, бачимо, що максимальний прибуток цеху за даних обмежень можливий при випуску лише третього виробу. Прибуток при цьому становитиме 3283,58 грн.
|
ЛАБОРАТОРНА РОБОТА №2.
Тема:Розв’язування оптимізаційних задач лінійного програмування в середовищі електронних таблиць Excel
Хід роботи
ЗАВДАННЯ А.
Отримати рішення задачі лінійного програмування:
Завдання А.1
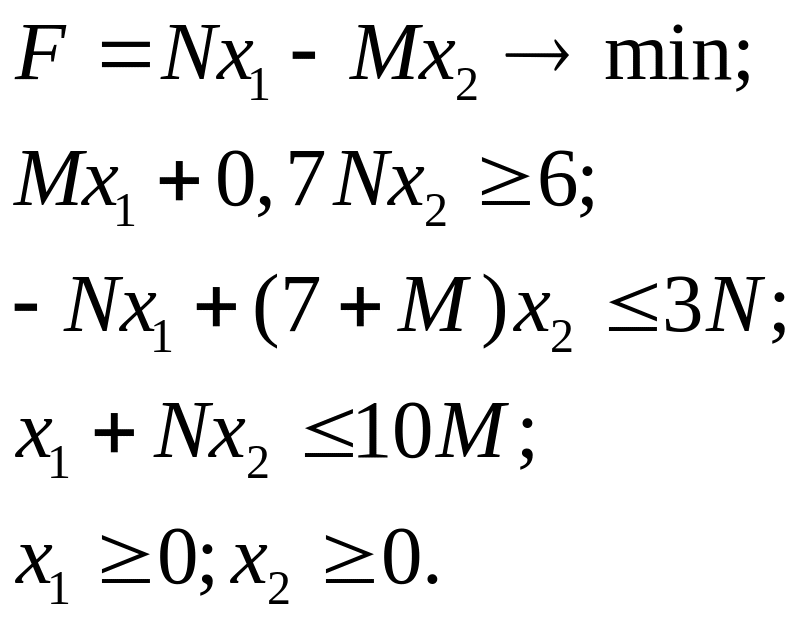
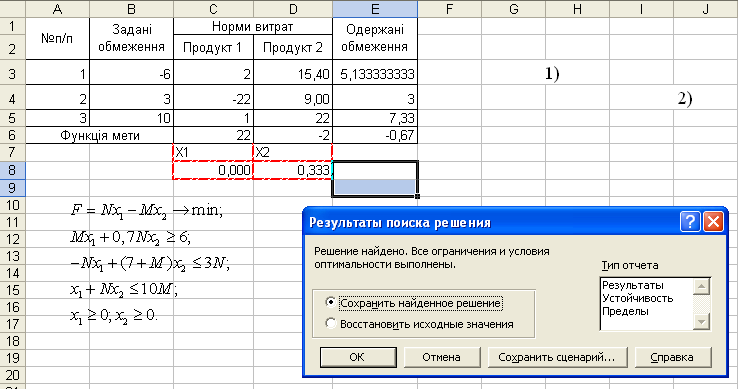
Завдання А.2

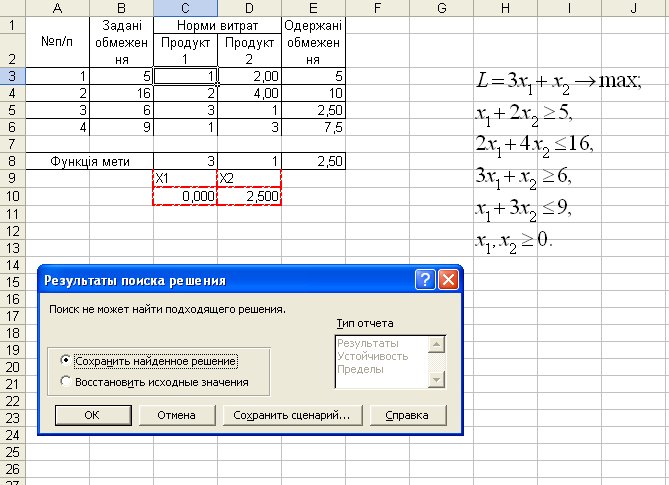
ЗАВДАННЯ В.
Отримати рішення задачі лінійного програмування:
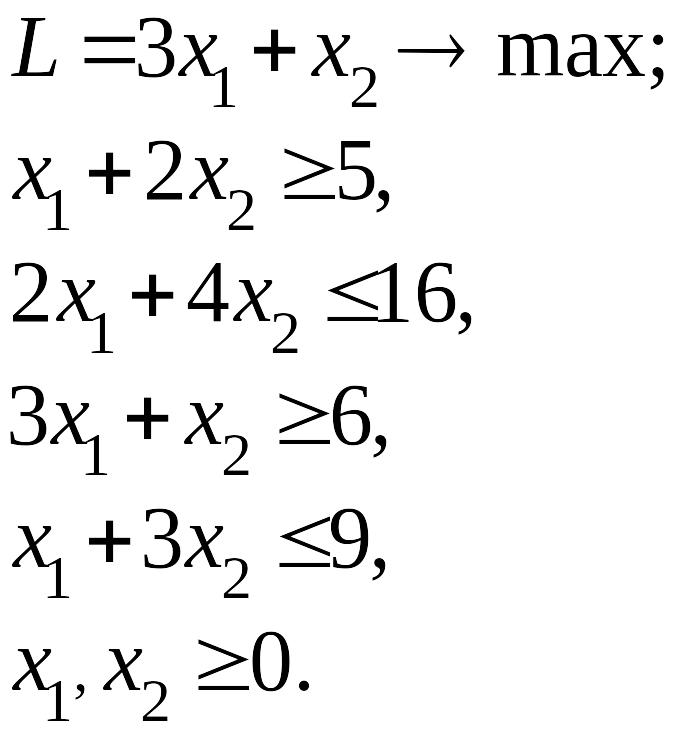
Тема: Транспортна
задача
Мета роботи:
навчитися розв’язувати транспортну
задачу за допомогою діалогового вікна
„Пошук розв’язку”.
ХІД РОБОТИЛабораторна робота №3
Задача 1.
1.Постановка задачі
Знайти оптимальний план перевезень деякого однорідного вантажу від постачальників П1, ..., П6 до користувачів К1, ..., К4. Критерієм оптимальності є мінімальна вартість доставки. Тарифи перевезень одиниці вантажу від і-го постачальника до j-го користувача, запаси вантажу в постачальників та потреби у вантажі користувачам
2. Економіко-математична модель
Математична модель транспортної задачі матиме такий вигляд:
F= (2+A)x11 + 3x12 + 8x13 + 7x14 + 4x21 + (6+A)x22 + 3x23 + 1x24 + 2x31 + 9x32 + (2+A)x33 + 3x34 + +4x41 + 5x42 + 4x43 + (4+A)x44 + 5x51 + 6x52 + 7x53 + 11x54 +1x61 + 10x62 + 2x63 + 7x64 min
![]() ,
,
де
N – порядковий номер курсанта в списку
журналу, А=![]()
хij – кількість одиниць товару, що планується перевезти з і-го в j-й пункт
В діапазон комірок В15:АЕ25 вводжу розподіл кожного постачальника на кожного користувача (1-й постачальник поставляє товар 5 користувачам і т. д.). АF15:АF25 вводжу задані обмеження (права частина системи обмежень). Діапазон АG15:АG25 одержані обмеження за допомогою функції СУММПРОИЗВ. В26:АЕ26 – вартість транспортування від і-го постачальника до J – го користувача. В комірці АF26 записане значення функції мети. В30:АЕ30 – кількість одиниць товару, що перевозиться і-м постачальником J-му користувачеві (Див. рис. 3.1.)
4. Висновок (аналіз розв’язку задачі)
Користуючись для знаходження розв’язку транспортної задачі діалоговим вікном „Пошук розв’язку” я отримав результати, зображені на мал. 1. Для розв’язку задачі я ввів фіктивного користувача К5 для закриття задачі. Я отримав такі результати: 1-й постачальник перевозить 1-му користувачеві 220 одиниць товару, 2-му – 330, 5-му – 110, 2-й постачальник транспортує 4-му користувачеві 110 одиниць товару, 3- постачальник перевозить 4-му користувачеві 330 одиниць, 4-й постачальник 4-му користувачеві – 440 одиниць товару, 5-й постачальник 5-му коритсувачеві – 440 одиниць та 6-й постачальник надає 3-му користувачеві 110 одиниць товару. За такого розподілу забезпечується мінімальна вартість доставки і становить 1320 грошових одиниць.
Задача
2:
У транспортному
вузлі є причали А1, А2, А3, А4, А5 для
перевалки піску відповідно 10, 40, 80, 90,
10 тис. т. Пісок доставляється автотранспортом
до 7 районів міста П1-П7, їх потреба у
піску становить відповідно 20, 30, 55, 25,
80, 100, 10 тис. т. Вартість завантаження
піску в автомобіль на всіх причалах
однакова. Питому відстань перевезення
lij (км) від i-го причалу до j-го
району наведено в таблиці. Визначити
оптимальний план обслуговування
причалів і споживачів автотранспортом,
за якого буде виконано план перевезення
і пробіг автомобілів буде мінімальним.
Система обмежень:
F
де хij –
кількість одиниць товару, що планується
перевезти з і-го в j-й пункт
3. Вхідні дані
В діапазон комірок
В4:АQ16 вводжу розподіл кожного постачальника
на кожного користувача (1-й постачальник
поставляє товар 5 користувачам і т. д.).
АR4:АR16 вводжу задані обмеження (права
частина системи обмежень). Діапазон
АS4:АS16 одержані обмеження за допомогою
функції СУММПРОИЗВ. В17:АQ17 – вартість
транспортування від і-го постачальника
до J – го
користувача. В комірці АR17 записане
значення функції мети. В21:АQ21 – кількість
одиниць товару, що перевозиться і-м
постачальником J-му
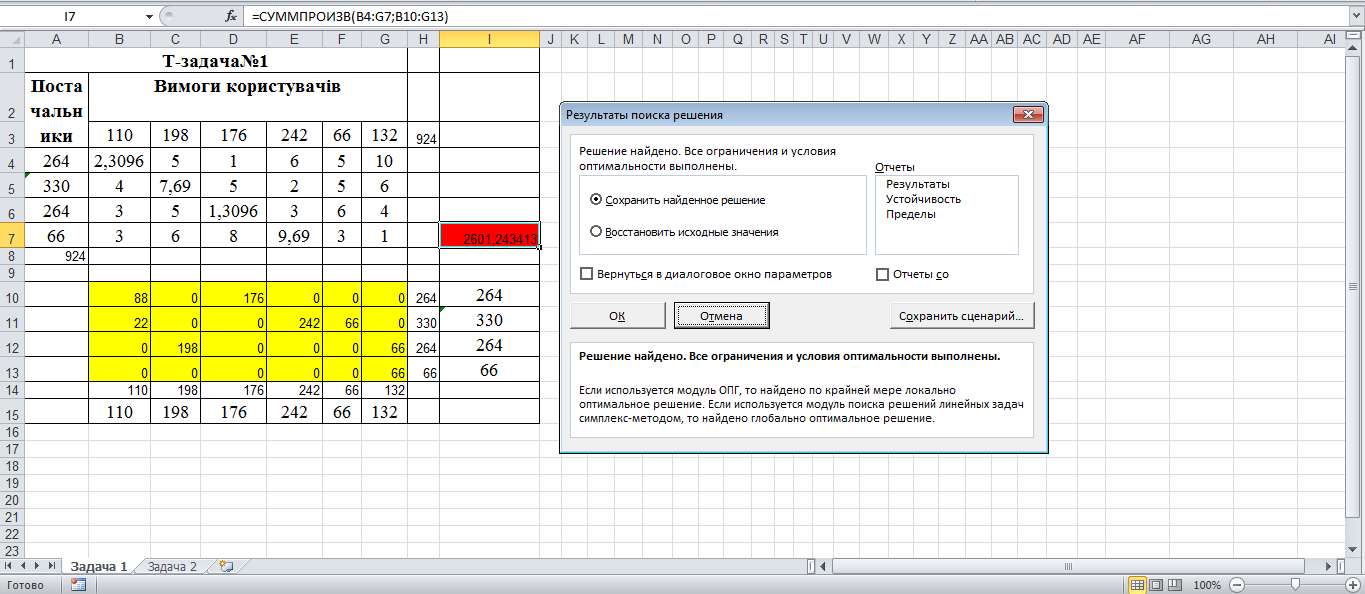
користувачеві (Рис. 3.2.)
1.Постановка задачі
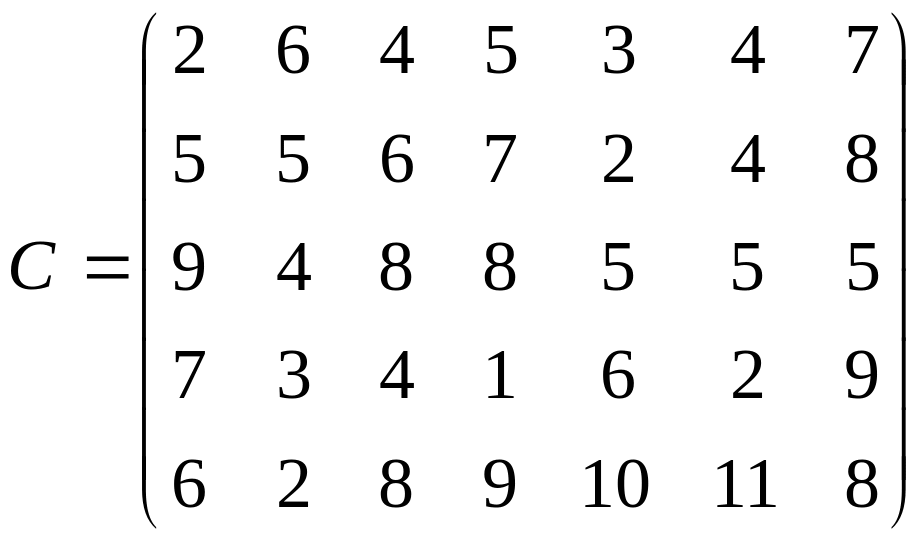
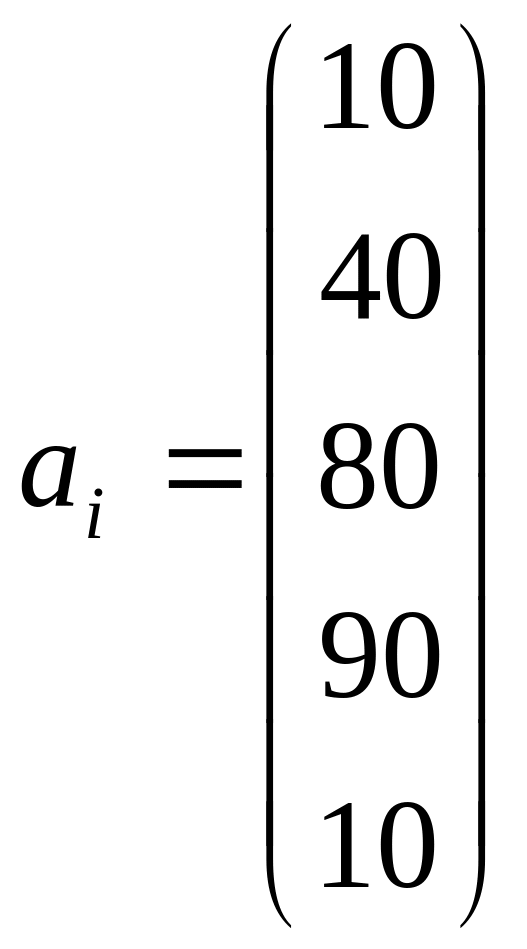
![]()
2. Економіко-математична модель
 =
2x11 + 6x12 + 4x13 + 5x14 +
3х15 + 4х16 + 7х17 + 5x21 +
5x22 + 6x23 + 7x24 + 2х25
+ 4х26 + 8х27 + +9x31 +
4x32 + 8x33 + 8x34 + 5х35
+ 5х36 + 5х37 + 7x41 + 3x42
+ 4x43 + 1x44 + 6х15 + 2х16
+ 9х17 + 6x51 + 2x52 + +8x53
+ 9x54 + 10х55 + 11х56 +
8х57 min
=
2x11 + 6x12 + 4x13 + 5x14 +
3х15 + 4х16 + 7х17 + 5x21 +
5x22 + 6x23 + 7x24 + 2х25
+ 4х26 + 8х27 + +9x31 +
4x32 + 8x33 + 8x34 + 5х35
+ 5х36 + 5х37 + 7x41 + 3x42
+ 4x43 + 1x44 + 6х15 + 2х16
+ 9х17 + 6x51 + 2x52 + +8x53
+ 9x54 + 10х55 + 11х56 +
8х57 min![]()
Користуючись для знаходження розв’язку транспортної задачі діалоговим вікном „Пошук розв’язку” я отримав результати, зображені на мал. 3.2. Для розв’язку задачі я ввів фіктивного постачальника А6 для закриття задачі. Я отримав такі результати: з 1-го причалу доставляють в 1-й район 10 тис. т, з 2-го причалу привозять в 5-й район 40 тис. т, з 3-го причалу в 2-й район – 20, в 5-й район – 40 тис. т, в 6-й район – 20 тис. т, з 4-го прчалу доставляють в 4-й та 6-й райони міста відповідно 25 та 65 тис. т піску, з 5-го причалу транспортують в 2-й район міста 10 тис. т піску. За такого розподілу забезпечується мінімальна пробіг автомобілів, який становить 655км.

 5,63х1+6,56х2+7,50х3
Fmax
5,63х1+6,56х2+7,50х3
Fmax