4. Фігури нульової площі.

З означення квадровних фігур випливає, що якщо зовнішня площа фігури Ф дорівнює нулю: , то сама фігура є квадровною (бо ) і

Теорема 1.6. (напівадитивність верхньої міри). Для довільних фігур Ф₁, Ф₂, … ,Ф_m площини має місце нерівність:

(1.16)

де .

Доведення. Оскільки кожний квадрат -го рангу, який має принаймні одну спільну точку з , має принаймні одну спільну точку з деякою множиною , то

.

В останній нерівності перейдемо до границі при :

■

З теореми, зокрема, випливає, що об’єднання довільної скінченної множини квадровних фігур нульової площі є фігура нульової площі.

Приклад 6. Множина точок справнювальної дуги Жордана є фігура нульової площі.

Теорема 1.7. Для того, щоб фігура була квадровною, необхідно і достатньо, щоб межа була квадровною і мала площу 0.

Теорема 1.8. Для того щоб обмежена множина була квадровною, необхідно і досить, щоб для довільного ε>0 існувала скінченна система прямокутників попарно без спільних внутрішніх точок, і така: 1) яка б покривала усі межові точки множини і 2) сума площ прямокутників цієї системи була б меншою від .

Доведення прикладу 6 і теорем 1.7-1.8 можна знайти в підручниках [Кудр., ст. 293-], [Давидов, ст.106], [Райков, Многом., ст. 153-154], [Никольський С.М. Курс м/а.: В 2-х т. –М.: Наука, 1973.-Т. 2]

Т еорема 1.9. Об’єднання, перетин і різниця двох квадровних фігур є фігура квадровна.

Доведення. Якщо , , або то (рис. 1.21) Оскільки фігури і квадровні, то , також .

Тому і за теоремою 1.7 фігура квадровна. ■

Зауваження. Теорему 1.9 можна поширити на об’єднання і перетин довільної скінченної множини квадровних фігур, при чому .

Теорема 1.10 (адитивність міри). Площа фігури, яка є об’єднаннями скінченного числа квадровних фігур , які попарно не перетинаються, дорівнює сумі площ цих фігур:

.

Доведення. Оскільки для довільного n правильне включення , , то і , , тому згідно з (1.2)

. (1.7)

Якщо квадрат рангу належить множині , то він належить і об’єднанню 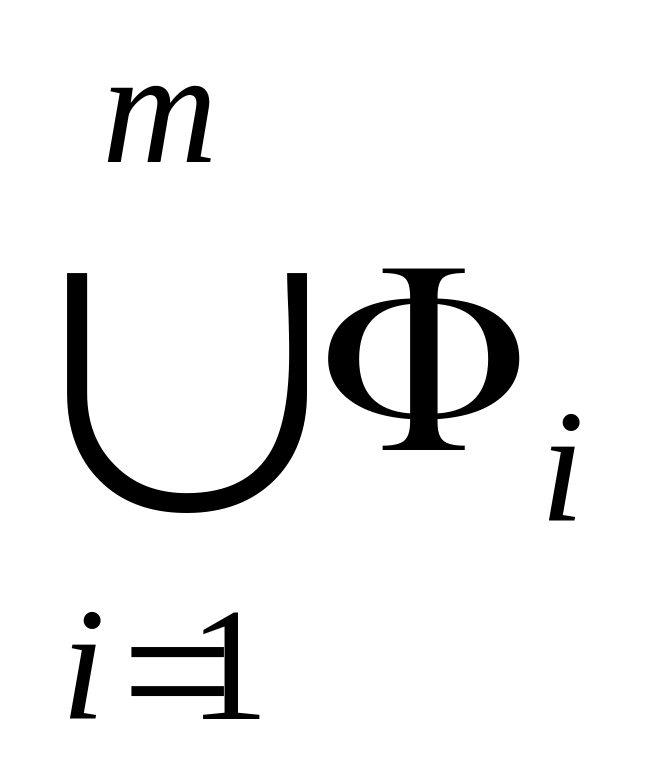цих множин, отже

,

Звідки в силу монотонності міри і рівності (1.17), випливає:

.

Перейдемо до границі при :

. (1.18)

З іншого боку, для довільних відмінних множин має місце нерівність (1.16) ( )

(1.19)

З нерівностей (1.18) і (1.19) і випливає потрібна рівність. ■

5. Кубовні тіла.

Написати твір на тему «Кубовні тіла».

Програма дій.

1. Дайте означення внутрішнього і зовнішнього об’єму тіла кубовного тіла.

Простір площинами , , ( ) для кожного цілого розбивається на рівні куби рангу n:

.

Тілом називають довільну обмежену множину точок простору .

Для тіла ввести позначення , , , :

, ,

і довести твердження:

1) ( ) – зростаюча послідовність невід’ємних чисел,

( ) – спадна, при чому ;

2) , яку існують внутрішнім об’ємом тіла ;

3) , яку називають зовнішнім об’ємом тіла E;

4) .

Якщо , то множину називають кубовним тілом, а число - об’ємом цього тіла.

2. Основні властивості кубовних тіл.

Теорія кубовних тіл будується аналогічно теорії квадровних фігур. Зокрема треба довести наступні твердження.

1. Монотонність і адетивність об’єму;

2. Кубовність прямокутного паралелепіпеда і .

3. Тіло кубовне тоді і тільки тоді, коли 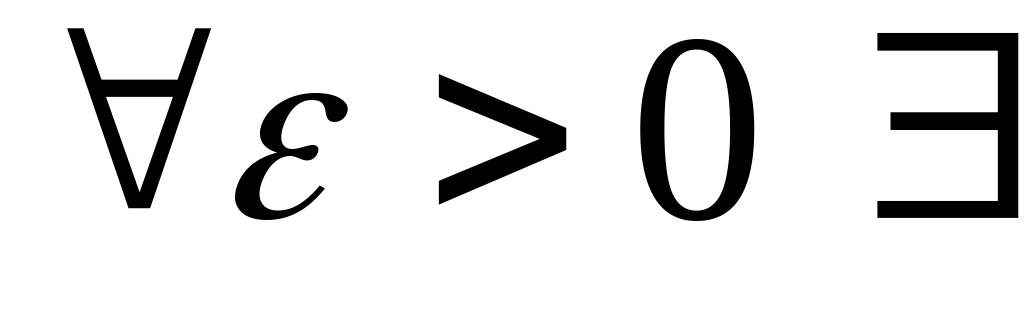кубовні тіла і такі, що і .

4. Тіло кубовне тоді і тільки тоді, коли його межа кубвна і має нульовий об’єм.

5. Всяка плоска фігура в просторі кубовна і має нульовий об’єм.

6. Зв’язок між площами і об’ємами.

Нехай – довільна фігура в площині і - довільний відрізок на осі .

Означення. Циліндричним тілом називають множину точок простору (рис. 1.22)

.

Т еорема. Якщо Фігура квадровна, то циліндричне тіло кубовне і .

Доведення. Похначемо через і квадрати рангу , які які відповідно містяться і мають принаймні одну спільну точку з , я через і циліндричні тіла, які складаються із скінченного числа прямокутних паралелепіпедів таких, що

.

Ці тіла є кубовними,а їх об’єми

,

.

Оскільки фігура квадровна, то і

Для деякого . Отже, тіло кубовне і , звідки і випливає потрібна рівність. ■

3. Рисунки до побудованої теорії виконайте в графічному редакторі.

16