Лекція 1

Тема 11.75. Квадровні фігури і кубовні тіла

План

1. Поняття внутрішньої, зовнішньої площі плоскої фігури, квадровної фігури.

2. Властивості площі квадровної плоскої фігури.

3. Приклади квадровних фігур.

4. Фігури нульової площі.

5. Кубовні тіла.

1. Поняття внутрішньої, зовнішньої площі плоскої фігури, квадровної фігури

Поняття площі плоскої фігури було введено нами в темі 6.39 «Застосування визначених інтегралів» [ст. 91]. В цій лекції визначимо клас квадровних фігур, який включає у себе всі плоскі фігури, відомі в шкільному курсі математики, а також вивчимо властивості квадровних фігур (зокрема монотонність і адитивність).

Означення 1.1. Плоскою фігурою називають довільну обмежену множину точок довільного простору (площина).

На площині прямі , , 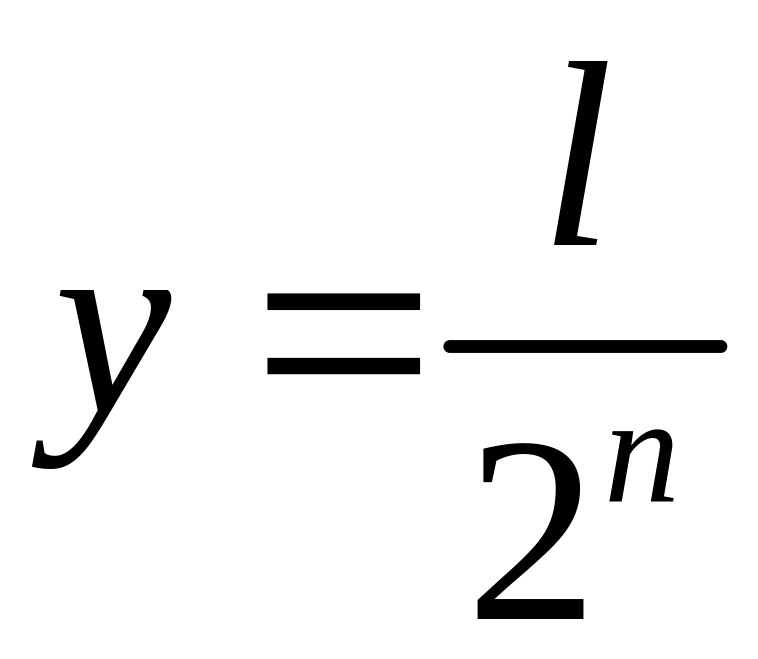розбивають площину на два рівні квадрати , які називають квадратами рангу і позначають .

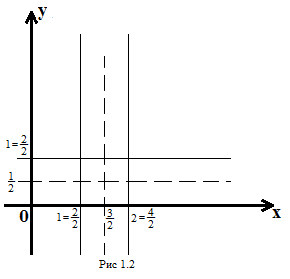
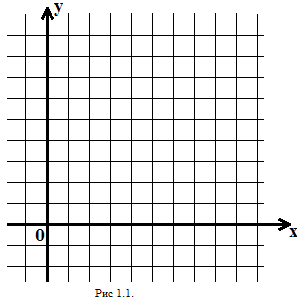
П ри переході від до кожний квадрат рангу розбивається на чотири квадрати рангу (рис. 1.1).

Множина всіх квадратів рангу очевидно покриває усю множину (рис. 1.2). Два квадрати одного рангу можуть мати спільними лише деякі свої межові точки.

Означення 1.2. Площею квадрата рангу називають число

.

Якщо множина є об’єднанням скінченного числа або зчисленної множини квадратів даного рангу n

,

то її площа дорівнює:

.

Зрозуміло, що або .

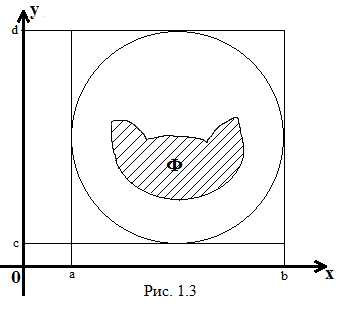
Нехай тепер – довільна плоска фігура тобто вона міститься у відкритому крузі, який, в свою чергу, міститься у деякому прямокутнику ( – проекція круга на вісь абсцис, – на вісь ординат) (рис. 1.3)

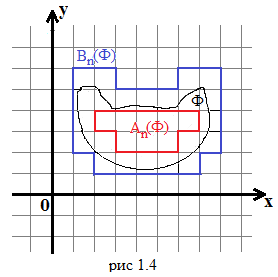
Отже, може бути лише скінченна або порожня множина квадратів рангу , яка міститься всередині фігури , і також лише скінченна (1.1) або порожня множина квадратів рангу , кожний з яких має принаймні одну спільну точку з . Позначимо:

, , (1.1)

, , (1.2)

де – число квадратів рангу , які містяться всередині , а – які перетинаються з (рис 1.4). При цьому множина строго лежить всередині , тобто не перетинається з його межею.

Властивості чисел .

Властивість 1.1. Для довільного цілого :

, і

при

Д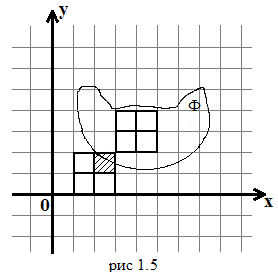 оведення. Дійсно, якщо квадрат рангу міститься всередині , то і всі чотири квадрати рангу , з яких він складається, також міститься всередині , тому .

З другого боку число квадратів рангу , з яких складається квадрат рангу , і які перетинаються з , дорівнює , і серед них міститься кожний квадрат рангу , що перетинається з ; отже (рис 1.5).

Тому

i ■

Властивість 1.2. Для довільних цілих :

.

Доведення. Розглянемо випадки

1. , оскільки кожний квадрат, який міститься всередині , перетинається з ;

б) якщо на основі властивості 1.1, а , отже ;

в) якщо , то на основі властивості 1.1, і а , (умова а)) отже ;

отже ми отримали дві монотонні послідовності невід’ємних чисел:

,

,

які є обмеженими відповідно зверху, знизу. Тому і відповідно точна верхня і точна нижня межі цих послідовностей:

, .

Означення 1.2. Точну верхню межу послідовності називають внутрішньою площею фігури і позначають :

, (1.3)

а точну нижню межу послідовності – зовнішньою площею фігури і позначають:

. (1.4)

Очевидно, що . На основі відомої теореми про границю монотонної послідовності маємо:

(1.5)

Зауваження. Існують плоскі фігури, для яких . Наприклад якщо розглянути множину точок квадрата з раціональними координатами, то

і , а і

Отже .

Означення 1.3. Якщо внутрішня і зовнішня площі плоскої фігури співпадають, то називають квадровною фігурою, а спільне значення називають площею фігури:

(1.6)

Таким чином (1.7)

або (1.8)