Замечание.

Величинадвойногоинтеграланедолжназависетьотпосле-довательностипеременныхинтегрированиявповторноминте-грале.Однаковслучаеб)можноотметить,чтововнешнемин-тегралепервообразнаянаходитсязначительнобыстрее,безпривлеченияметодазаменыпеременнойвопределенноминте-грале.

Задача2.Вычислитьдвойнойинтеграл_∫∫(x−y)dxdy,если

D

областьDограниченапрямыми

yx,y2x,

x2,

x3.

Решение:

ОбластьинтегрированияDдвойногоинтегралаобладаетнекоторойособен-

ностью(рис.7).Лучи,пересекающиеобластьDпараллельнооси0yи0x,неявляютсяэквивалентными.Всамомде-ле,точкивходалучавпервомслучае

расположенынапрямой

yx,

авыхо-

Рис.7.

да—

y2x.Авовторомслучае(лучи

параллельны0x)точкивходавDраспо-

ложенынадвухпрямых,

x2,и

x^1y.Точкивыходалуча

2

такжерасположенынадвухпрямых,

x3,и

xy.Длязапи-

сиповторныхинтеграловнеобходимо,чтобыточкивходаивы-ходабылирасположенынаобщейпрямой.Этомуусловиюудо-влетворяетслучайзаписивнутреннегоинтегралапоперемен-нойy.Есливыбираетсяинтегралпопеременнойx,тогдаоб-

ластьDдолжнабытьразделенана3области(рис.7,областиотмеченыкака,б,в),вкоторыхточкивходапринадлежатод-нойпрямой,точкивыходатакжепринадлежатоднойпрямой.Вычислениедвойногоинтегралавэтомслучаесущественноусложнится.Такимобразом,длявычислениядвойногоинте-гралавнутреннийинтегралопределимпоy.

3 2x

32x 2x

_∫∫(x−y)dxdy_∫dx_∫(x−y)dy_∫[_∫xdy−

_∫ydy]dx

D 2 x

2x x

3

_∫[xy|^2x

_y² 3

− |^2x]dx_∫[x(2x−x)−

(4x²⁻x²⁾

]dx

2 ^{x 2x} 2 ²

₃ 2 3 3 3

_∫[x^2−(3x

⁾]dx^x

_|3−3x

|^3−^x

_{|3−}27−8_−19_.

2 ^{2 32 6 2 62 6 6}

Задача3.Изменитьпорядокинтегрированиявдвойномин-

теграле

1

_∫dy

0

3−y²

_∫f(x,y)dx.

_y2

2

Решение:

Вповторноминтеграленеобходимоперейтикдругойпо-следовательностипеременныхинтегрирования.Внутренний

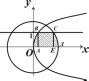интеграл—попеременнойx,внешний—y.Поуказаннымпреде-ламвосстановимобластьинтегри-рованияD,котораяограничивается

двумяпрямыми:

2

y0,

y1,пара-

болой

x^y,

2

ветви которой

направленывдольоси0x,атакже

Рис.8.

окружностьюx

3−y^2.

Окруж-

ностьприведемкканоническомувиду

x^2y^23.

Следова-

тельно,еерадиусравен 3,ацентрнаходитсявточке

O(0,0),

(рис.8).Областьинтегрированияуказанаштриховкой.Найдемпределыинтегрированиядлявнутреннегоинтегралапопере-меннойy.ОбластьинтегрированиядолжнабытьразделенанаобластиOВA,ABCE,ECД.Всамомделе,точкивходалучей,пересекающихобластьD,(проводятсяпараллельно0y)распо-ложенынаоси0x,ноточкивыходарасположенынатрехраз-

ныхлиниях.ВобластиOВAнапараболеOВ(т.е.y

2x),в

областиABCEнапрямойBC(т.е.

y1),вобластиECДна

окружностиCД(т.е.y

2. −x^2).Найдемпределыинтегриро-

ваниявнешнегоинтегралавуказанныхобластях.Вобласти

OВA

x∈[0,^1],

2

вобластиABCE

x∈[^1,

2

2],

вобластиECД

x∈[2,

3].

Указанныепределыинтегрированиянаходятся

решением системы уравнений

^ y

2

_x ,

_ 2



y1_, а также



^x

3−y^2,

y1^.Такимобразом,повторныйинтегралза-

пишетсявследующемвиде:

₁ 3−y²

_∫dy_∫

_{0 y2}

2

1

f(x,y)dx

_∫f(x,y)ds

OBA

_∫f(x,y)ds

ABCE

_∫f(x,y)ds

ECD

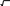
2 ^{2x 2 1}

3 3−x²

_∫dx

_∫f(x,y)dy_∫dx_∫f(x,y)dy_∫dx

_∫f(x,y)dy.

^{0 0 1 0} 2 ⁰

2

Задача4.Вычислитьплощадьфигуры,ограниченнойлини-ей(2y^22x^2)28x^3.

Уравнениелинии,записанноевдекартовойсистемекоор-динат,существенноупроститсяприпереходекполярнойси-

стеме.Формулыпереходаследующие

xρcosϕ,

yρsinϕ,

гдеϕ,

ρ–координатыточеквполярнойсистемекоординат.

Подставимвуравнение

(2ρ²sin²⁽ϕ)2ρ²cos²⁽ϕ))^28ρ³cos³⁽ϕ).

4ρ^4(sin2(ϕ)cos²⁽ϕ))^28ρ³cos³⁽ϕ)⇒ρ2cos³⁽ϕ).

Построимграфикфункции

ρ2cos³⁽ϕ)

вполярнойсисте-

мекоординат(рис.9).Дляэтоговыбираемзначениеугла,рав-

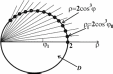ногоϕ=ϕ₁,вычисляемрадиусρ₁,которыйоткладываемналуче,наклоненномподугломϕ=ϕ_1кполярнойосиит.д.Нарис.9приведенграфикфункцииρ2cos³⁽ϕ).Фигураявляется

симметричной.Всоответствиисосвойствамидвойныхинтегра-

Рис.9.

ловплощадьобластиинтегриро-ванияDсовпадаетсдвойным

интегралом.Поформуле(4)тогда(подинтегральнаяфункцияравнаединице)площадьбудетравна

β

S_D_∫∫dxdy_∫dϕ

ρ₂₍ϕ)

_∫ρdρ.

D α ρ₁₍ϕ)

Взадании(рис.9)уголϕиρизменяютсявинтервале

ϕ∈[−^π,π],

ρ∈[0,2cos^3ϕ]соответственно.Следовательно,

22

π π π π

₂ 2cos³ϕ

_{2 ρ}2

^{3 24}cos^{6ϕ 2}

S_D2_∫dϕ

_∫ρdρ2_∫dϕ

_|2cosϕ_2∫[

]dϕ4_∫cos^6ϕdϕ

0

0 0 0 ² 0 ² 0

Длянахожденияпервообразнойнеобходимопонизитьпо-рядокстепенивподинтегральнойфункции.

π

2

4_∫(

0

1cos(2ϕ)

2

)^3dϕ

π

1. 2

_∫(13cos(2ϕ)3cos²⁽2ϕ)cos³⁽2ϕ))dϕ

2. 0

π

1. 2

 _∫dϕ

2. 0

π

3. 2

_∫cos(2ϕ)dϕ

2. 0

π

2. 2

_∫cos²⁽2ϕ)dϕ

²⁰

π

π

1. 2

_∫cos³⁽2ϕ)dϕ

2. 0

π

₁ π

0

 ϕ|²

2

3. π

0

 sin(2ϕ)|²

4

₃₂

 _∫[1cos(4ϕ)]dϕ

²⁰

1. 2

_∫cos³⁽2ϕ)dϕ

2. 0

^π0

4

π

3. 2

_∫dϕ

2. 0

π

2. 2

_∫cos(4ϕ)dϕ

²⁰

π

π

1. 2

_∫cos³⁽2ϕ)dϕ

2. 0

^π

4

3π_3

4 8

π

π

0

sin(4ϕ)|²

1. 2

 _∫cos²⁽2ϕ)d(sin(2ϕ))

2. 0

π

π0

1. 2

_∫(1−sin²⁽2ϕ))d(sin(2ϕ))π

2. 0

1. 2

_∫d(sin(2ϕ))−

2. 0

0

π

−^1[sin(2ϕ)]^3|2π

3

₁ π

0

sin(2ϕ)|²

2

−¹⁰π.

3

Прирешениизадачдляпониженияпорядкабылаиспользо-

ванатригонометрическаяформулатакже(ab)^3a^33ab^23a^2bb^2.

1cos(2ϕ)2cos²⁽ϕ),а

Задача5.Вычислитьа).Тройнойинтеграл_∫∫∫x^2yzdxdydz,

V

если область интегрирования V ограничена плоскостями

x0,

y0,

z0

xyz2.

б).Вычислитьобъемпро-

странственноготела,ограниченногоуказаннымиплоскостями.

а).Областьинтегрированияограниченаплоскостями.Нарис.10приведенапространственнаяфигура.Проекциейпро-странственноготеласлужиттреугольник,образованныйпря-

мыми

x0,

y0,

xy2.Следовательно,

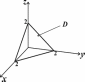2

_∫∫∫x^2yzdxdydz_∫x^2dx

2−x

∫

ydy

2−x−y

_∫zdz

V 0 0 0

2

_∫x^2dx

0

2−x

∫

0

(2−x−y)²

y

2

dy

1. 2

 _∫x

2. 0

0

₁₂

^2dx

2−x

_∫y[(2−x)²

0

_y2

−2y(2−x)y²

|



_y3

]dy

^Рис.10. 

_∫x^2[(2−x)² |^2−x

−2(2−x)

2−x

0

0

4

^y|2−x]dx

4

1. 2

_∫x^2[

2. 0

²⁰

(2−x)⁴

2

2

(2−x)⁴

• 2

3

(2−x)⁴



4

3

)dx

₁₂

 _∫x²⁽2−x)⁴⁾dx

16_.

²⁴⁰

315

б).Объемпространственноготела(рис.10)всоответствиисформулой(14)равен

2

V_∫∫∫dxdydz_∫dx

2−x

∫

2−x−y

dy_∫

2

dz_∫dx

2−x

0

_∫[z|^{2−x−y]}dy

2

V 0 0 0 0 0

2

_∫dx

2−x 2

0

_∫[2−x−y]dy_∫[2y|^2−x

• xy

2−x

|

0

• ^y|2−x]dx

0 0 0

0

² (2−x)²

2

_{2 x2}

_∫[2(2−x)−x(2−x)−

0 ²

3

2x|²⁻x^2|2^x

]dx_∫[2−2x

0

|^24−4^8^4.

]]dx

2

0 0 _{60 6 3}

Задача6.Вычислитькриволинейныйинтеграл_∫(x−y)ds,

L

гдеLотрезокпрямойотA(0,0)доB(4,3).