Определение.

Если существует конечныйпределинтегральныхсуммпри

λmax∆d_i

→0,причемэтотпределнезависитотспособа

разбиенияобластиVнаnобъемов,атакжепроизвольноговы-

n−1

бораточекP(х_i,у_i,zi),тогдаσlim_∑f(x_i

λ→0_i0

,y_i

,z_i

)∆v_i

называет-

сятройныминтеграломотфункцииf(х,у,z)пообластиVиобозначаетсясимволом

def

n−1

_∫∫∫f(x,y,z)dvlim∑f(x_i,y_i,z_i)∆v_i.

(5)

V ^{λ→0i0}

Определениетройногоинтегралапредполагает,чтоинте-грируемаяфункцияf(х,у,z)являетсяограниченной.

Всоответствиисопределением,если

f(x,y,z)1,тогда

тройнойинтегралравенобъемуцилиндрическоготела,приве-денногонарис.4.Тройнойинтегралобладаетсвойствами,ана-логичнымисвойствамдвойногоинтеграла.Рассмотримвычис-лительнуюформулутройногоинтеграла.Тройнойинтегралне

зависитотспособаразбиенияVнаnобъемов.РазбиениеVосуществляемплоскостями,параллельнымикоординатнымплоскостям.ПослевыбораточкиP(х_i,у_i,zi)(произвольно)исо-

n−1

ставленияинтегральнойсуммы

∑^f(x_i^,y_i^,z_i^)∆x_i^∆y_i^∆z_i^,ее

i0

слагаемыеперераспределимследующимобразом:

n−1

n₁ n₂ n₃

∑^f(x_i^,y_i^,z_i^)∆x_i^∆y_i^∆z_i

^∑^∆x_i∑^∆y_j∑^f(x_i^,y_j^,z_k^)∆z_k^.

(6)

i0

i0

j0

k0

Внутреннеесуммированиепроизводитсяпоэлементарнымобъемам,содержащимсяввертикальныхстолбикахсфиксиро-

ваннымоснованием

∆x_i∆y_j,(∆x_i∆y_j

• общиемножителиво

внутреннейсумме)которыепересекаютVотповерхности

zz₁₍x,y)

идо

zz₂₍x,y)

(рис.4).Промежуточноесумми-

рованиев(6)осуществляетсяпостолбикам,которыесгруппи-рованывплоскости,параллельныеy0z.Этистолбикинаходятся

впределахот

yy₁₍x)

идо

yy₂₍x)

(рис.4).Вэтомслучае

фиксированнымиявляются

∆x_i,которыевыносятсязазнак

суммыкакобщиймножитель.Внешнеесуммированиевключа-етвсебясуммированиеплоскостейсосгруппированнымистолбиками.Этиплоскостипараллельныy0z.Указанныеплос-костинаходятсявпределах[a,b].Индексkвформуле(6)опре-деляетместоположениеэлементарногообъемавнутристолби-ка.Индексjопределяетместоположениестолбикавнутриплоскостисосгруппированнымистолбиками,параллельнойплоскостиy0z.Индексiопределяетместоположениеуказанныхплоскостейсосгруппированнымистолбиками.

Врезультатепредельногоперехода

λmax∆d_i→0

при

условиинепрерывностиподинтегральнойфункцииинтеграль-наясуммастремитсякконечномупределу,илизначениютрой-ногоинтеграла.

Такимобразом,тройнойинтегралможетбытьзаписанвследующемвиде

b

_∫∫∫f(x,y,z)dv_∫dx

y₂₍x)

∫

z₂₍x,y)

dy _∫f(x,y,z)dz.

(7)

V a y₁₍x)

z₁₍x,y)

Справав(7)записанповторныйинтеграл,которыйестьсо-вокупностьтрехопределенныхинтегралов.Внутреннийинте-гралпопеременнойz,прификсированныхx,y.Промежуточ-ный—попеременнойyприxфиксированном,ивнешний—попеременнойx.

Методывычисленияопределенныхинтеграловрассмотре-нывконтрольнойработепотеме«Определенныйинтеграл».

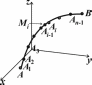Дананепрерывнаяфункциятрехпе-ременныхf(х,у,z)(рис.5),котораяопределенаналинииAB.ЛинияABпроизвольнымспособомразделенана

nчастичныхдугдлиною

∆l_i

(где

i=1,…n).Внутрикаждойдуги

∆l_i

выбирается произвольным образом

Рис.5.

точка

M(x_i,y_i,z_i),вкоторойвычис-

ляетсязначениефункцииf(х_i,у_i,z_i)и

n−1

^{составляетсяинтегральнаясуммавидаσ}∑^f(x_i^,y_i^,z_i^)∆l_i^.

i0

Еслипотребовать

λmax|∆l_i|→0,тогдачислослагае-

мыхвсумменеограниченновозрастает.Длянепрерывныхфункцийпределсуммыравенконечномучислу.