Решение:

Продифференцируемобечастипервогоуравненияпопе-

ременнойt:



^dx

_{ }(4x2y)^

или

x^4x^2y^.

_dt_

Чтобыполучитьдифференциальноеуравнениевторогопорядкаотносительнофункциих(t),подставимвместоуеевы-ражениеизвторогоуравнениясистемы:

x^4x^2(хy)

или

x^4x^2х2y. (5)

Изпервогоуравнениясистемынайдем2у:

2ух^4х

иподставимвуравнение(5):

x^4x^2хх^4х

или

x^5х^6х0.

Полученноеуравнениеявляетсялинейнымоднородным

уравнениемспостояннымикоэффициентами.Находимкорнисоответствующегохарактеристическогоуравнения

2t

3t

k^25k60,

k_12,

k_23.Тогда

x_1e

иx_2e,

а xc₁

• x₁

c₂

• x₂

c₁

• e^2tc₂

• e^3t.

Однаизнеизвестныхфункцийх(t)найдена.Длянахожде-

ниявторойфункцииу(t)воспользуемсясоотношением,полу-

ченнымранее:

_ух^4х_.

2

Тогда

x^2c₁

• e^2t3c

• e^3t,

2

x^4х2c₁

• e^2t3c₂

• e^3t4c

• e^2t4c

• e^3t2c

• e^2tc

• e^3t,

1

yc

• e^2t^1c

• 1

  2

  2

  e^3t.

1 ₂₂

Общеерешениеданнойсистемыимеетвид

^xc

• e^2tc

• e^3t,

 ¹

^ 2t

2

¹ 3t

_yc_1e

 c_2e.

2

Задачидляконтрольныхзаданий

1–10.Найтиобщеерешение(илиобщийинтеграл)данныхдифференциальныхуравненийпервогопорядка:

1. а)

2ху^у^21;

^y

б)ху^уln_{ };

^x

в)ху^xу1.

2. а)

y^2у2x1x^2;

б)ху^у

х^2у^2;

в)(1х²)у^2xу1x^2.

3. а)

б)

в)

у^xуxу^2;

у^24ху4х^2у0;

х(х1)у^2xу1.

4. а)

х^2уу^21;

б)у^

2

у_6у

_х2 _х

6;

в)

5. а)

у^^3ух.

х

ху^уу^2;

б)у^

у2х_;

ху

в)ху^

у

х1

х.

6. а)

б)

у^ху^22ху;

у^^х^у;

у х

в)у^у(2х3)е^х.

7. а)

ху^у30;

б)у^

у3х_;

х3у

в)2ху^у3х^2.

8. а)

б)

в)

9. а)

б)

у^3х^2ух^2;

у

ху^хе^ху0;

х^2у2ху3.

уу^^12х;

ху

х^2уу^22ху0;

в)у^уtgx

1 _.

cosх

10. а)

б)

(1х²)у^хуxy^2;

х^2уу^2ху;

в)у^2

^ух^22х.

х

11–20.Найтичастноерешениеданногодифференциально-гоуравненияпервогопорядка,удовлетворяющееданномуна-чальномуусловию:

11.

ху^2

хуу,

4

у(1)1.

12.

13.

у^4х^3ух³е^ху^2,

уу^у²ctgxcosx,

у(0)8.

у_^π_1.

 

14.

2ху^у

3x²

,

y

^2

у(1)2.

15.

х^2у2xyу^2,

у(1)1.

16.

ху^4ух² у,

у(1)1.

17.

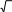2ху^3у(20х^212)у^3,

у(1) ¹ .

22

18.

у^уtgxу^2cosx0,

у(0)1.

19.

2ху^у^1,

хy

_х2

у(2)^1.

2

20.

у^ху2xе^-2

у^2,

у(0)1.

21–23.Найтиобщеерешениедифференциальногоурав-нениявторогопорядка:

21.

22.

23.

24.

25.

26.

(1у)у^5(у^)^20.

(1х²⁾у^ху^.

у^tgy2(у^)^2.

ху^y^х1.

(у^)^22уy^0.

ху^y^^10.

х

27.

у^2

^ух^2.

х

28.

29.

30.

1(у^)^2уy^0.

х^4ух^3y4.

(х^21)у^2хy^х^3.

3140.Найтичастноерешениедифференциальногоурав-нениявторогопорядкаспостояннымикоэффициентамиспра-войчастьюспециальноговида,удовлетворяющееданнымна-чальнымусловиям:

31.

32.

33.

34.

35.

36.

37.

у^4у^13у26х^23х,

у^2у^2е^х(sinxcosx),

у^5у^6у12cos2х,

у^4у^12у8sin2х,

у^у^2уe^x(2х2),

у^5у^15х^24х,

у^4у^5уe^xх,

у(0)1,

у(0)0,

у(0)1,

у(0)0,

у(0)2,

у(0)1,

у(0)^1,

2

у^(0)0.

у^(0)0.

у^(0)3.

у^(0)0.

у^(0)1.

у^(0)^2.

5

у^(0)0.

38.

39.

40.

у^2у^уe^2x(х1),

у^2у^5у10х^27х8,

у^4у^3у2e^x,

у(0)2,

у(0)0,

у(0)2,

у^(0)0.

у^(0)0.

у^(0)1.

41–50.Найтиобщеерешениесистемылинейныхдиффе-ренциальныхуравненийспостояннымикоэффициентамипутемсведенияеекодномууравнениювторогопорядка:

41.

^dx4x6y,

^dt

^dy

42.

^dx5x4y,

^dt

^dy



dt

4x2y.



dt

2x3y.

43.

^dx3xy,

^dt

^dy

44.

^dx6x3y,

^dt

^dy



dt

8xy.



dt

8x5y.

45.

^dxx5y,

^dt

^dy

46.

^dx3x2y,

^dt

^dy



dt

x3y.



dt

2x8y.

47.

^dx4x6y,

^dt

^dy

48.

^dx5x8y,

^dt

^dy



dt

4x2y.



dt

3x3y.

49.

^dxx5y,

^dt

^dy

50.

^dx7x5y,

^dt

^dy



dt

7x3y.



dt

4x8y.