Рекомендациипорешениютиповыхзадач

Задача1.Найтиобщеерешение(илиобщийинтеграл)данныхдифференциальныхуравнений:

а)хуу^1х^2,

в)4х3уу^(2у3х)0,

с)ху^2ух^2.

Решение:

а)Запишемуравнениеввидеуравнения,разрешенного

относительнопроизводной,т.е.ввиде

у^

f(x,у).

Вданномслучае,поделивобечастиуравнениянаполучаем

ху,

2

_{у}1х

ху

_1х 1_.

2

х у

Праваячастьуравненияестьпроизведениедвухфункций,каждаяизкоторыхзависиттолькоотоднойпеременной.Этозначит,чтоданноеуравнениеявляетсяуравнениемсразделяю-щимисяпеременными.Разделимпеременныеследующимидей-ствиями:

у^^dy,

dy_1x 1_,

ydy

1x²

dx.

2

dx dx x y x

Получиливрезультатеуравнениесразделеннымипере-менными,обечастикоторогоинтегрируем:

уdy

1x²

dx,

уdy

^1x^dx,

  _x

dx

 





^x 

_y2 _x2

_уdy_x

_xdx,

ln2

x c,

2

y^2x²

2

ln

xc.

Мыполучилисоотношениемеждух,уипроизвольной

постояннойс,котороеназываетсяобщиминтегралом.

в)Разрешимуравнениеотносительнопроизводнойу:

_{у}4х3у

2у3х

или

у^^{4х3у.} (1)

3х2у

Праваячастьэтогоуравнения

f(x,у)^4x3y

3x2y

являетсяоднороднойфункциейнулевогопорядкаотносительносвоихаргументов,таккакудовлетворяетследующемуусловию:

Всамомделе,

f(tx,ty)

f(x,y).

_{f(tx,ty)}4(tx)3(ty)

3(tx)2(ty)

_=t(4x3y)t(3x2y)

₌₄x3y_

3x2y

f(x,y).

Отсюдаследует,чтоуравнение(1)являетсяоднородным.Од-

нородноеуравнениерешаютподстановкойНайдемуиподставимвуравнение(1):

y^u^xu,

u^yx

или

yux.

u^xu^4x3ux,

3x2ux

u^x^43uu,

32u

u^xu^{x(43u),}

x(32u)

_{ux}43uu(32u)_,

32u

2

_{ux}2u6u4_.

32u

Получившеесяуравнениеоказываетсяуравнениемсразделяю-щимисяпеременными.Разделяемпеременные:

du 2u^26u4

x ,

(32u)du

_dx_,

dx 32u

2u^26u4 ^x

послечегоинтегрируем:



32u

dx

du_ ,

2u^26u4 ^x

2

1

_2

4u6_du

2u^26u4

=¹_

2

d(2u6u4)₌

2u^26u4

=^1ln2u²²

dx

6u4c_{1, x}

ln

xc_1.

Получаемобщийинтеграл:

^1ln2u^26u4ln2

xlnc,где

lncc₂

• c_1.

Послепотенцированияобщийинтегралприметвид

2u^26u4

1 _.

_c2_x2

Вернемсякстаройфункцииу,подставиввместоu ^у:

х

^у2 ^у

1

2_{ }6

4

_х_ х

_с2_х2

или

2у^26ху4х^2^1.

_с2

с)Вданноеуравнениенеизвестнаяфункцияуиеепроиз-

воднаяувходятвпервойстепени.Отсюдаследуетвывод:уравнениеявляетсялинейным.Будемискатьрешениелинейно-гоуравненияввидепроизведениядвухпоканеизвестных

функцийu(x)иv(x),т.е.

уuv.Найдемпроизводную

у^u^vuv^

иподставимвуравнение(2):

x(u^vuv^)2uvx^2,

xu^vxuv^2uvx^2,

xu^v(xuv^2uv)x^2,

xu^vu(xv^2v)x^2.

Длянахожденияфункцииv(x)положим:

xv^2v0.

Найдемчастноерешение(дляэтогоположимс=0)этого

уравнениясразделяющимисяпеременными:

x^dv2v,

dv_{2dx,}

dx v x

dv dx 1

_v2_x,

lnv2lnx,

v .

_x2

Длянахождениядругойфункцииu(x)унасполучается

уравнение:

xu^vx^2,

xu^1

_x2

x^2,

u^x^3,

^dux^3,dx

dux³dx, _du_x³dx,

4

u^x

c.

4

Общеерешениеданногоуравнения(2)будетиметьвид

_x4

^1 x² c

yuv^{}c^{}  .

4

x

  ²

 

_{4 x}2

Задача2.Найтичастноерешениедифференциальногоуравнения

2ху^у

3х²

,

у

удовлетворяющееначальномуусловию

у(1)2.

Решение:УравнениеБернуллиимеетвид

у^р(х)уq(x)y^n,

n0,

n1.

Данноеуравнениеможнозаписатьввиде

2

у^^у

2х

_3х

2х

_у1_,

поэтомуделаемвывод:данноеуравнениеявляетсяуравнением

Бернулли.Егоможнорешатьтемжеметодом,чтоилинейное

уравнение.Будемискатьобщеерешениеввиде

у^u^vuv^,

уuv:

u^vuv^^uv

2x

 

3x _,

2uv

3

u^vu_v^

v_ x _,

_ 2x_

2uv

v^^v

0,

dv_dx_{, }dv_1_dx_,

2x v 2x

v 2 x

lnv^1lnx,

2

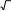v x

• однуфункциюнашли.

u^

x ^3x ,

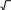
2u x

du_3_,

dx 2u

2udu3dx, _2udu_3dx,

u^23xc

или

u 3xc.

Общеерешениеуравненияприметвид

yuv

3xc x

3x^2cx.

Чтобынайтичастноерешениеуравнения,нужнонайтизначениеконстантыс.Дляеенахожденияподставимвобщеерешениех=1иу=2:

2 31с1

3с,

43с,с=1.

Подставиввобщеерешениезначениес=1,получаемча-

стноерешениеу

3х^2х.

Задача3.Найтиобщеерешениедифференциальногоуравнениявторогопорядка