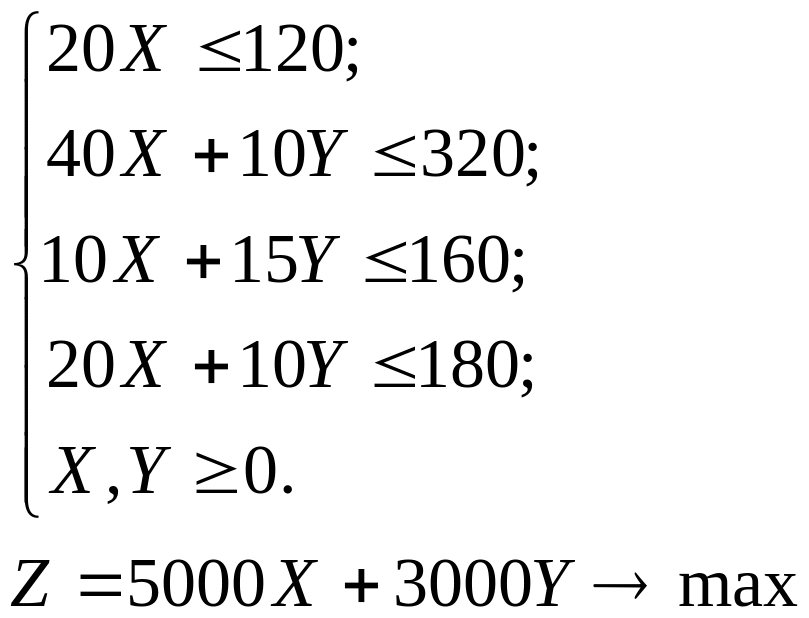Элементы линейного программирования и транспортная задача рабочая тетрадь студента (-ки) _____ курса ___________________________________ факультета

____________________________________________________________________

специальности

Группы № ________

УДК 519.852

ББК 22.18

Л59

Ольга Владимировна Морозова;

	Линейное программирование и транспортная
Л59	задача : рабочая тетрадь / О. В. Морозова, – 104 с.
	Рабочая тетрадь входит в серию методических разработок, способствующих овладению студентами теоретическими основами материала и появлению у них навыков решения задач по основ – ным разделам курса математики. Предназначена для использования во время практических занятий и в качестве задачника для самостоятельной работы и контроля знаний студентов.
	УДК 519.852 ББК 22.18

Глава 1. Линейное программирование

1.1. Общая задача линейного программирования

Модели линейного программирования используются для определения плана производства. Эти возможности обобщаются для случая, когда закупка готовой продукции для последующей реализации может оказаться для производителя предпочтительнее, чем использование собственных мощностей. Рассматривается также задача производственного планирования, учитывающая динамику спроса, производства и хранения продукции. Наиболее часто такие задачи возникают на уровне агрегированного планирования и оперативного управления микроэкономическими объектами.

Общая постановка задачи планирования производства: необходимо определить план производства одного или нескольких видов продукции, который обеспечивает наиболее рациональное использование имеющихся материалов, финансовых и других видов ресурсов. Такой план должен быть оптимальным с точки зрения выбранного критерия – максимума прибыли, минимума затрат на производство и т.д.

Пусть дана система m неравенств с n – неизвестными.

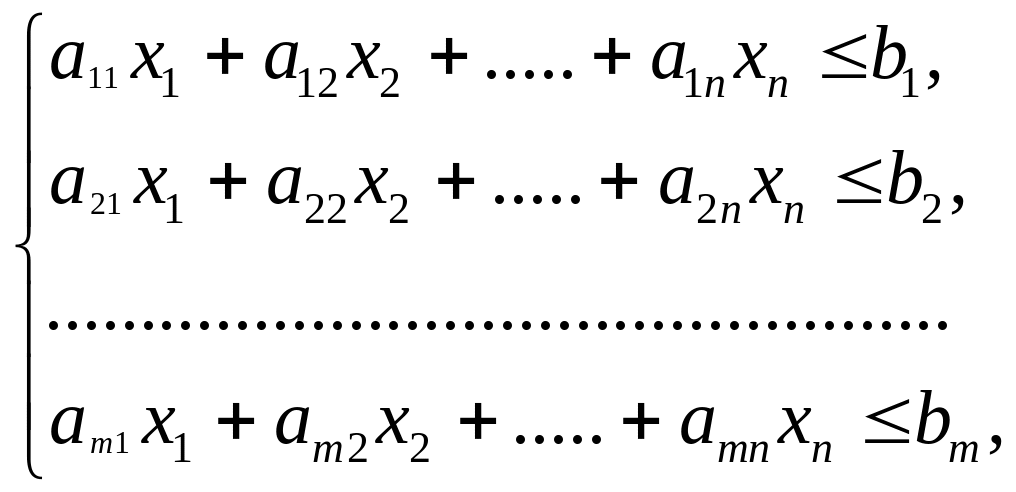(1)

х_1,2 0 должно быть всегда (по смыслу экономических задач).

– линейная функция.

Необходимо найти такое решение системы Х = (х₁, х₂, …., х_n), при котором линейная функция Z принимает оптимальное, т. е. mах (min) значение.

Если система ограничений состоит из одних неравенств, то задача называется стандартной; если же из уравнений, то задача называется канонической. Чтобы перейти от стандартной формы к каноническому виду вводят дополнительные неотрицательные переменные со знаком «+», если знак неравенства «≤» и со знаком «–» , если знак неравенства «≥», т. е. неравенство можно заменить выражением

.

Решение экономической задачи можно разбить на три этапа:

1. построение экономико – математической модели;

2. нахождение оптимального решения;

3. практическое внедрение полученных результатов в народном хозяйстве.

Чтобы составить математическую модель задачи линейного программирования необходимо:

• ввести обозначения переменных;

• исходя из цели экономических исследований составить целевую функцию;

• учитывая ограничения в использовании экономических показателей задачи и их количественные закономерности, записать систему ограничений.

Пример. Фермер на своем участке выращивает огурцы и помидоры. Чтобы не потерять урожай, он использует азотные, калийные, фосфатные удобрения и навоз. Чтобы удобрить один гектар огурцов ему необходимо 20 ед. азотных удобрений, 40 – калийных, 10 – фосфатных, 20 – навоза; помидоров – 10 – калийных, 15 – фосфатных, 10 – навоза. Его запасы удобрений следующие: азотных – 120, калийных – 320, фосфатных – 160, навоза – 180. Прибыль с 1 га площади, засаженной огурцами, – 5000 у. д. е., а помидорами – 3000 у. д. е. Сколько гектаров огурцов и помидоров необходимо обработать для получения максимальной прибыли.

Решение. В качестве переменных выберем площади, занимаемые под посадки огурцов (переменная Х) и помидоров (переменная Y). Обозначим используемые ресурсы: азотные удобрения – S₁, калийные – S₂, фосфатные – S₃, навоз – S₄. Тогда данные условия задачи можно свести в наглядную таблицу:

Ресурсы	Затраты удобрений, ед/га		Запасы
	Х	Y
S1	20	0	120
S2	40	10	320
S3	10	15	160
S4	20	10	180
Прибыль	5000	3000

На основании вышеизложенного математическая модель задачи будет выглядеть следующим образом: