ω

U_з

ΔU

U_в

U_д

Д

МУ

У

-U_тг

ТГ

Рис. 2 Структурная схема САУ

М_с

H_мс(P)

-Δω

Н_му(P)

Н_д(P)

H_у(Р)

U_{з Δ}U U_в U_д ω

g y

-U_тг

H_тг(P)

Рис.3 Функциональная схема САУ

3. Определение передаточных функций звеньев и их параметров

3.1 Двигатель.

Двигатель представляет собой электромеханическую систему которая преобразует электрическую энергию в механическую. ДПТ НВ может быть как колебательным звеном так и апериодическим второго порядка.

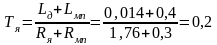
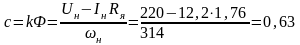
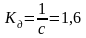
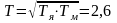
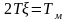
Так как коэффициент дэмфирования 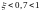то двигатель будет колебательным звеном с ярко выраженными свойствами.

Т_я – электрическая постоянная цепи якоря, Т_м – электромеханическая постоянная времени.

3.2. Магнитный усилитель

Магнитный усилитель - это статический аппарат, предназначенный для управления величиной переменного тока посредством слабого постоянного тока. Применяется в схемах автоматического регулирования электродвигателей переменного тока.Это апериодическиое звено.

3.3 Тахогенератор

Тахогенератор - пропорциональное звено по этому передаточная функция имеет следующий вид:

3.4 Усилитель

Усилитель - предназначенный для усиления входного сигнала до уровня, достаточного для срабатывания исполнительного механизма.

Усилитель - пропорциональное звено с коэффициентом усиления k_у.

Определит коэффициент усиления k_у можно найти исходя из статической ошибки

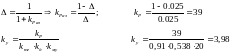
Передаточная функция

4. Составление уравнения движения САУ

4.1 Определение передаточной функции разомкнутой САУ

4.2 Определение передаточную функцию замкнутой САУ

По заданию

По возмущению

4.2 Составление уравнения САУ

На основании передаточных функций по задающему и возмущающему воздействиям замкнутой системы, записывается уравнение движения этой системы, которое представляет собой дифференциальное уравнение, связывающее выходную координату с задающим и возмущающим воздействиями.

Полное уравнение системы в общем виде в операторной форме имеет вид:

,

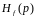где и - передаточные функции по заданию и по возмущению, соответственно.

5. Исследование системы на устойчивость

5.1 По методу Гурвица

Характеристическое уравнение САУ имеет вид

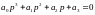
Все члены характеристического уравнения положительны

Составим определитель второй степени этого уравнения. Для устойчивости не обходимо и достаточно, чтобы он был больше нуля

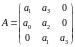
Так как Δ₂< 0 можно сделать вывод что САУ неустойчивая.

5.2 Частотный критерий (критерий Найквиста)

Запишем уравнение АЧХ, для разомкнутой системы

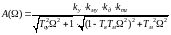
Подставим числа из частотного диапазона в функцию А(Ω)

Запишем уравнение ФЧХ, для разомкнутой системы

Запишем уравнение, для построения АФХ

-на Re оси : U = А(Ω) ∙ cos Ψ(Ω)

-на Im оси : V = А(Ω) ∙sin Ψ(Ω)

Рис.4 Амплетудно-фазовая характеристика звена

Так как АФХ охватывает точку с координатой (-1,0), то исходя из критерия Найквиста система не устойчива.

6. Определение коеффицента усиления усилителя сау при котором система устойчива.

Составляем уравнение устойчивости для разомкнутой системы

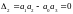
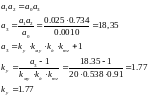
Проверка системы на усточивости при измененном коэффеценте усиление с помощью частоного критерия Найквеста.

Ω	A(Ω)	Ψ(Ω)	U	V
0	18,3	0	18,3	0
0,5	17,2	-0,35	16,2	-5,98
1	14,9	-0,64	11,9	-9,01
1,5	12,5	-0,86	8,20	-9,55
3	7,76	-1,22	2,60	-7,31
5	4,83	-1,46	0,49	-4,81
8	2,90	-1,68	-0,33	-2,88
12	1,73	-1,93	-0,61	-1,61
15	1,25	-2,14	-0,67	-1,05
20	0,90	-2,56	-0,75	-0,49
25	0,96	-3,05	-0,96	-0,08

Рис.5 Амплетудно-фазовая характеристика звена

При измененном коэффиценте усиления k_у=1,77 АФХ не охватывает точку с координатой (-1,0), то исходя из критерия Найквиста система оказалась устойчива.

Выводы:

Даная система автоматического управления в результате математического исследования оказалась неустойчивой. Это подтвердили два метода определения устойчивости системы: Гурвица и частотного критерия Найквиста. Для того чтобы система была работоспособной необходимо ее приведение к устойчивому состоянию за счет изменения параметров системы таких как коэффициент усиления какого либо звена, постоянных времени, а так же скорости передвижения координатного стола. В результате изменения коэффицета усиления усилителя от заданого значения удалось установить значение при котором система устойчива k_у=1.77 в отличии от заданного k_у=3.98 . На наглядном реальном примере четко видно значение критериев устойчивости САУ Гурвица и Найквиста.

7. Список литературы

1. Попович М.Г., Ковальчук О.В. Теория автоматического управления.- К.: Лыбидь,1997. – 544с.

2. Динамика элементов автоматизированного электропривода: Учеб. пособие / Р.П. Герасимяк. – Киев: -УМК У, 1989.,-100 с.

3. Попов Е.П. Теория линейных систем автоматического регулирования и управления. М.: Наука, 1989,-304 с.

4. Теория автоматического управления. Ч.1. Теория линейных систем автоматического управления / Н.А. Бабаков, А.А. Воронов и др;. Под ред. А.А. Воронова. М.: Высш. шк., 1986, -376 с.