Прикладна механіка
Частина 2.
1. Структурний аналіз плоских механізмів
Мета структурного аналізу: вивчення будови механізму; визначення ступеня його рухомості; побудова структурної схеми та визначення послідовності приєднання структурних груп, їх класу та класу механізму в цілому.
Вихідні дані: кінематична схема механізму.
1.1. Ступінь рухливості механізму
Свідоме виконання завдання на курсовий проект вимагає від студента чіткого розуміння роботи всієї машини в цілому. Тому, приступаючи до виконання завдання, слід перш за все розібратися в структурі досліджуваної системи, тобто визначити число кінематичних пар, з'ясувати їх характер і підрахувати число рухомих ланок.
Після такого розбору можливо з'ясувати метод утворення механізму, а разом з тим і схему передачі руху від провідної ланки до робочого органу.
У завданнях до курсового проекту наведені плоскі важільні механізми. Плоским механізмом називають механізм, усі ланки якого, рухаються в одній площині або в паралельних площинах [1].
У плоскому механізмі заздалегідь накладені загальні зв'язки позбавляють кожну з ланок трьох мір свободи, а саме: обертання навколо двох координатних осей, які лежать в площині руху механізму і ковзання уздовж осі, перпендикулярної до цієї площини. Тому кінематичні пари можуть накласти на відносний рух ланок, які утворюють кінематичну пару, або одну, або дві умови зв'язку. Таким чином, в плоскому механізмі можуть бути тільки наступні пари:
а) вищі кінематичні
(наприклад, профілі зубчатих циліндрових
коліс, що сполучаються, або система
профіль кулачкової шайби - штовхач.)
Число цих пар механізму позначатимемо
б) обертальна
(шарнір) або поступальна (повзун) в тих
парах, що направляють рух. Число таких
пар механізму позначатимемо
.
У завданнях на проект приведені механізми, в яких пасивні зв'язки відсутні. Тому, підрахувавши число ланок механізму та числа і кінематичних пар, можливо, за структурною формулою П. Л. Чебишева для плоского механізму, підрахувати його ступінь рухливості:
(1.1)
У
приведеному записі
означає тільки число всіх рухомих ланок
механізму; стійка, отже, приведеною
формулою не враховується. Точно також
при підрахунку ступеню рухливості
системи, що має в своєму складі кулачковий
механізм, звичайно в число ланок не слід
включати ролик. За цієї умови у всіх
завданнях на проект матимемо W = 1, тобто
положення механізму визначається
завданням одного параметру, наприклад,
кутової координати ланки, закон руху
якої задається.
При підрахунку
ступеня рухливості кулачкового механізму
з урахуванням ролика одержуємо W = 2 -
факт добре відомий і такий, що легко
пояснюється теорією. Проте для спрощення
завдання аналізу і синтезу механізмів
не слід брати до уваги наявність ролика
на першому етапі дослідження, оскільки
він не міняє характер руху робочого
органу (ланки, що виконує технологічний
процес). Головним завданням ролика є
заміна тертя ковзання, для якого
коефіцієнт тертя досягає
,
на тертя кочення з коефіцієнтом
,
що на порядок нижче.
Для визначення ступеня рухливості просторового механізму використовується загальна формула Сомова – Малишева [1]:
,
(1.2)
де
- кількість кінематичних пар відповідного
класу в механізмі.
1.2. Метод утворення плоских механізмів
У всіх завданнях на проект указано нерухому ланку (під штрихуванням) і безпосередньо пов'язану з нею, обертальною або поступальною парою, провідну ланку (стрілка показує напрям руху).
Сукупність вказаних
двох ланок утворює так званий нульовий,
або початковий, механізм (механізм l-го
класу). Легко переконатися, що ця система
володіє одним ступенем рухливості.
Насправді, тут
;
і тому за формулою (1.1) отримуємо:
Складніші схеми механізмів отримують послідовним приєднанням до початкового механізму (механізму l-го класу) ряду кінематичних ланцюгів. Для того, щоб новий складний механізм також мав одну ступінь рухливості, потрібно, щоб ці послідовні нашарування не змінювали ступінь рухливості початкового механізму. Це означає, що ступінь рухливості ланцюгів, які приєднуються, повинен дорівнювати нулю. Такі прості ланцюги, ступінь рухливості яких дорівнює нулю, називають нормальними ланцюгами, або групами Л. В. Ассура. Число ланок і число кінематичних пар у таких групах, як і способи їх побудови різні.
У завданнях зустрічаються тільки групи двох типів: двох - і чотирьох ланкові, які приєднуються вільними елементами кінематичних пар до механізму (або структурні видозміни цих двох типів).
Механізм, утворений нашаруванням одних тільки двох ланкових груп, називають механізмом 2-го класу; механізм, до складу якого входять і чотирьох ланкові групи, називають механізмом 3-го класу. Останні одержують з нормальних груп спрощенням їх структури, яке полягає в тому, що одну ланку з двома нижчими кінематичними парами замінюють однією вищою кінематичною парою. Така заміна не міняє ступені рухливості нормального ланцюга. Насправді, ланка з двома нижчими парами накладає на систему один зв'язок:
.
Вища кінематична пара також накладає один зв'язок і, отже, не тільки нормальний ланцюг, але і його видозміна володіє нульовим ступенем рухливості. Таким чином, з погляду структури двох ланкова група, що складається з двох ланок і трьох нижчих кінематичних пар, може бути замінена групою, що складається з однієї ланки, одного елементу вищої кінематичної пари і одного елементу нижчої пари. Чотирьох ланкова група, що складається з чотирьох ланок і шести нижчих кінематичних пар, може бути з погляду структури замінена ланцюгом, що складається з трьох ланок, чотирьох нижчих кінематичних пар і однієї вищої пари.
На рис. 1, зображена схема механізму двигуна з компресором, а на рис. 2 - відповідно його структурна схема.
Загалом, відмінність структурної схеми від кінематичної полягає в тому, що структурні видозміни замінені відповідними нормальними групами, в яких додаткові ланки позначені буквами замість цифр, а поступальні пари замінені умовно обертальними.
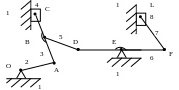
Рисунок 1. Схема механізму двигуна з компресором
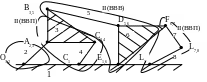
Рисунок 2. Структурна схема механізму двигуна з компресором
Таким чином, легко встановити, що механізм, показаний на рис. 2, утворений послідовним приєднанням трьох двох ланкових груп таким чином:
а) до нульового механізму (1-2) приєднана група 3, 4;
б) до ланок 3 і 1 приєднана група 5, 6;
в) до ланок 6 і 1 приєднана група 7, 8.
1.3. Побудова структурної схеми механізму
Методи дослідження механіки машини знаходяться в прямій залежності від типу напластованих груп ланок із нульовим ступенем рухомості (групи Л. В. Ассура). Отже, в завданнях зустрічаються двох- та чотирьох- ланкові групи які досліджуються різним чином. Тому, приступаючи до проектування механізму, кінематична схема якого наведена в завданні, для з'ясування методу дослідження механіки цього механізму, слід заздалегідь накреслити його структурну схему. Найбільш простим є метод прямого вивчення структури, який починається з нульового механізму (механізму l-го класу) і йде у порядку нашарування груп Л. В. Ассура:
1). Виділяється нульовий механізм (механізму l-го класу).
2). Оскільки групи Ассура повинні приєднатися своїми вільними елементами до різних ланок наявного механізму то напластована група не може бути приєднана тільки до однієї ланки. У останньому випадку вона утворила б одне тверде тіло з цією ланкою. Таким чином, перше нашарування може бути приєднано тільки до стійки і провідної ланки. Тому двох ланкова група кожним вільним елементом приєднується до іншої ланки, а три вільні елементи чотирьох ланкової групи приєднуються двома елементами до однієї ланки і одним - до іншого.
3). Наступна нормальна група може бути приєднана до схеми, що утворилася, подібним же чином, тобто вільними елементами до ланок нульового механізму і першого нашарування (тільки не до однієї ланки). Аналогічно всі наступні нашарування приєднуються вказаним способом до ланок нульового, механізму і раніше приєднаних груп.
Нашарування у вигляді двох ланкових груп знаходяться легко, оскільки дві ланки, з яких кожне пов'язане з раніше приєднаними групами, повинні бути пов'язані безпосередньо один з одним. Якщо така група відсутня, то в завданнях слід шукати чотирьох ланкову групу так: вибираючи дві ланки, пов'язані з ланками вже існуючої схеми, але не сполучені між собою безпосередньо треба відшукати між ними ще дві ланки так, щоб в групі, що утворилася з чотирьох ланок, було шість нижчих кінематичних пар.
4). Видозміни груп Л. В. Ассура, що зустрічаються, замінюються нормальними групами шляхом заміни вищої кінематичної пари додатковою ланкою з двома нижчими парами.
5). Для більшої одноманітності структурної схеми поступальні пари умовно замінюються обертальними. При такій заміні число умов зв'язку не міняється, оскільки поступальні пари, так як і обертальні, теж накладають по два зв'язки на відносний рух ланок.
При побудові структурної схеми для уникнення помилок і полегшення читання креслення рекомендується:
а) зберігати на ній ті ж буквені позначення в місцях зчленування ланок і ту ж нумерацію ланок і кінематичних пар, які є на заданому кресленні;
б) двох членні ланки (ланки, що включають тільки два елементи кінематичних пар) зображати відрізками прямих, трьох членні – у вигляді заштрихованих трикутників, чотирьох членні - у вигляді заштрихованих чотирикутників і т.д.
1.4. Послідовність структурного аналізу
Структурний аналіз проведемо на прикладі механізму двигуна з компресором, кінематична схема якого зображена на рис.1. у такій послідовності:
1). Визначається кількість рухомих ланок механізму
1 – нерухома ланка, стійка;
2 – кривошип;
3 – шатун;
4 – повзун;
5 – шатун;
6 – коромисло;
7 – шатун;
8 – повзун.
2). Розписуються кінематичні пари, визначається їх клас і вид:
(1 – 2) - обертальна
кінематична пара п’ятого класу –
,О;
(2 – 3) - обертальна кінематична пара п’ятого класу – ,О;
(3 – 4) - обертальна кінематична пара п’ятого класу – ,О;
(4 - 1) – поступальна кінематична пара п’ятого класу – ,П;
(3 – 5) - обертальна кінематична пара п’ятого класу – ,О;
(5 – 6) - обертальна кінематична пара п’ятого класу – ,О;
(6 – 1) - обертальна кінематична пара п’ятого класу – ,О;
(6 – 7) - обертальна кінематична пара п’ятого класу – ,О;
(7 – 8) - обертальна кінематична пара п’ятого класу – ,О;
(8 - 1) – поступальна кінематична пара п’ятого класу – ,П.
Буква О означає обертальну кінематичну пару п’ятого класу, а буква П - поступальну кінематичну пару п’ятого класу.
3). Вираховується ступінь рухливості механізму за формулою 1.1:
Ступінь рухливості
показує, що для роботи механізму потрібен
один двигун.
4). Визначаються ланки, які вносять до механізму надмірні зв’язки:
ланки, які вносять до механізму надмірні зв’язки у наведеному прикладі – відсутні.
5). Визначаються ланки, які вносять до механізму надмірні ступені рухливості:
ланки, які вносять до механізму надмірні ступені рухливості у наведеному прикладі – відсутні.
6). Проводиться заміна кінематичних пар вищого (4го) класу на кінематичні пари нижчого (5го) класу:
кінематичні пари вищого (4го) класу у наведеному прикладі – відсутні.
7). Будується структурна схема механізму (рис.2) за правилами:
а) нерухому ланку (стійка) зображують горизонтальною прямою лінією зі штриховкою;
б) рухомі ланки зображують:
- прямою лінією, якщо вони з’єднуються з іншими ланками двома кінематичними парами;
- трикутником, якщо вони з’єднуються з іншими ланками трьома кінематичними парами;
- чотирикутником і т.д., відповідно до кількості кінематичних пар.
в) всі кінематичні пари зображують кружечками і позначають відповідними буквами латинського алфавіту з цифровими індексами:
- обертальна пара – двома цифрами – номерами тих ланок, які входять у пару;
- поступальна пара – однією цифрою, номером тієї ланки, яка є направляючою для повзуна.
8. Виділяються групи з нульовим ступенем рухомості, починаючи з найвіддаленішої від приводу механізму ланки та групи нижчого класу (рис.2). Визначається клас і вид виділених груп.
9. Записується структурна формула механізму:
10. Визначається клас механізму:
у цілому, даний механізм - ІІго класу (визначається за класом вищої групи).
1. Структурний аналіз плоских механізмів
Мета структурного аналізу: вивчення будови механізму; визначення ступеня його рухомості; побудова структурної схеми та визначення послідовності приєднання структурних груп, їх класу та класу механізму в цілому.
Вихідні дані: кінематична схема механізму.
1.1. Ступінь рухливості механізму
Свідоме виконання завдання на курсовий проект вимагає від студента чіткого розуміння роботи всієї машини в цілому. Тому, приступаючи до виконання завдання, слід перш за все розібратися в структурі досліджуваної системи, тобто визначити число кінематичних пар, з'ясувати їх характер і підрахувати число рухомих ланок.
Після такого розбору можливо з'ясувати метод утворення механізму, а разом з тим і схему передачі руху від провідної ланки до робочого органу.
У завданнях до курсового проекту наведені плоскі важільні механізми. Плоским механізмом називають механізм, усі ланки якого, рухаються в одній площині або в паралельних площинах [1].
У плоскому механізмі заздалегідь накладені загальні зв'язки позбавляють кожну з ланок трьох мір свободи, а саме: обертання навколо двох координатних осей, які лежать в площині руху механізму і ковзання уздовж осі, перпендикулярної до цієї площини. Тому кінематичні пари можуть накласти на відносний рух ланок, які утворюють кінематичну пару, або одну, або дві умови зв'язку. Таким чином, в плоскому механізмі можуть бути тільки наступні пари:
а) вищі кінематичні (наприклад, профілі зубчатих циліндрових коліс, що сполучаються, або система профіль кулачкової шайби - штовхач.) Число цих пар механізму позначатимемо
б) обертальна (шарнір) або поступальна (повзун) в тих парах, що направляють рух. Число таких пар механізму позначатимемо .
У завданнях на проект приведені механізми, в яких пасивні зв'язки відсутні. Тому, підрахувавши число ланок механізму та числа і кінематичних пар, можливо, за структурною формулою П. Л. Чебишева для плоского механізму, підрахувати його ступінь рухливості:
(1.1)
У приведеному записі означає тільки число всіх рухомих ланок механізму; стійка, отже, приведеною формулою не враховується. Точно також при підрахунку ступеню рухливості системи, що має в своєму складі кулачковий механізм, звичайно в число ланок не слід включати ролик. За цієї умови у всіх завданнях на проект матимемо W = 1, тобто положення механізму визначається завданням одного параметру, наприклад, кутової координати ланки, закон руху якої задається.
При підрахунку ступеня рухливості кулачкового механізму з урахуванням ролика одержуємо W = 2 - факт добре відомий і такий, що легко пояснюється теорією. Проте для спрощення завдання аналізу і синтезу механізмів не слід брати до уваги наявність ролика на першому етапі дослідження, оскільки він не міняє характер руху робочого органу (ланки, що виконує технологічний процес). Головним завданням ролика є заміна тертя ковзання, для якого коефіцієнт тертя досягає , на тертя кочення з коефіцієнтом , що на порядок нижче.
Для визначення ступеня рухливості просторового механізму використовується загальна формула Сомова – Малишева [1]:
, (1.2)
де - кількість кінематичних пар відповідного класу в механізмі.
1.2. Метод утворення плоских механізмів
У всіх завданнях на проект указано нерухому ланку (під штрихуванням) і безпосередньо пов'язану з нею, обертальною або поступальною парою, провідну ланку (стрілка показує напрям руху).
Сукупність вказаних двох ланок утворює так званий нульовий, або початковий, механізм (механізм l-го класу). Легко переконатися, що ця система володіє одним ступенем рухливості. Насправді, тут ; і тому за формулою (1.1) отримуємо:
Складніші схеми механізмів отримують послідовним приєднанням до початкового механізму (механізму l-го класу) ряду кінематичних ланцюгів. Для того, щоб новий складний механізм також мав одну ступінь рухливості, потрібно, щоб ці послідовні нашарування не змінювали ступінь рухливості початкового механізму. Це означає, що ступінь рухливості ланцюгів, які приєднуються, повинен дорівнювати нулю. Такі прості ланцюги, ступінь рухливості яких дорівнює нулю, називають нормальними ланцюгами, або групами Л. В. Ассура. Число ланок і число кінематичних пар у таких групах, як і способи їх побудови різні.
У завданнях зустрічаються тільки групи двох типів: двох - і чотирьох ланкові, які приєднуються вільними елементами кінематичних пар до механізму (або структурні видозміни цих двох типів).
Механізм, утворений нашаруванням одних тільки двох ланкових груп, називають механізмом 2-го класу; механізм, до складу якого входять і чотирьох ланкові групи, називають механізмом 3-го класу. Останні одержують з нормальних груп спрощенням їх структури, яке полягає в тому, що одну ланку з двома нижчими кінематичними парами замінюють однією вищою кінематичною парою. Така заміна не міняє ступені рухливості нормального ланцюга. Насправді, ланка з двома нижчими парами накладає на систему один зв'язок:
.
Вища кінематична пара також накладає один зв'язок і, отже, не тільки нормальний ланцюг, але і його видозміна володіє нульовим ступенем рухливості. Таким чином, з погляду структури двох ланкова група, що складається з двох ланок і трьох нижчих кінематичних пар, може бути замінена групою, що складається з однієї ланки, одного елементу вищої кінематичної пари і одного елементу нижчої пари. Чотирьох ланкова група, що складається з чотирьох ланок і шести нижчих кінематичних пар, може бути з погляду структури замінена ланцюгом, що складається з трьох ланок, чотирьох нижчих кінематичних пар і однієї вищої пари.
На рис. 1, зображена схема механізму двигуна з компресором, а на рис. 2 - відповідно його структурна схема.
Загалом, відмінність структурної схеми від кінематичної полягає в тому, що структурні видозміни замінені відповідними нормальними групами, в яких додаткові ланки позначені буквами замість цифр, а поступальні пари замінені умовно обертальними.
2. Методи кінематичного дослідження плоских механізмів
2.1. Завдання кінематичного дослідження плоских механізмів
Завдання кінематичного дослідження механізму полягає у визначенні:
1) положень ланок та точок механізму в різні моменти часу;
2) траєкторій деяких точок ланок;
3) величини і напрями лінійних швидкостей та прискорень точок, кутових швидкостей та прискорень ланок.
Для механізмів з одним ступенем рухливості задається закон руху однієї з ланок (як правило це головний вал машини). Цю ланку називають ведучою або провідною.
Визначення перерахованих кінематичних характеристик проводиться в межах одного періоду (циклу) сталого руху механізму для декількох положень, що дає можливість з достатнім наближенням вирішити поставлені завдання. Без знання згаданих кінематичних параметрів конструктор не зможе вирішувати подальшу задачу про раціональний підбір розмірів. Так, наприклад, траєкторії деяких точок механізму потрібні для визначення ходу ланок, контуру машин, а також для встановлення відповідності руху робочих ланок машини, правильної послідовності технологічного процесу.
У деяких машинах (у довбальних і стругальних верстатах) не допускаються великі зміни швидкості робочої ланки, оскільки від цього залежить стійкість ріжучого інструменту. Зі сказаного видно необхідність знання швидкостей точок деяких ланок і уміння для наочності зручно представляти їх у вигляді графіків.
За допомогою планів швидкостей визначають приведену масу (без знання якої не можливо визначити момент інерції маховика), закон руху машини і т. д.; плани прискорень потрібні для знаходження сил та моментів інерції ланок.
Кінематичне дослідження механізмів проводять із припущенням, що провідні ланки обертаються з постійною кутовою швидкістю, не дивлячись на те, що насправді кутова швидкість обертання кривошипа не є постійною і залежить від величини навантаження. Таке допущення робиться через невелику розбіжність між середньою і дійсною кутовою швидкістю кривошипу, крім того це технічно полегшує побудову планів прискорень і визначення величин прискорень ланок і точок механізму.
У посібнику розглядається побудова планів положень, швидкостей і прискорень механізмів II класу (за класифікацією І. І. Артоболевського).
2.2. Побудова положень ланок механізму
Для вирішення цього завдання повинні бути задані:
1) кінематична схема механізму;
2) закон руху провідної ланки.
Наприклад, потрібно
визначити положення механізму (кінематична
схема його зображена на рис. 18) через
рівні проміжки часу руху провідної
ланки
,
якщо задані координати нерухомих точок
,
,
і положення осі
тієї, що направляє повзун 6, розташованої
в площині креслення, а також довжини
ланок
,
,
і
.
Приймемо, що ведуча ланка (кривошип)
обертається з постійною кутовою швидкістю
.
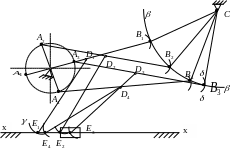
Рисунок 18. Механізм коливаючогося конвеєра
Провівши структурний аналіз механізму та побудувавши його структурну схему (рис. 19), встановлюємо, що цей механізм слід віднести до механізмів ІІ класу, оскільки до початкового механізму 1-2 приєднані дві двох повідкові групи: 3-4 і 5-6.
Рисунок 19. Структурна схема механізму коливаючогося конвеєра
По заданих
координатах визначаємо на кресленні
положення нерухомих точок
,
,
і осі
.
Затим проводимо коло радіусу
і відзначаємо на ній декілька положень:
(
,
,
...,
)
точки
провідної ланки, для яких потрібно
визначити положення всіх ланок механізму.
Положення решти ланок механізму,
відповідні заданим положенням ведучої
ланки
,
визначаємо методом засічок. Точка
рухається по дузі кола
радіусу
і завжди знаходиться на цій дузі. Її
положення
,
відповідне заданому положенню ланки
,
одержимо на перетині дуги
з дугою кола
радіусу
,
описаного з точки
.
З'єднавши точку
з точками
і
,
одержимо положення ланок 3 і 4 першої
структурної групи.
Для побудови
положення ланок 5-6 другої структурної
групи відзначимо на ланці
положення центру шарніра
.
Положення точки
,
що рухається по осі
,
одержимо на перетині осі
з дугою кола
радіусом
,
описаної з точки
.
З'єднавши крапку
з точкою
одержимо положення ланки
і повзуна
,
які складають другу приєднану групу
ланок.
При викреслюванні положень механізму потрібно вказати числовий масштаб креслення. Під масштабом розуміють число, що показує, скільки одиниць деякої величини зображає один міліметр креслення.
Умовимося дійсні
довжини ланок позначати буквою
з індексами назви ланки, тобто
,
,
і т. д., а довжини цих же ланок, відкладені
на схемі в масштабі, через
,
,
і т. д.
Тоді, очевидно, масштаб креслення можливо виразити, поділивши дійсну величину на довжину відрізка в міліметрах, що зображає цю величину на кресленні, тобто:
.
(2.1)
Надалі всі масштаби
позначатимемо буквою
з індексом величини, що зображується
на кресленні, наприклад:
- масштаб довжини,
- масштаб плану швидкостей,
-
масштаб плану прискорень. Відповідно
розмірності цих масштабів будуть:
;
;
.
2.3. Побудова траєкторій окремих точок механізму і визначення крайніх положень вихідної ланки
Побудову траєкторії точки ланки механізму проводять в такій послідовності:
1) викреслюють механізм в декількох положеннях в межах одного циклу його роботи;
2) у кожному з накреслених положень механізму відзначають положення точки, траєкторія якої повинна бути побудована;
3) знайдені положення точки сполучають послідовно між собою плавної кривої.
На рис. 20 приведений
приклад побудови траєкторії точки
,
що належить шатуну
механізму
,
який складається з чотирьох ланок.
Задавшись рядом положень точки
(
,
,…..
)
на колі
,
визначаємо відповідні положення точки
(
,
,
,…
).
Положення точки
визначаємо (рис. 20) роблячи засічки на
прямих
,
,
...,
дугами радіусу
з точок
,
,
...,
.
З'єднавши послідовно одержані точки
,
,
...,
плавною кривою, одержимо траєкторію
точки
за один оберт кривошипу.
Рисунок 20. Побудова траєкторії точки , що належить шатуну механізму
В деяких випадках
траєкторією точки є дуга кривої, по якій
вона рухається спочатку в одному, а
потім у зворотному напрямі. Відстань
між крайніми положеннями точки на її
траєкторії в цьому випадку називають
ходом точки. На рис. 18, траєкторією точки
є дуга кола радіусу
,
а на рис. 3 – відрізок прямої
.
Крайні положення
і
точки
відповідають тим положенням механізму,
при яких шатун
і кривошип
лежать на одній прямій; ці крайні
положення можна визначити, роблячи
засічки на траєкторії точки
з центру обертання кривошипа дугами
радіусів (
+
)
і (
-
).
В більшості випадків буває корисно за
початкове (нульове) положення механізму
вибирати те його положення, в якому
відома ланка займає одне з крайніх
положень.
Аналогічно визначають траєкторію точки ланки і в більш складніших випадках.
2.4. Побудова кінематичних діаграм
Кінематичний аналіз механізмів можливо здійснювати різними методами. Найбільш поширеними є три методи кінематичного аналізу: аналітичний, графоаналітичні, експериментальний.
В окремих випадках, коли виникає необхідність вивчити кінематику окремої точки механізму, перевагу віддають методу кінематичних діаграм.
Кінематична
діаграма є графічним зображенням зміни
одного з кінематичних параметрів
(переміщення, швидкості або прискорення)
точки або ланки досліджуваного механізму
у функції часу, кута повороту або
переміщення провідної ланки цього
механізму
,
,
,
або
,
,
.
Вони можуть бути одержані в результаті експериментальних досліджень або графічних побудов при розв'язанні задач на визначення положень точок та ланок механізму.
Як приклад, побудуємо
кінематичну діаграму зміни відстані
точки
повзуна механізму стругального верстату
(рис. 21), починаючи від її лівого крайнього
положення
,
за один повний оборот кривошипу
(за один цикл роботи механізму).
Кривошип
обертається з постійною кутовою
швидкістю, яка дорівноює
оборотів на хвилину.
При рівномірному обертанні кривошипу,
точка
за рівні проміжки
часу проходить рівні відрізки шляху.
Для побудови графіка
траєкторію
точки
ділять, в залежності від потрібної
точності, на декілька
рівних частин (у наведеному прикладі
траєкторія
точки
поділена на 8 рівних
частин) і позначають відповідні положення
точки
(рис. 21).
Розмітку
(нумерацію) траєкторії точки
починають із положення кривошипа
при якому досліджувана точка повзуна
буде в крайньому, правому
чи лівому положеннях ("мертвому"
положенні механізму). Це положення
кривошипа вважають початковим і нумерують
його цифрою
.
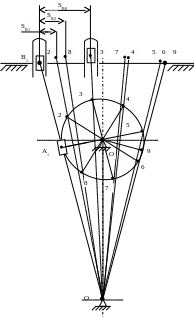
Рисунок 21. Плани механізму стругального верстата
Побудова діаграми здійснюється в наступному порядку:
1) викреслюємо план
механізму в масштабі
у декількох, наприклад, дванадцяти
положеннях, відповідних послідовним
поворотам кривошипа
на кут 300
або восьми положеннях (рис. 21), відповідних
послідовним поворотам кривошипа
на кут 450.
За початкове положення кривошипа
приймаємо
,
при якому повзун
займає крайнє ліве положення
.
Дев’яте положення визначається як
кінець прямого ходу повзуна
;
2) будуємо осі
координат
-
(рис. 22) і на осі абсцис (
)
відкладаємо відрізок
в мм, що зображає час одного повного
обороту кривошипу в масштабі
.
Тоді
,
(2.2)
де
- час одного обороту кривошипа, с.;
- масштаб часу;
.
(2.3)
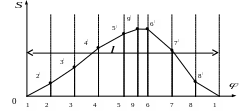
Рисунок 22. Діаграма переміщень точки вихідної ланки в залежності від кута повороту кривошипа
Відрізок
ділимо на 8 рівних частин і у відповідних
точках 1,2,3... по осі ординат відкладаємо
відстані
,
,
,
...,
,
пройдені точкою
від її крайнього лівого положення
.
До крайнього
правого положення
відстань повзуна
від початкового
зростає, а починаючи з положення
,
вона зменшуватиметься; коли кривошип
прийде в початкове положення
,
ордината кривої (
-
)
буде дорівнювати нулю;
3) з’єднуємо
послідовно плавною кривою одержані
точки
,
,
,
,
... . Одержана крива і буде діаграмою
відстаней точки
від початкового положення (рис. 22).
Якщо величини
відстані
,
,
,
...,
відкладати прямо зі схеми (рис. 21), то
масштаб
діаграми (
-
)
буде дорівнювати масштабу
;
якщо ж ці відстані доводиться зменшити
у
разів, то величину
відповідно збільшують у
разів, тобто:
.
(2.4)
При рівномірному
обертанні кривошипа можливо вважати,
що по осі абсцис відкладено не час
,
а шлях
точки
,
при цьому масштаб по осі абсцис:
,
(2.5)
де значення повинне бути взяте з креслення, мм.
Якщо ж по осі абсцис
відкладати кути повороту кривошипа
,
відлічуючи їх по ходу годинникової
стрілки від початкового положення
,
то дана діаграма відображає функціональну
залежність
і масштаб по осі абсцис
(2.6)
2.5.
Побудова діаграм швидкостей (
-
)
і прискорень (
-
)
методом графічного диференціювання
Для побудови діаграм швидкостей і прискорень потрібно спочатку побудувати діаграму переміщень ( - ). На рис. 23А побудована довільна діаграма ( - ), не пов’язана ні з однією кінематичною схемою, що наведені в посібнику.
Для побудови
діаграми швидкості (
-
)
поступаємо таким чином:
1) під діаграмою
переміщень (
-
)
(рис. 23А) будуємо осі координат
,
(рис. 23Б) і на продовженні осі
вліво відкладаємо відрізок
мм, отримуємо точку
- полюс;
2) з точки
проводимо промені
;
;
,
...
паралельно хордам кривої (
-
)
на ділянках
;
;
...
Ці промені відсічуть на осі
відрізки
;
;
..., пропорційні середній швидкості
на відповідній ділянці діаграми;
3) відкладемо ці відрізки на середніх ординатах відповідних ділянок;
4) з'єднаємо ряд
одержаних точок
;
;
;
... плавною кривою; ця крива буде діаграмою
швидкості (
-
).
Слід мати на увазі, що ділянки, на яких крива має екстремум (як, наприклад, ділянка 6-7 на рис. 23А, і 10-11 на рис. 23Б), слід розділити додатково на дві ділянки кожну, впродовж яких крива не має екстремуму (найбільшої або найменшої величини).
Маючи діаграму
швидкостей (
-
),
аналогічно будуємо діаграму тангенціальних
прискорень (
-
),
представлену на рисунку 23В.
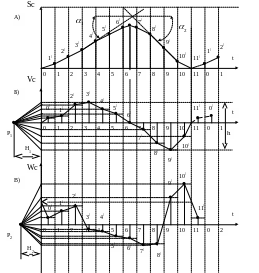
Рисунок 23. Кінематичні діаграми переміщень ( - ), швидкостей ( - ) і прискорень ( - )
При побудові діаграм ( - ) і ( - ) описаним методом не можна одержати ті ділянки цих діаграм, які відповідають половині крайніх ділянок осі абсцис. Щоб закінчити побудову діаграм, потрібно додатково побудувати середні значення і для однієї - двох ділянок наступного циклу. З'єднавши плавною кривою точки, відповідні останнім ділянкам першого циклу і першим ділянкам наступного циклу, відсічемо на крайній правій осі ординат відрізок, який слід відкласти на крайній лівій осі ординат циклу. Після цього остаточно добудовуємо всю криву, як це вказано на рисунку 44 штриховими лініями.
Масштаб
діаграм (
-
)
і (
-
)
залишається таким же, як і раніше, а
масштаби
по осях ординат визначаються по формулах:
для діаграми швидкостей
,
(
)
(2.7)
для діаграми прискорення:
,
(
)
(2.8)
де
і
- відрізки, узяті з креслення, мм.
Якщо по осі абсцис
відкладено не час
,
а кут повороту кривошипа
,
то у формулах (2.5)
і (2.6)
потрібно поставити замість
величину
.
Тоді одержимо:
,
(
)
(2.9)
і
,
(
)
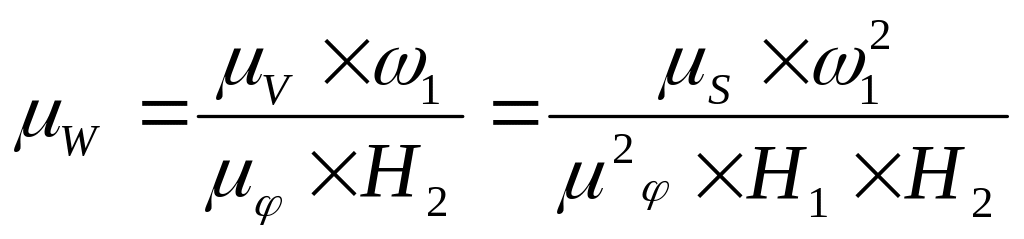(2.10)
де:
,
(
).
З формул (2.9) і (2.10) видно, що величини масштабу диференціальних кривих залежать від відповідної полюсної відстані, і , яку вибирають так, щоб диференціальна крива помістилася на відведеному для неї місці креслення.
Тому слід визначати [4] за формулою:
(2.11)
де -
і
- найбільші кути нахилу хорд (або дотичних)
на висхідній і низхідній ділянках
інтегральної кривої (
-
);
визначення їх величини вказане на
рисунок 20.
- висота діаграми
-
,
що буде побудована.
Відстань між осями
абсцис
діаграм
(
-
)
і (
-
)
повинна
бути:
.
(2.12)
Аналогічним
способом визначають необхідну висоту
майданчика для діаграми (
-
)
і відстань
між осями абсцис.
2.6. Відповідності між діаграмами переміщень, швидкостей і дотичних прискорень
Між інтегральною і диференціальною кривими є певні характерні залежності, які потрібно враховувати, контролюючи точність побудови діаграм:
1. Екстремальним значенням ординат інтегральної кривої відповідають нульові значення ординат диференціальної кривої.
2. Точкам перегину інтегральної кривої відповідають екстремальні значення ординат диференціальної кривої.
3. Зростаючим ординатам інтегральної кривої відповідають позитивні значення ординат диференціальної кривої, а що убуває - негативні.
4. Ординати диференціальної кривої, відповідні початку і кінцю періоду сталого руху, рівні між собою.
5. Дотичні, проведені до диференціальної кривої в крапках, відповідних початку і кінцю періоду сталого руху, мають один і той же напрямок (паралельні одна до одної).
2.7. Кінематичний аналіз графоаналітичним методом
Побудова планів швидкостей та прискорень точок та ланок механізму починаємо від вхідної ланки, закон руху якої задано. Послідовно переходячи від механізму 1го класу до груп ланок, приєднаних до механізму 1-го класу, визначаються швидкості та прискорення всіх характерних точок і ланок механізму.
2.7.1. Кінематичний аналіз ведучої ланки
Для механізмів,
які розглядаються в курсових проектах,
ведучою ланкою є кривошип (рисунок 24).
Кінематичний аналіз здійснюється за
припущенням, що кривошип обертається
з постійною кутовою швидкістю
,
а отже кутове прискорення
.
Рисунок 24 Механізм 1го класу
Швидкість точки , яка належить кривошипу 2 знаходимо з рівняння:
.
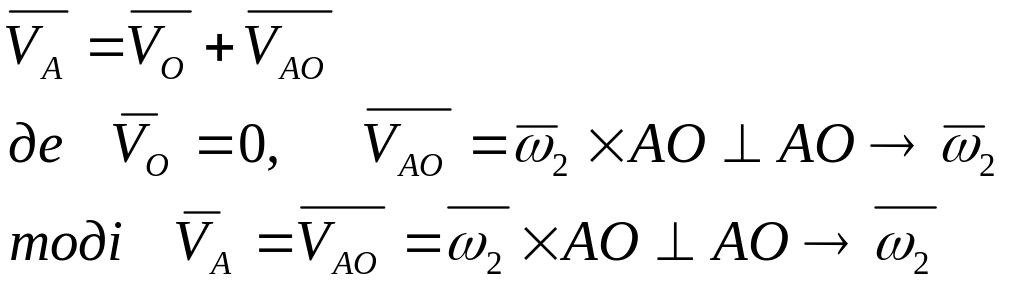(2.13)
Прискорення точки , яка належить кривошипу 2 знаходимо з рівняння:
,
(2.14)
Нормальна складова прискорення точки відносно центру обертання вираховується за формулою:
.
(2.15)
Тангенціальна складова прискорення точки відносно центру обертання вираховується за формулою:
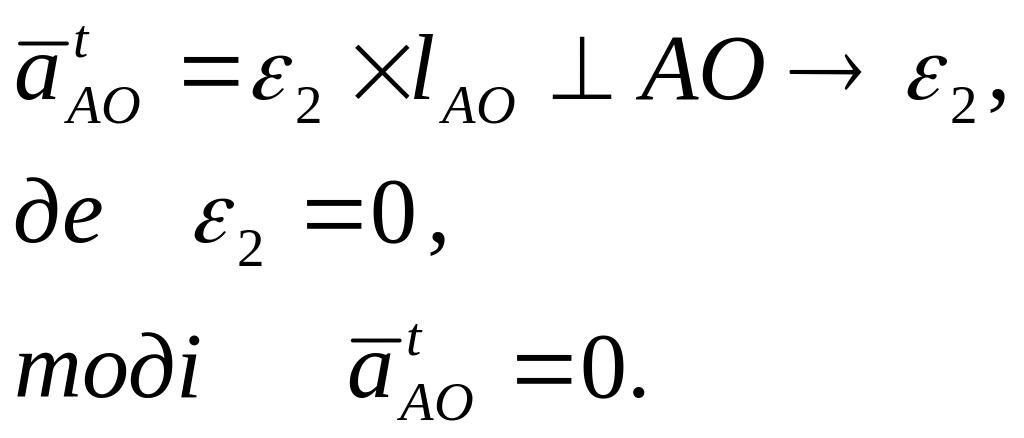(2.16)
Таким чином:
.
(2.17)
При побудові планів швидкостей та прискорень слід дотримуватися правил:
1). Побудувати кінематичну схему механізму в масштабі (приклад на рис. 25);
Рисунок 25 Кривошипо-кулісний механізм
2). Виконати структурний аналіз механізму, побудувати структурну схему (рис. 25);
3). Побудувати плани швидкостей та прискорень.
а). Побудову планів швидкостей та прискорень вести послідовно за структурними групами, в тому порядку, в якому вони приєднуються до основного механізму. Спочатку розглядається механізм 1го класу, затим – перша, приєднана до нього структурна група, потім друга структурна група і т.д.;
б). У структурній групі спочатку необхідно визначити швидкості та прискорення крайніх точок групи, якими вона приєднується до ланок інших груп. Після цього визначаються швидкості та прискорення точок внутрішніх кінематичних пар і тільки потім - швидкості та прискорення інших характерних точок ланок, які входять у групу;
в). Для визначення
швидкості точки внутрішньої кінематичної
пари групи ІI-го
класу складається система з двох
векторних рівнянь. У першому рівнянні
швидкість точки
внутрішньої кінематичної пари визначається
через відому швидкість точки першої
ланки, а в другому - через відому швидкість
точки другої ланки. Для механізму,
зображеному на рисунку , така система
має вигляд:
.
(2.18)
Систему векторних
рівнянь вирішують графічним методом,
шляхом побудови плану швидкостей. Для
цього спочатку вибирається довільна
точка – полюс
,
всі швидкості в якій дорівнюють нулю.
Від полюса відкладається перший вектор
швидкості
з першого рівняння системи (2.18) прямою
лінією довільної довжини, проведеною
перпендикулярно ланці
у напрямку кутової швидкості
.
Таким чином, на плані швидкостей вектор
- зображується лінією початок якої полюс
,
а кінець – точка
і її довжина
.
Величина швидкості
визначається за формулою (2.13).
Визначивши величину вектора
,
а також його довжину в міліметрах на
плані швидкостей, визначають масштаб
плану за формулою:
,
(2.19)
де
- величина швидкості точки
,
;
- довжина вектора в міліметрах на плані швидкостей.
До вектора
потрібно долучити вектор
.
Про нього відомо тільки напрямок –
точка
,
яка належить ланці 3, рухається відносно
точки
,
яка належить ланці 4, паралельно кулісі
.
Тому, через точку
,
кінець вектора
,
проводимо лінію дії вектора
паралельно
.
Друге рівняння
системи починаємо креслити з полюса
.
Швидкість
точки
дорівнює нулю, так як точка
- нерухома точка. На плані швидкостей з
полюса
відкладаємо відрізок нульової довжини.
Таким чином і початок вектора
і його кінець – точка
знаходиться в полюсі
.
До вектора швидкості
додається вектор
.
Про нього відомо тільки напрямок –
точка
,
яка належить ланці 4, рухається відносно
точки
,
яка належить ланці 4, перпендикулярно
кулісі
.
Тому, через точку
,
кінець вектора
,
проводимо лінію дії вектора
перпендикулярно кулісі
.
Лінії дії векторів
і
перетинаються в точці
(рис. ). Відрізок
на плані швидкостей зображує в масштабі
вектор
,
а відрізок
на плані швидкостей зображує в масштабі
вектор
.
Величина швидкості
визначається як:
,
аналогічно
.
Вектор швидкості
це відрізок
,
на плані швидкостей (рис. 25) він співпадає
з відрізком
і тому швидкості
,
що відповідає другому рівняння системи
(2.18).
Для визначення ланок механізму з точки зору їх швидкостей необхідно для кожної ланки визначити лінійні швидкості не менше двох точок та власну кутову швидкість ланки.
Для ланки 3 визначено
швидкість точки
,
ланка 3 це повзун, а для повзуна швидкості
всіх точок однакові, власна кутова
швидкість повзуна дорівнює нулю
.
Таким чином для ланки 3 визначено лінійні
швидкості не менше двох точок та власна
кутова швидкість ланки.
Для ланки 4 визначено швидкість та , кутова швидкість визначається за формулою:
,
а напрямок
співпадає з напрямком вектора швидкості
.
Таким чином для ланки 4 визначено лінійні
швидкості двох точок та власна кутова
швидкість ланки.
6). Для визначення прискорення точки внутрішньої кінематичної пари групи ІI-го класу складається система з двох векторних рівнянь. У першому рівнянні прискорення точки внутрішньої кінематичної пари визначається через відоме прискорення точки першої ланки, а в другому - через відоме прискорення точки другої ланки. Для механізму, зображеному на рисунку , така система має вигляд:
(2.20)
Систему векторних
рівнянь вирішують графічним методом,
шляхом побудови плану прискорень. Для
цього спочатку вибирається довільна
точка – полюс
,
всі прискорення в якій дорівнюють нулю.
Від полюса відкладається перший вектор
прискорення
з першого рівняння системи (3.20) прямою
лінією довільної довжини, проведеною
паралельно ланці
у напрямку від точки
до точки
згідно рівняння (2.15).
Таким чином, на плані прискорень вектор
- зображується лінією початок якої полюс
,
а кінець – точка
і його довжина
.
Величина прискорення
визначається за формулою (2.17).
Визначивши величину вектора
,
а також його довжину в міліметрах на
плані прискорень, визначають масштаб
плану за формулою:
,
де
- величина прискорення точки
,
;
- довжина вектора в міліметрах на плані прискорень.
До вектора
потрібно долучити вектор
.
Коріолісова складова відносного
прискорення визначається за формулою:
.
(2.21)
Всі складові формули попередньо визначені і величина вираховується. Для визначення напрямку потрібно відносну швидкість прикласти до ланок 3 та 4 і повернути разом з ланками на кут у 900 відносно центру обертання (точка ) в напрямку кутової швидкості . Тоді напрямок буде співпадати з напрямком повернутої швидкості (рис. 26).
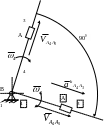
Рисунок 26. Визначення напрямку Коріолісової складової відносного прискорення
На плані прискорень
вектор
відкладається відрізком який вираховується
за формулою
.
До кінця вектора
додається лінія дії вектора
– перпендикулярно до вектора
,
або (що одне й теж) паралельно вектору
швидкості
.
Друге рівняння
системи починаємо креслити з полюса
.
Прискорення
точки
дорівнює нулю, тому що точка
- нерухома точка. На плані прискорень з
полюса
відкладаємо відрізок нульової довжини.
Таким чином і початок вектора
і його кінець – точка
знаходиться в полюсі
.
До вектора прискорення
додається вектор
.
Величина нормальної складової відносного прискорення вираховується за формулою:
.
Всі складові
формули попередньо визначені і величина
вектора
вираховується. На плані прискорень
вектор
відкладається відрізком з урахуванням
масштабу:
.
Напрямок нормальної складової
відносного прискорення – паралельно
ланці
від точки
до точки
.
До кінця вектора
на плані прискорень додається лінія
дії вектора
– перпендикулярно до вектора
,
або (що одне й теж) перпендикулярно
кулісі
.
Лінії дії векторів
і
перетинаються в точці
(рис. 25). Відрізок
на плані прискорень зображує в масштабі
вектор
,
а відрізок
на плані зображує в масштабі
вектор
.
Дійсна величина прискорень
,
,
,
,
визначається шляхом множення величини
відповідного відрізку на плані прискорень
на масштаб
плану прискорень.
Для визначення ланок механізму з точки зору їх прискорень необхідно для кожної ланки визначити лінійні прискорення не менше двох точок та власне кутове прискорення ланки.
Для ланки 3 визначено
прискорення точки
,
ланка 3 це повзун, а для повзуна прискорення
всіх точок однакові, власне кутове
прискорення повзуна дорівнює нулю
.
Таким чином для ланки 3 визначено лінійні
прискорення не менше двох точок та
власне кутове прискорення ланки.
Для ланки 4 визначено
прискорення
та
,
кутове прискорення визначається за
формулою:
,
напрямок
співпадає з напрямком вектора прискорення
.
Таким чином для ланки 4 визначено лінійні
прискорення двох точок та власне кутове
прискорення ланки.
г). Визначаються швидкості та прискорення характерних точок ланок механізму. До характерних точок ланок найчастіше відносяться центри маси ланок та кінематичні пари, якими до ланки приєднується наступна група з нульовим ступенем рухомості.
Швидкості та
прискорення характерних точок ланок
механізму, маючи плани швидкостей та
прискорень, доцільно визначати за
теоремою подібності. Для механізму,
зображеному на рису. 25 характерними
точками є точка центру маси
куліси та
точка
.
Швидкість точки , на плані швидкостей знаходиться за теоремою подібності, із пропорції:
,
звідки:
.
Величина швидкості точки обчислюється за формулою:
.
Швидкість точки
,
знаходиться на плані швидкостей за
теоремою подібності: на відрізку
будується трикутник
,
подібний до трикутника
плану механізму. Відрізок
- вектор швидкості
на плані швидкостей. Величина швидкості
точки
обчислюється за формулою:
.
Аналогічно ці ж точки знаходяться на плані прискорень. Тоді величина прискорення точки обчислюється за формулою:
,
а величина прискорення точки за формулою:
Приклад. Кінематичний аналіз кривошипо - повзунного механізму графоаналітичним методом.
Кінематична схема (план механізму) наведено на рис. 27. Згідно з розділом 1.4 проводиться структурний аналіз механізму та будується структурна схема (рис. 27).
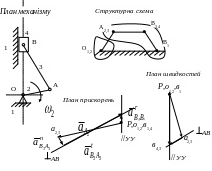
Рисунок 27. Кривошипо-повзунний механізм
Швидкість точки знаходиться згідно з формулою (2.13):
.
Для визначення
швидкості точки внутрішньої кінематичної
пари групи ІI-го
класу складається система з двох
векторних рівнянь. У першому рівнянні
швидкість точки
внутрішньої кінематичної пари визначається
через відому швидкість точки
першої
ланки, а в другому
- через відому швидкість точки
.
Для механізму, зображеному на рис. 27 ,
така система має вигляд:
.
(3.22)
Систему векторних рівнянь вирішують графічним методом, побудувавши план швидкостей (рис. 27). Для цього спочатку вибирається довільна точка – полюс , всі швидкості в якій дорівнюють нулю. Від полюса відкладається перший вектор швидкості з першого рівняння системи (2.22) прямою лінією довільної довжини, проведеною перпендикулярно ланці у напрямку кутової швидкості . Таким чином, на плані швидкостей вектор - зображується лінією початок якої полюс , а кінець – точка і її довжина . Величина швидкості визначається за формулою (2.13). Визначивши величину вектора , а також його довжину в міліметрах на плані швидкостей, визначають масштаб плану за формулою:
,
де - величина швидкості точки , ;
- довжина вектора в міліметрах на плані швидкостей.
До вектора
потрібно долучити вектор
.
Про нього відомо тільки напрямок –
точка
,
яка належить ланці 3, рухається відносно
точки
,
яка належить ланці 3, перпендикулярно
шатуну
.
Тому, через точку
,
кінець вектора
,
проводимо лінію дії вектора
перпендикулярно
.
Друге рівняння
системи починаємо креслити з полюса
.
Швидкість
точки
,
що належить ланці 1, дорівнює нулю, так
як ланка 1 нерухома. На плані швидкостей
з полюса
відкладаємо відрізок нульової довжини.
Таким чином і початок вектора
і його кінець – точка
знаходиться в полюсі
.
До вектора швидкості
додається вектор
.
Про нього відомо тільки напрямок –
точка
,
яка належить ланці 4, рухається відносно
точки
,
яка належить ланці 1, паралельно
направляючій
.
Тому, через точку
,
кінець вектора
,
проводимо лінію дії вектора
паралельно
.
Лінії дії векторів
і
перетинаються в точці
(рис. 27). Відрізок
на плані швидкостей зображує в масштабі
вектор
,
а відрізок
на плані швидкостей зображує в масштабі
вектор
.
Величина швидкості
визначається як:
,
аналогічно
.
Вектор швидкості
це відрізок
,
на плані швидкостей (рис. 27) він співпадає
з відрізком
і тому швидкості
,
що відповідає другому рівнянню системи
(2.22).
Для визначення ланок механізму, з точки зору їх швидкостей, необхідно для кожної ланки визначити лінійні швидкості не менше як двох точок та власну кутову швидкість ланки.
Для ланки 3 визначено
швидкість точки
-
та точки
-
,
крім того відносна швидкість цих точок
-
,
кутова швидкість визначається за
формулою:
,
напрямок
співпадає з напрямком вектора швидкості
.
Таким чином для ланки 3 визначено лінійні
швидкості двох точок та власна кутова
швидкість ланки.
Для ланки 4 визначено
швидкість точки
,
ланка 4 це повзун, а для повзуна швидкості
всіх точок однакові, власна кутова
швидкість повзуна дорівнює нулю
.
Таким чином для ланки 4 визначено лінійні
швидкості не менше двох точок та власна
кутова швидкість ланки.
Прискорення точки , яка належить кривошипу 2 знаходимо з рівняння:
,
Нормальна складова прискорення точки відносно центру обертання вираховується за формулою:
.
Тангенціальна складова прискорення точки відносно центру обертання вираховується за формулою:
Таким чином:
.
Для визначення прискорення точки внутрішньої кінематичної пари групи ІI-го класу складається система з двох векторних рівнянь. У першому рівнянні прискорення точки внутрішньої кінематичної пари визначається через відоме прискорення точки першої ланки, а в другому - через відоме прискорення точки другої ланки. Для механізму, зображеному на рисунку 27, така система має вигляд:
(2.23)
Систему векторних рівнянь вирішують графічним методом, шляхом побудови плану прискорень. Для цього спочатку вибирається довільна точка – полюс , всі прискорення в якій дорівнюють нулю. Від полюса відкладається перший вектор прискорення з першого рівняння системи (3.23) прямою лінією довільної довжини, проведеною паралельно ланці у напрямку від точки до точки згідно рівняння (2.15). Таким чином, на плані прискорень вектор - зображується лінією початок якої полюс , а кінець – точка і його довжина . Величина прискорення визначається за формулою (3.17). Визначивши величину вектора , а також його довжину в міліметрах на плані прискорень, визначають масштаб плану за формулою:
,
де - величина прискорення точки , ;
- довжина вектора в міліметрах на плані прискорень.
До вектора
потрібно долучити вектор
.
Нормальна складова відносного прискорення
визначається за формулою:
.
Всі складові формули попередньо визначені і величина вираховується.
Друге рівняння
системи починаємо креслити з полюса
.
Прискорення
точки
дорівнює нулю, тому що точка
- нерухома точка. На плані прискорень з
полюса
відкладаємо відрізок нульової довжини.
Таким чином і початок вектора
і його кінець – точка
знаходиться в полюсі
.
До вектора прискорення
додається вектор
.
Коріолісова складова відносного прискорення визначається за формулою:
.
Так як
,
то
.
На плані прискорень
вектор
відкладається в полюсі
(точці
).
До кінця вектора
додається лінія дії вектора
– перпендикулярно до вектора
,
або (що одне й теж) паралельно вектору
швидкості
,
тобто паралельно лінії
(
).
Лінії дії векторів
і
перетинаються в точці
(рис. 27). Відрізок
на плані прискорень зображує в масштабі
вектор
,
а відрізок
на плані зображує в масштабі
вектор
.
Дійсна величина прискорень
,
,
,
,
визначається шляхом множення величини
відповідного відрізку на плані прискорень
на масштаб
плану прискорень.
Для визначення ланок механізму, з точки зору їх прискорень, необхідно для кожної ланки визначити лінійні прискорення не менше двох точок та власне кутове прискорення ланки.
Для ланки 3 визначено
прискорення
та
,
кутове прискорення
визначається за формулою:
,
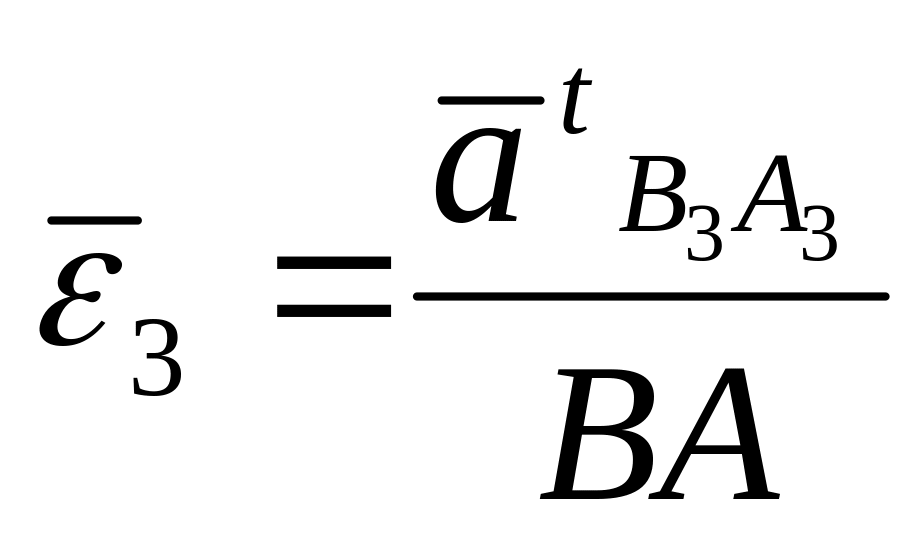напрямок співпадає з напрямком вектора прискорення . Таким чином для ланки 3 визначено лінійні прискорення двох точок та власне кутове прискорення ланки.
Для ланки 4 визначено
прискорення
точки
,
ланка 4 це повзун, а для повзуна прискорення
всіх точок однакові, власне кутове
прискорення повзуна дорівнює нулю
.
Таким чином для ланки 4 визначено лінійні
прискорення не менше двох точок та
власне кутове прискорення ланки.
г). Визначаються швидкості та прискорення характерних точок ланок механізму. До характерних точок ланок найчастіше відносяться центри маси ланок та кінематичні пари, якими до ланки приєднується наступна група з нульовим ступенем рухомості.
Швидкості та
прискорення характерних точок ланок
механізму, маючи плани швидкостей та
прискорень, доцільно визначати за
теоремою подібності. Для механізму,
зображеному на рис. 27 характерною точкою
є точка центру маси
куліси
шатуна
.
Швидкість точки , на плані швидкостей знаходиться за теоремою подібності, із пропорції:
,
звідки:
.
Величина швидкості точки обчислюється за формулою:
.
Аналогічно ці ж точки знаходяться на плані прискорень. Тоді величина прискорення точки обчислюється за формулою:
.