Тема 5. Розмірні ланцюги

План

1. Види та призначення розмірних ланцюгів.

2. Методи досягнення точності замикаючої ланки.

3. Розрахунок розмірних ланцюгів на максимум – мінімум.

4. Особливості розрахунку площинних не лінійних та просторових розмірних ланцюгів

5. Використання розмірного аналізу при ремонті машин.

1.) Види та призначення розмірних ланцюгів.

Машини і прилади, які збираються із окремих деталей, добре працюють тільки в тому випадку, коли кожна деталь буде займати задане їй місце відносно інших деталей. В реальних машинах і механізмах, взаємне розташування осей і поверхонь окремих деталей залежить, як правило, від багатьох складових розмірів. Розрахунок допусків на всі ці розміри вирішується за допомогою розмірного аналізу.

Встановлення раціональних допусків розмірів, які визначають взаємне положення осей і поверхонь окремих деталей по-перше забезпечує взаємозамінність і полегшує процес зборки, а по-друге в значній мірі визначає експлуатаційні якості машини.

Велике значення має використання розмірного аналізу в процесі ремонту машин, коли потрібно повертати первинне положення осей і поверхонь.

Розмірний аналіз базується на побудові і розрахунку розмірних ланцюгів. Нормативними документами для його проведення є стандарти ГОСТ 16319, який встановлює термінологію та ГОСТ 16320 – методи розрахунку.

Розмірним ланцюгом називається сукупність розмірів, які утворюють замкнутий контур і безпосередньо приймають участь у вирішенні задачі по визначенню взаємного положення осей і поверхонь деталі, механізму або машини в цілому.

Розміри, які утворюють розмірний ланцюг, називають розмірними ланками. Ланка, яка в процесі зборки або виготовлення деталі виявляється останньою називається замикаючою. Інші ланки називають складовими. Прийнято умовно позначати складові ланки одного ланцюга однією буквою алфавіту з різними чисельними індексами.

В залежності від задач, що вирішуються, розрізняють конструкторські, технологічні, ремонтні та вимірювальні розмірні ланцюги. Задачею конструкторського розмірного ланцюга є забезпечення необхідної точності при конструюванні деталей та збірних одиниць. Аналогічно, для технологічних, ремонтних та вимірювальних розмірних ланцюгів, задачами є забезпечення необхідної точності в процесі виготовлення, ремонту, вимірювання деталей та збірних одиниць.

Розмірні ланцюги поділяють на подетальні та збірні.

Рисунок 5.1. - Подетальний, плоский лінійний розмірний ланцюг валу

Розміри ланок ланцюга також називають розмірними ланками і для зручності розрахунків реальний ланцюг замінюють його схемою. Схема подетального плоского лінійного розмірного ланцюга валу (рис. 5.1) наведена на (рис 5.2).

Рисунок 5.2 - Схема подетального лінійного розмірного ланцюга валу

Складові ланки ланцюга по-різному впливають на замикаючу ланку. У випадку, коли зі збільшенням розміру складової ланки збільшується і розмір замикаючої ланки, то така складова має назву збільшуючої. У випадку, коли зі збільшенням розміру складової ланки зменшується розмір замикаючої ланки, то така складова має назву зменшуючої.

На рисунку 5.2 замикаючою ланкою є розмір (він обробляється останнім при виготовленні деталі), збільшуючою ланкою є розмір , а зменшуючими ланками – розміри і .

На рисунку 4.3 наведено зборочне креслення, а на рисунку 5.4 - схема збірного плоского лінійного розмірного ланцюга. Замикаючою ланкою тут є розмір , який отримують у результаті зборки вузла.

Рисунок 5.3 - Збірний, плоский лінійний розмірний ланцюг

По розташуванню ланок ланцюги можуть бути: плоскими (всі ланки розташовані в одній або паралельних площинах); просторовими (ланки розташовані в не паралельних площинах). Крім того плоскі і просторові ланцюги можуть бути: лінійними (ланки паралельні); кутовими (всі ланки кутові величини);змішаними (ланки мають кутові і лінійні величини). Найбільш розповсюдженими є плоскі лінійні розмірні ланцюги.

Головна властивість розмірного ланцюга – це його замкненість розмірного контуру і вплив на будь-яку ланку ланцюга відхилень інших ланок.

Рисунок 5.4 - Схема збірного плоского лінійного розмірного ланцюга

Побудова розмірного ланцюга починається з виявлення замикаючої ланки (розміру, до точності якого встановлюються певні технічні вимоги, так як він визначає якість роботи даного збірного вузла або деталі). Після цього виявляються збільшуючі та зменшуючі розміри і будується схема розмірного ланцюга.

Для побудови схеми розмірного ланцюга (рис. ) у верхній її частині відкладаються розміри всіх збільшуючих ланок, а в нижній частині – зменшуючих та замикаючої ланки.

Так як розмірний ланцюг – це замкнутий контур, то сума розмірів збільшуючих ланок повинна дорівнювати сумі розмірів зменшуючих ланок разом із замикаючою ланкою:

,

звідки:

,

де - номінальний розмір замикаючої ланки;

- сума номінальних розмірів збільшуючих ланок;

- сума номінальних розмірів зменшуючих ланок;

- число збільшуючих ланок;

- загальне число ланок ланцюга.

Для універсалізації рівняння розмірного ланцюга (щоб воно було придатним для розрахунків будь-якого розмірного ланцюга) вводиться поняття „передаточного відношення”:

.

Для лінійного ланцюга передаточне відношення дорівнює:

для збільшуючих ланок ;

для зменшуючих ланок .

Тоді для будь-якого виду розмірних ланцюгів:

.

2.) Методи досягнення точності замикаючої ланки

В процесі конструювання при розрахунках розмірних ланцюгів вирішуються пряма та зворотна задачі.

Прямою задачею розрахунку розмірних ланцюгів є визначення допусків та межових відхилень на всі складові ланки по заданому допуску та межовим відхиленням замикаючої ланки.

Зворотна задача розрахунку розмірних ланцюгів полягає у визначенні допусків та межових відхилень замикаючої ланки по заданим допускам та межовим відхиленням всіх складових ланок. Як правило, зворотна задача використовується для перевірки правильності призначення допусків та межових відхилень складових ланок.

Обидві ці задачі мають на меті досягнення необхідної точності замикаючої ланки і можуть вирішуватися різними методами, які можливо поділити на дві групи.

1 – група – методи, які забезпечують взаємозамінність у подетальних та збірних розмірних ланцюгах:

- метод повної взаємозамінності, який забезпечується розрахунком на максимум-мінімум;

- метод не повної взаємозамінності, який забезпечується розрахунком за допомогою методів теорії вірогідності.

Метод повної взаємозамінності – це метод, за яким потрібна точність замикаючої ланки розмірного ланцюга досягається при включенні в нього або заміні в ньому будь-якої ланки без вибору або підгонки розміру.

При використанні методу не повної взаємозамінності потрібна точність замикаючої ланки розмірного ланцюга досягається не у всіх об’єктів, а тільки у певної їх частини.

2 – група – методи компенсації, використовуються тільки у збірних розмірних ланцюгах:

- метод регулювання;

- метод пригонки;

- метод селективної зборки.

3.) Метод розрахунку розмірних ланцюгів на максимум – мінімум

Для забезпечення повної взаємозамінності, потрібно навіть за найгірших сполученнях розмірів складових ланок отримати розмір замикаючої ланки у заданих межах. Цей принцип положено в основу методу розрахунку ланцюгів на максимум – мінімум.

Максимальний розмір замикаючої ланки:

.

Мінімальний розмір замикаючої ланки:

.

Різниця між максимальним та мінімальним розмірами – це допуск:

.

Таким чином, допуск замикаючої ланки дорівнює сумі допусків всіх складових ланок розмірного ланцюга.

Для визначення межових відхилень замикаючої ланки визначимо межові розміри у вигляді алгебраїчної суми номінального розміру та межового відхилення:

,

звідки:

.

Так як перші три члени правої частини у сумі дорівнюють нулю, то:

.

Аналогічно

.

Приклад. По заданому допуску кінцевого елементу провести розрахунок допусків та найбільших відхилень складових розмірного ланцюга методом повної взаємозамінності. Ескіз вузла наведено на рисунку 5.3 Всі елементи розмірного ланцюга мають симетричне розташування поля допуску відносно номінального розміру. Вихідні дані приведені в таблиці 5.1. В таблиці наведені розміри складових елементів , , , , та допуск кінцевого елементу .

Таблиця 5.1

Вихідні дані для розрахунку розмірного ланцюга

Параметри	,	,	,	,	,	,
Величина	70	6	56	4	2	0,4

Розв’язання задачі.

1). На основі рисунка 4.3, складається розрахункова схема розмірного ланцюга (рисунок 4.4).

У випадку повної взаємозамінності, зв’язок між допуском кінцевого елементу та допусками складових розмірного ланцюга можливо визначити рівнянням:

,

де - кількість всіх складових розмірного ланцюга, враховуючи кінцевий елемент.

Для наведеного прикладу:

.

Так як розміри складових розмірного ланцюга значно відрізняються одне від одного за величиною, то для них потрібно призначати допуски одного квалітету.

2. Визначається число одиниць допуску

,

де - величина одиниць допуску, вибирається з таблиці 1.7;

- середня величина розміру для інтервалу, в який входить розмір відповідного елементу розмірного ланцюга.

Тоді

.

Величина згідно з таблицею 3.1 відповідає 10 квалітету, для якого .

По таблицям полів допусків для валів та отворів [23] призначаються допуски на всі складові елементи по 10 квалітету. Так як збільшуючий елемент при обробці відноситься до отвору (відхилення зі знаком «+»), то для нього допуск береться як для основного отвору (по ). На зменшуючі розміри , та допуск береться як для основного валу (по ). Результати наведені в таблиці 5.2.

Таблиця 5.2

Допуски на складові елементи розмірного ланцюга по 10 квалітету

Параметри	,	,	,	,
Величина	120	48	100	48

.

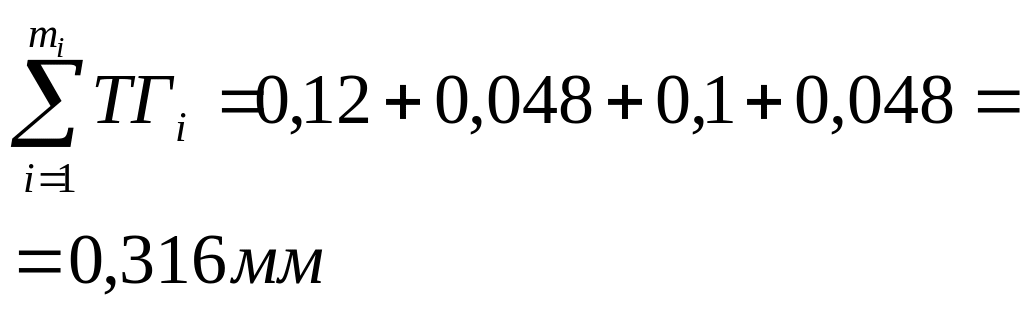Таким чином, не повністю використовується величина допуску кінцевого елементу . Тому більш раціонально буде назначити для елементів , та допуски по 10 квалітету, а для одного елементу дати більш широкий нестандартний допуск. Таким елементом в прикладі є елемент тому, що його точність в процесі виготовлення досягти найважче. Величина нестандартного допуску елемента вираховується

.

Таким чином, остаточні розміри складових елементів розмірного ланцюга мають відхилення, які наведені в таблиці 5.3.

Таблиця 5.3

Відхилення розмірів складових елементів розмірного ланцюга

Параметри	,	,	,	,
Величина

4). Особливості розрахунку площинних не лінійних та просторових розмірних ланцюгів

Розрахунок площинних не лінійних розмірних ланцюгів, як правило, зводять до розрахунку площинних лінійних розмірних ланцюгів шляхом проецирування всіх розмірів на один напрямок, найчастіше на напрямок замикаючої ланки.

Наприклад, для нормальної роботи зубчастої передачі від колінчастого валу до розподільчого валу необхідно витримати міжцентрову відстань (рис. 5.5) в межах заданого допуску.

Рисунок 5.5 - Площинний не лінійний розмірний ланцюг

Розмір залежить від розмірів , та які розташовані під кутами один до одного і складають площинний не лінійний розмірний ланцюг. Для приведення його до лінійного розмірного ланцюга всі розміри проецируються на напрямок замикаючої ланки (рис. 5.6).

Тоді рівняння розмірного ланцюга можливо записати у вигляді:

.

При розрахунках розмірного ланцюга за цим рівнянням номінальними розмірами ланок слід вважати:

.

Розрахунок просторових розмірних ланцюгів спочатку зводиться до розрахунку площинних шляхом проецирування на три взаємно перпендикулярні площини, а потім до розрахунку лінійних розмірних ланцюгів.

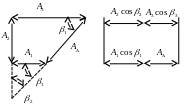
Рисунок 5.6 - Приведення площинного не лінійного розмірного ланцюга до лінійного

5.) Використання розмірного аналізу при ремонті машин

В процесі експлуатації машин розміри деталей змінюються в наслідок зносу та пластичних деформацій. В розмірних ланцюгах, де точність замикаючої ланки залежить від багатьох розмірів, це призводить до значних відхилень взаємного положення осей та поверхонь деталей, що значно погіршує якісні та економічні показники роботи машини.

Тому при ремонті машин важливо відновляти не тільки посадки сполучень деталей, а і точність замикаючих ланок розмірних ланцюгів. В більшості випадків не має потреби відновляти всі розміри, які входять в розмірний ланцюг. Як правило, можливо вибрати одну або дві ланки, за рахунок зміни розмірів яких відновлюється точність замикаючої ланки.

Задачею інженера-ремонтника є знаходження на основі кваліфікованого розмірного аналізу механізму ланки, зміною розмірів якої, можливо відновити первинну точність замикаючої ланки.

Питання для перевірки знань студентів.

1. Дати визначення розмірного ланцюга.

2. Види розмірного ланцюга?

3. Який розмір називають збільшуючим?

4. За якими ознаками визначають замикаючу ланку розмірного ланцюга?

5. Назвіть методи досягнення точності замикаючої ланки.

6. Сутність розрахунку розмірних ланцюгів на максимум – мінімум?

7. Якій величині дорівнює допуск замикаючої ланки?

8. Яким розрахунком забезпечується метод не повної взаємозамінності?

9. Яким розрахунком забезпечуються методи повної взаємозамінності?

10. Для чого робиться приведення площинного не лінійного розмірного ланцюга до лінійного?

11. Назвіть особливості розрахунку площинних не лінійних та просторових розмірних ланцюгів.

12. Принципи використання розмірного аналізу при ремонті машин.