Симплексные методы
Для реализации симплексных методов требуется, чтобы целевая функция была вычислима, должны быть заданы точность решения и начальный размер симплекса. Отличительной особенностью является направление поиска.
Поиск решения осуществляется с использованием симплекса.
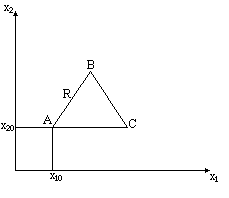
Симплекс – геометрический комплекс, имеющий n+1 вершину; где n – число факторов оптимизационной задачи. Для функции двух переменных n=2, а симплекс представляет собой треугольник на плоском пространстве переменных. Если этот треугольник равносторонний, то метод поиска называется методом регулярного симплекса. Когда начальный размер симплекса известен и равен R, координаты всех его вершин легко определить, если заданы координаты любой вершины, кА это показано в таблице. Пусть вершина А является начальной точкой поиска. Начиная поиск, определим координаты двух других вершин симплекса и вычислим значения целевой функции во всех трех вершинах. Сравним значения функции между собой и определим наихудшее (при поиске минимума – наибольшее, при поиске максимума – наименьшее). Дальнейший поиск следует предпринимать в направлении, противоположном той вершине, в которой наблюдается наихудшее значение функции. Для этого используется процедура отражения: ищем точку, зеркально отражая наихудшую вершину через противоположную сторону симплекса. Получаем новый симплекс, две из трех вершин которого принадлежат старому. Рассчитываем значение целевой функции в новой вершине и сравниваем его со значениями в двух других вершинах нового симплекса (эти значения были рассчитаны на предыдущем шаге решения). Вновь определяем наихудшее значение функции на новом симплексе, проводим процедуру отражения и ищем вершину следующего симплекса. Продолжая движение таким способом, мы неизбежно придем в область экстремума целевой функции, где при использовании процедуры отражения начнется вращение симплекса вокруг одной из его вершин. Если симплекс начал вращение и совершил (путем последовательных отражений вершин) полный оборот, то улучшить значение функции при движении симплекса начального размера уже не удастся. Необходимо уменьшить размер симплекса, разделив начальный размер на коэффициент сокращения, и продолжить решение задачи до достижения заданной точности.
y=F(x1;x2), R – начальный размер симплекса.
|
Х1 |
Х2 |
А В С |
Х10 Х10+R/2 X10+R |
X20
X20+ X20 |
Существует метод деформируемого симплекса, в котором отражение наихудшей вершины происходит через «центр тяжести» предыдущего симплекса, который определяется с учетом величины функции в его вершинах («тяжести» вершин). При использовании деформируемого симплекса поиск решения происходит еще более быстро по сравнению с методом регулярного симплекса.
Реальные поисковые оптимизационные задачи решаются с применением разных методов. Если при этом решение совпадает, то это увеличивает надёжность полученного решения. Поисковые методы не являются глобальными, поэтому если в ОДР существует два и более минимума, мы можем получить локальное решение вместо глобального.
Y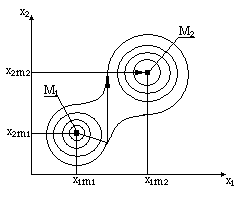
(M2)
< Y(M1)
глоб. лок.
То, какой из типов мы обнаружим, зависит от выбора начальной точки. Поэтому используют не только разные методы поиска, но проводят поиск из разных начальных точек.