2. Выполните действия:
-
а)
;
в)
;
б)
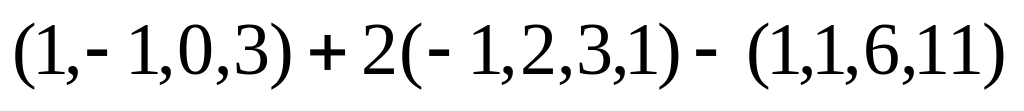;г)
.
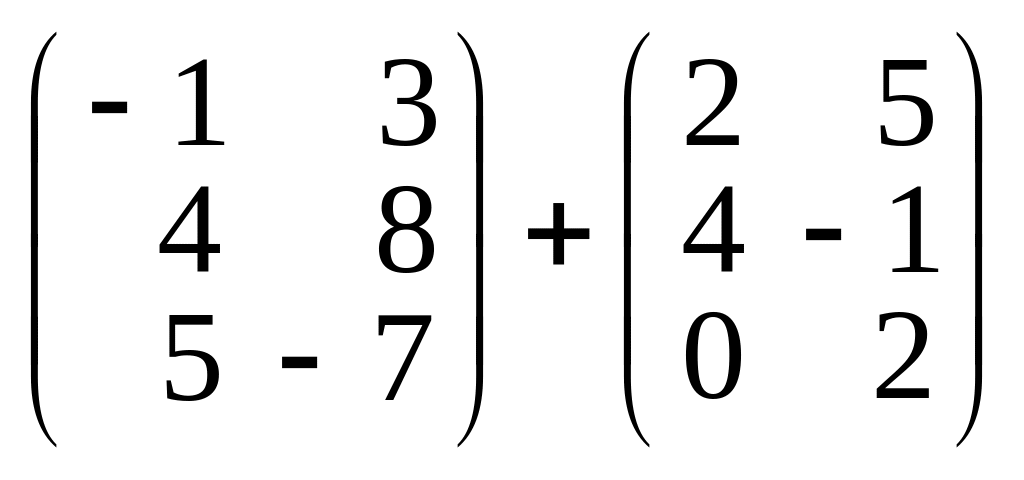3. Вычислите произведения матриц:
-
а)
;
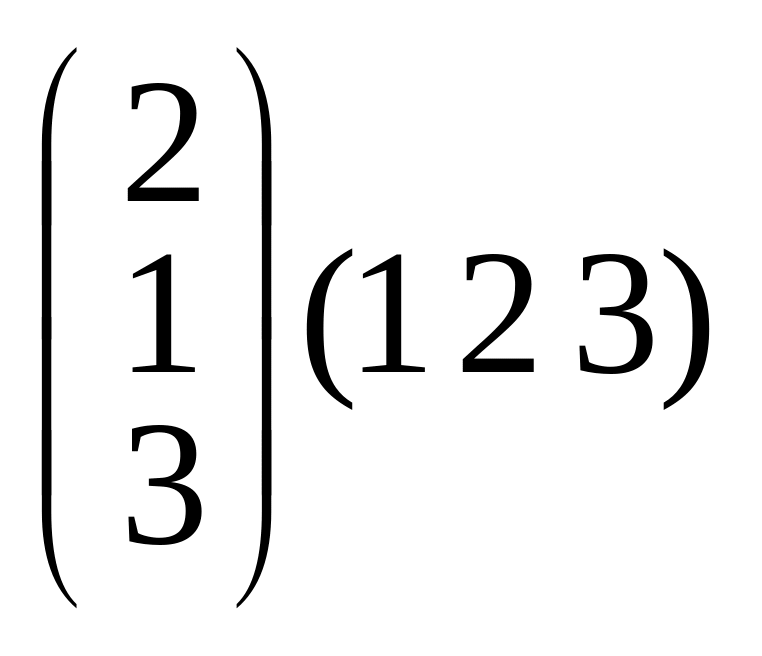б)
;
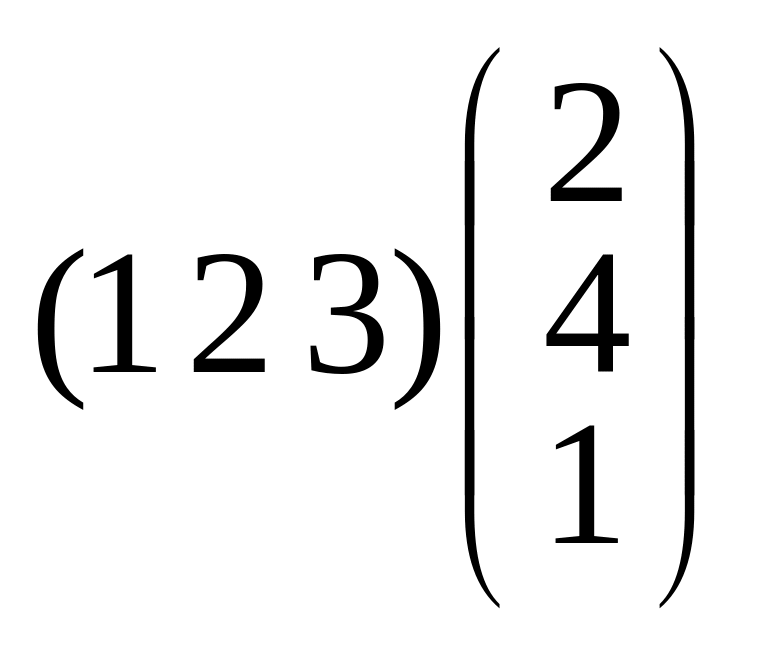в)
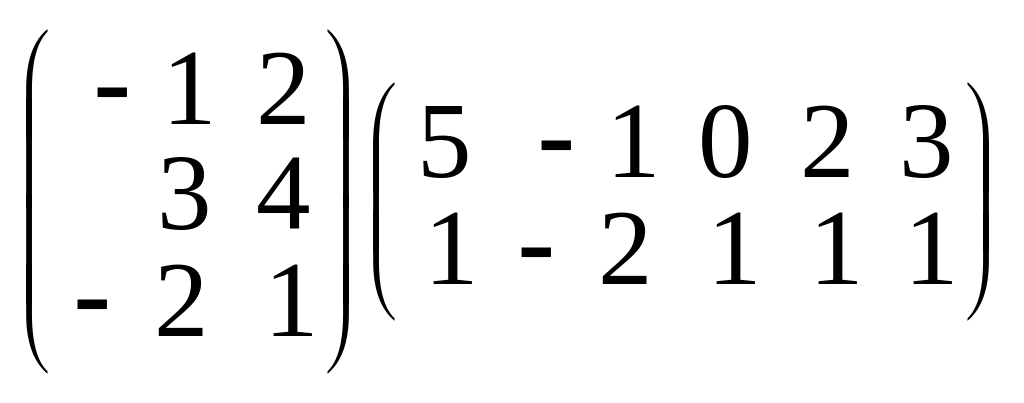;г)
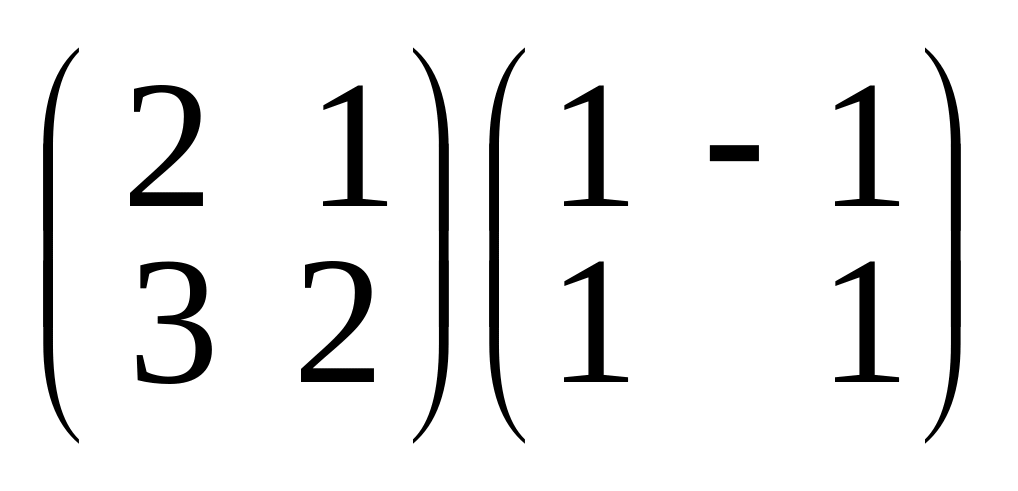;д)
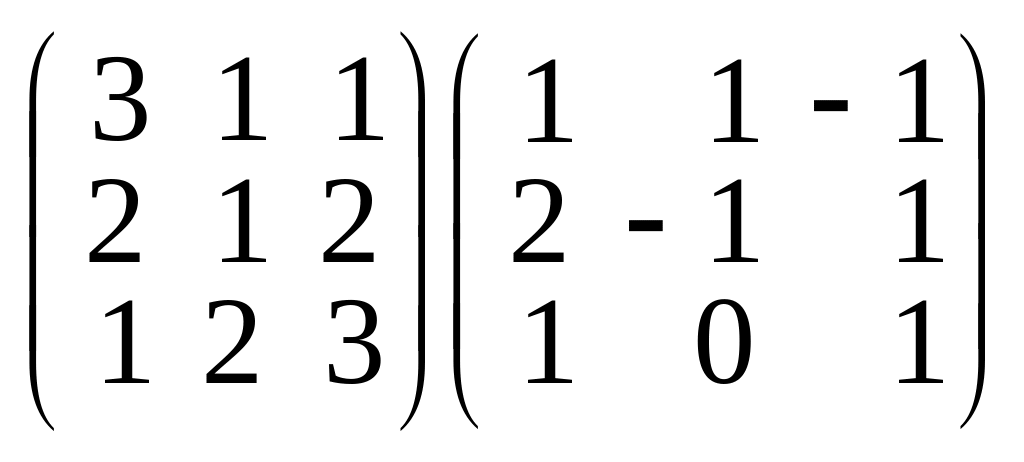;е)
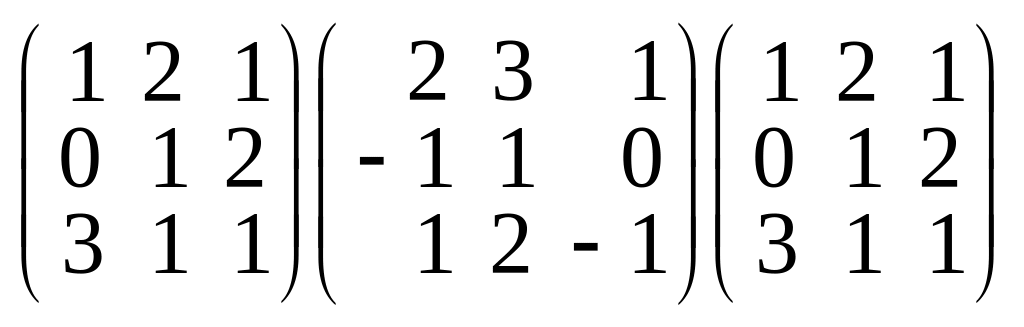;ж)
;з)
;и)
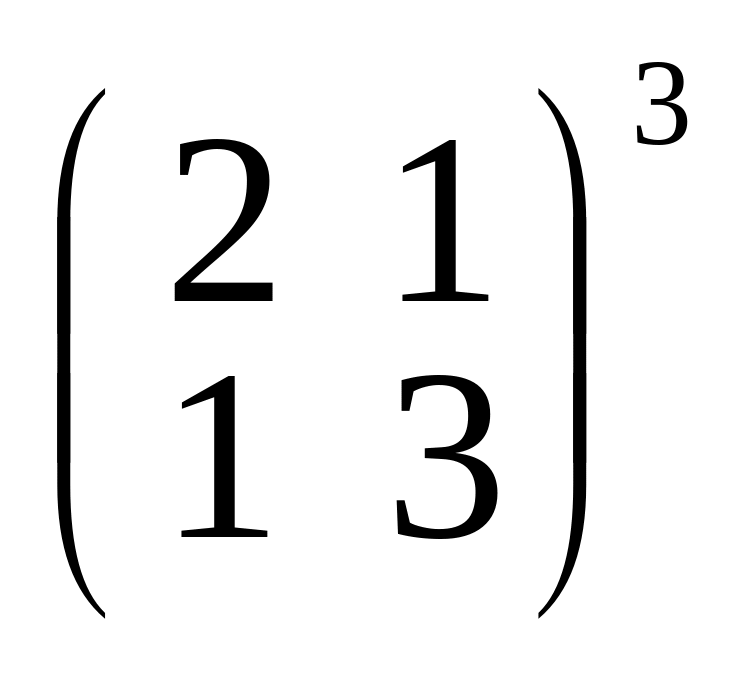;к)
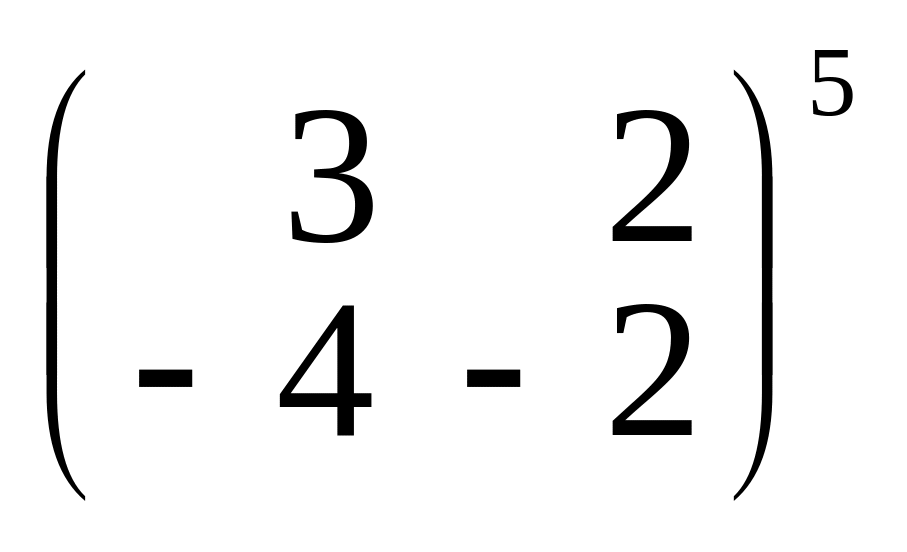;л)
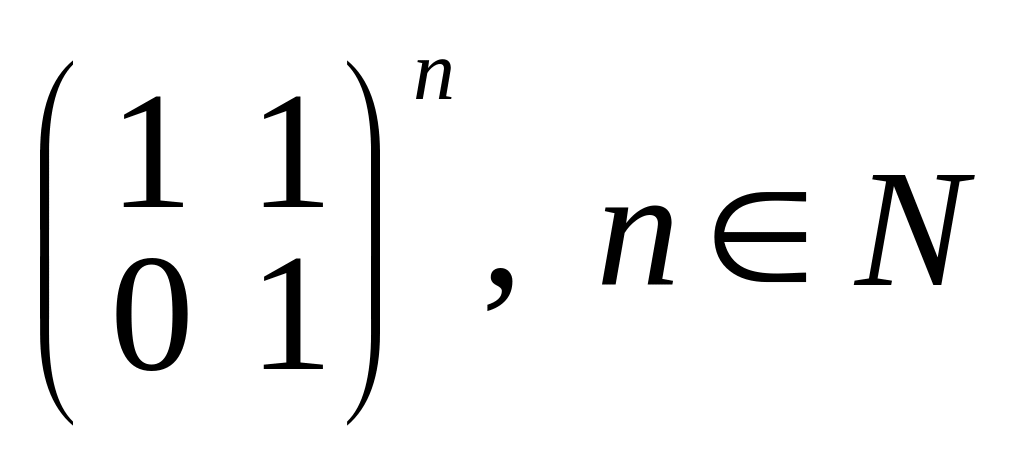;м)
;
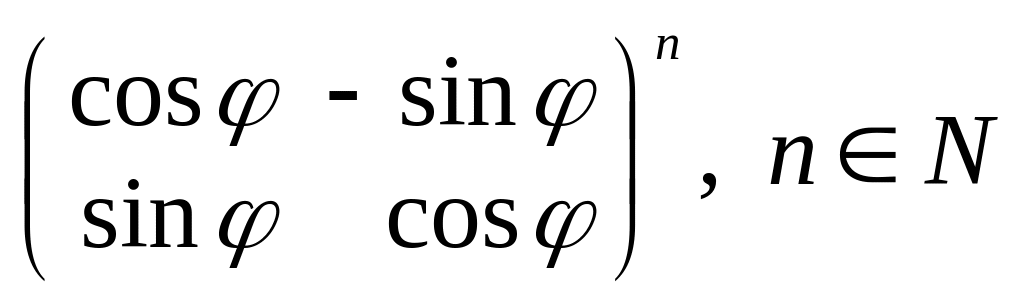н)
.
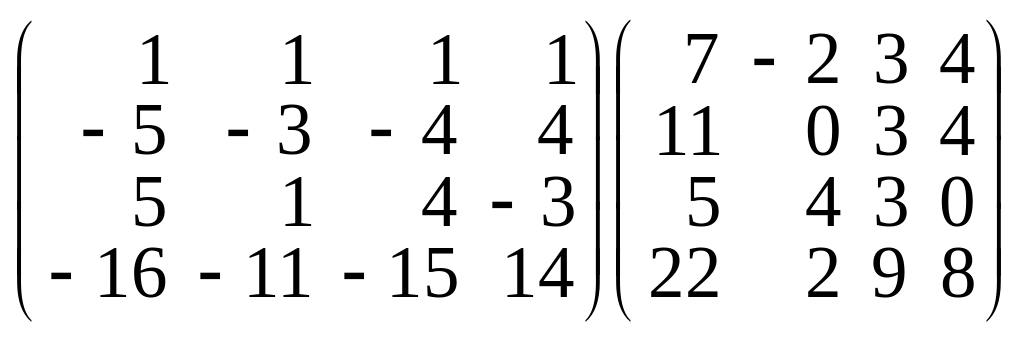4.
Используя равенство
вычислите
.
Самостоятельная работа
1. Докажите, что если для матриц А и В произведения АВ и ВА существуют и АВ = ВА, то матрицы А и В – квадратные одинакового порядка.
2. Покажите, что операция транспонирования обладает следующими свойствами:
а)
;
б)
;
в)
.
3.
Квадратная матрица называется
симметрической, если она не меняется
при транспонировании. Покажите, что
если А
симметрическая, то
симметрическая.
4.
При каком условии равенство
,
где А
и В
матрицы, является истинным?
5. Выполните действия:
-
а)
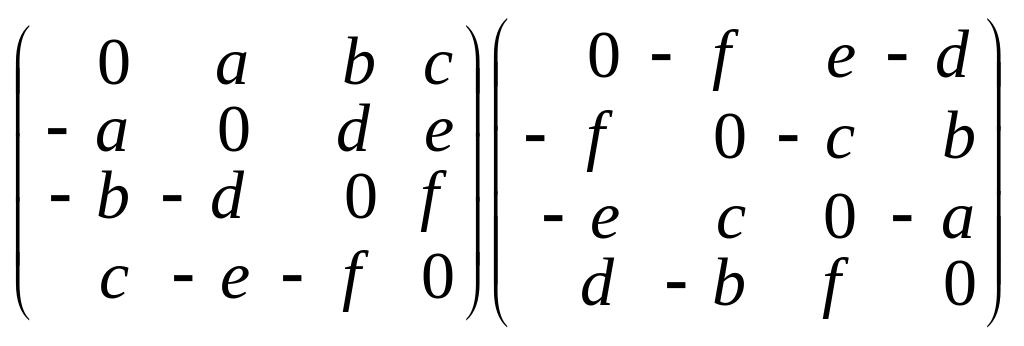;б)
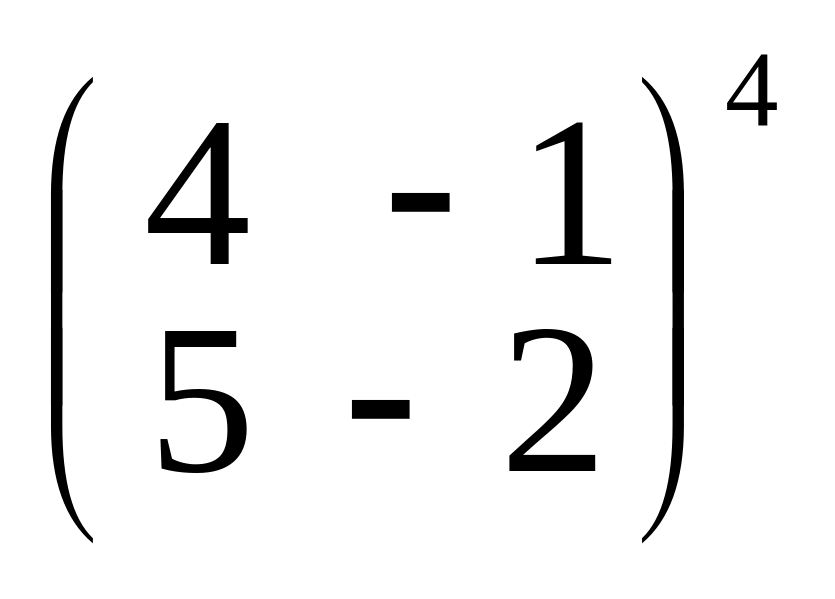;в)
;г)
.
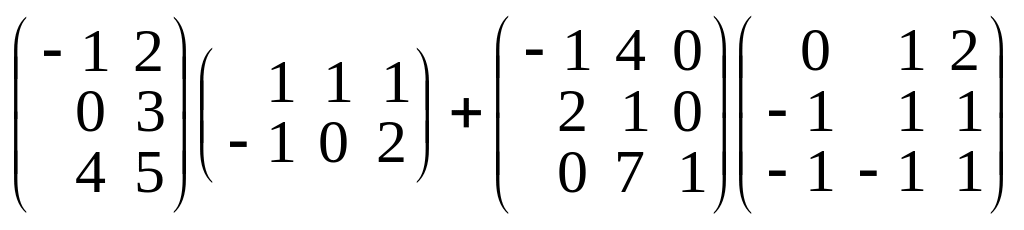6.
Вычислите
,
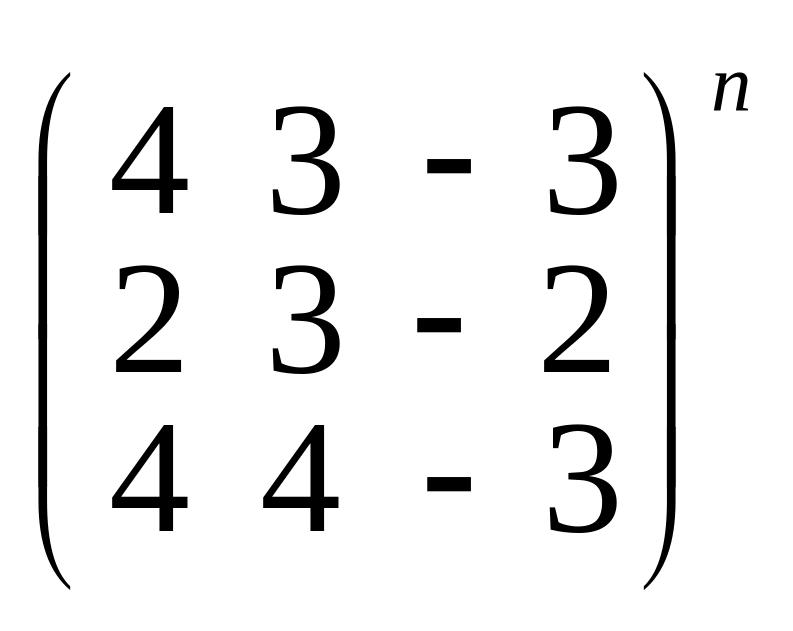используя равенство
.
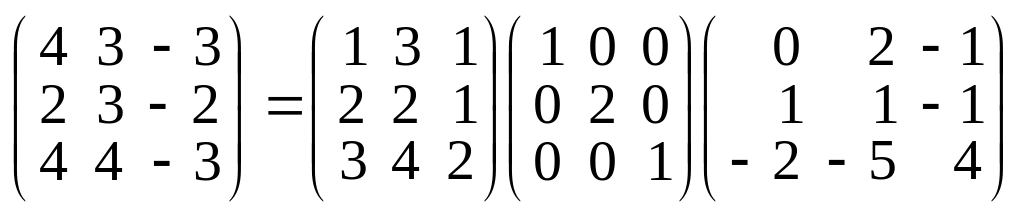7. Найти все матрицы перестановочные с матрицей:
а)
;
б)
;
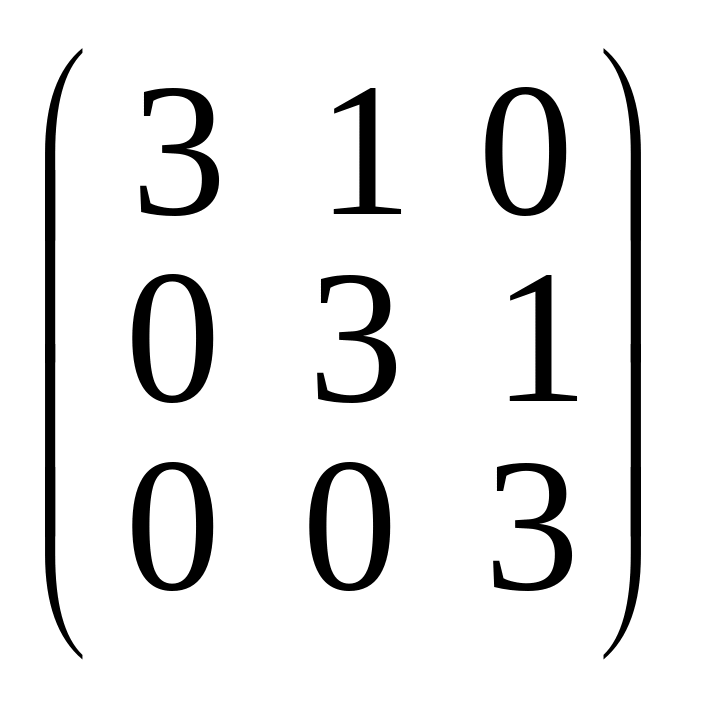в)
.
Задачи повышенной трудности
1. Вычислите .
2.
Найдите
(квадратная матрица n-го
порядка)
Тема 18. Перестановки и подстановки. Инверсии
Перестановкой
из n
элементов называется кортеж без
повторений всех элементов отрезка
натурального ряда
.
Общий
вид перестановки из n
элементов
,
где
.
Если в данной перестановке поменять местами два любых элемента, то эту операцию называют транспозицией.
Если в перестановке число a > b и число a предшествует числу b в записи перестановки, то числа a и b образуют инверсию ("беспорядок").
Если общее количество инверсий четно (нечетно), то перестановку называют четной (нечетной) перестановкой.
Известно, что транспозиция меняет четность перестановки.
Подстановкой из n чисел называют биективное отображение на себя.
Зрительно
подстановка представляет собой две
перестановки, записанные одна над
другой:
;
здесь
,
т.е. под элементом записывается его
образ.
Любую
подстановку можно записать в каноническом
виде, то есть в виде:
.
Подстановка называется четной (нечетной), если сумма инверсий в составляющих ее перестановках четная (нечетная).
Транспозицией подстановки называют перестановку двух ее столбцов. Транспозиция не меняет четность подстановки.
Практические задания
1. В какой перестановке чисел 1, 2, …, n число инверсий наибольшее и чему оно равно?
2. Если два элемента перестановки не образуют инверсию, будем говорить, что они образуют порядок. Чему равна сумма числа всех инверсий и всех порядков в любой перестановке чисел 1, 2, …, n?
3. Каково наибольшее возможное число инверсий в подстановке из n элементов, что это за подстановка?
Определите число инверсий в следующих перестановках:
4. (1, 9, 6, 3, 2, 5, 4, 7, 8);
5. (7, 5, 6, 4, 1, 3, 2);
6. (1, 3, 5, 7, …, 2n + 1, 2, 4, …, 2n);
7. (2, 4, 6, …, 2n, 1, 3, …, 2n – 1);
8. (2n, 2n – 2, …, 4, 2, 2n – 1, 2n – 3, …, 3, 1);
9. (1, 4, 7, 3n – 2, 2, 5, 8, …, 3n – 1, 3, 6, 9, …, 3n);
10. (3, 6, 9, …, 3n, 2, 5, 8, …, 3n – 1, 1, 4, 7, …, 3n – 2);
11. (2, 5, 8, …, 3n – 1, 3, 6, 9, …, 3n, 1, 4, 7, …, 3n – 2);
12. (2, 5, 8, …, 3n – 1, 1, 4, 7, …, 3n – 2, 3, 6, 9, …, 3n);
13. (1, 5, …, 4n – 3, 2, 6, …, 4n – 2, 3, 7, …, 4n – 1, 4, 8, …, 4n);
14. (1, 5, …, 4n – 3, 3, 7, …, 4n – 1, 2, 6, …, 4n – 2, 4, 8, …, 4n);
15. (4n, 4n – 4, …, 8, 4, 4n – 1, 4n – 5, …, 7, 3, 4n – 2, 4n – 6, …, 6, 2, 4n – 3, 4n – 7, …, 5, 1).
16. Для следующих подстановок выясните четны они или нет:
-
а)
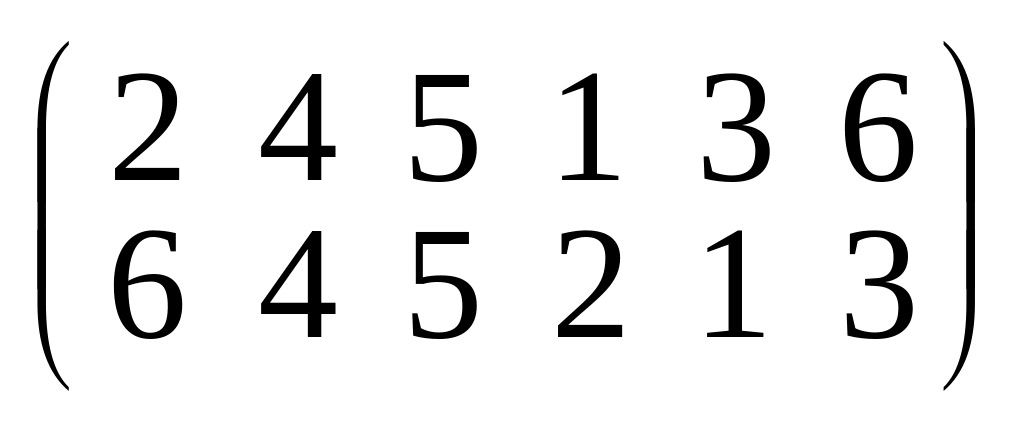;б)
;в)
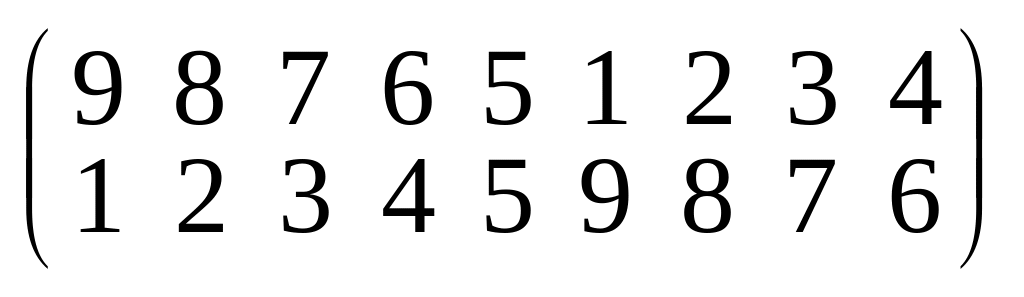;г)
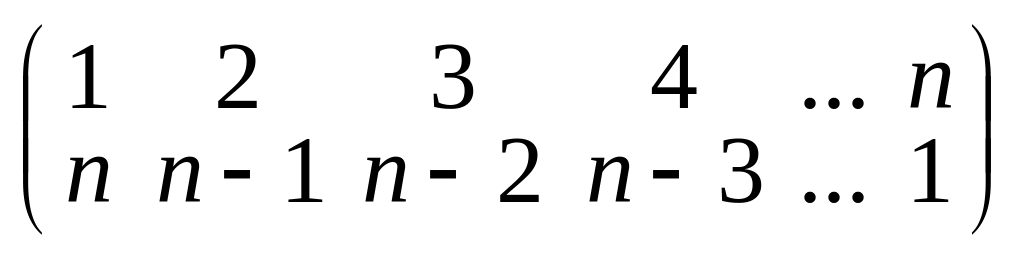;д)
.
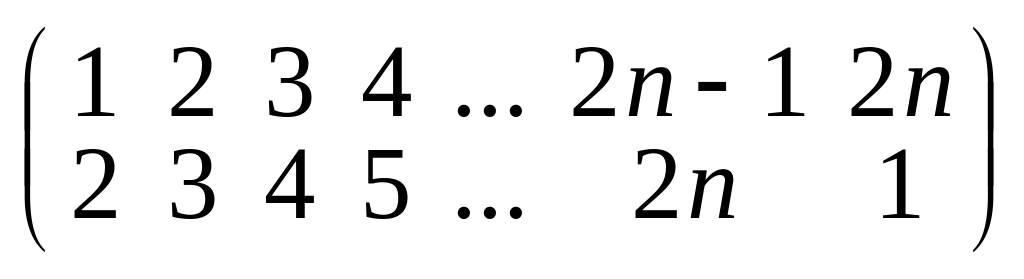