
- •Практические задания
- •6. Вычислите: .
- •7. Вычислите: .
- •9. Вычислите:
- •Самостоятельная работа
- •1. Вычислите
- •4. Выполните действия:
- •9. Укажите на плоскости множества точек, задаваемых следующими соотношениями:
- •10. Докажите, что а) б) .
- •Задачи повышенной трудности
- •Тема 13. Тригонометрическая форма комплексного числа. Извлечение корней из комплексных чисел
- •Практические задания
- •3. Вычислите: а) ; б) ; в) .
- •18. Вычислите .
- •Самостоятельная работа
- •Задачи повышенной трудности
- •Тема 14. Арифметические векторные пространства. Строчечный ранг матрицы
- •Практические задания
- •Самостоятельная работа
- •Задача повышенной трудности
- •Тема 15. Метод Гаусса решения систем линейных уравнений
- •Практические задания
- •Самостоятельная работа
- •Задачи повышенной трудности
- •Тема 16. Теорема КронекераКапелли
- •Практические задания
- •Самостоятельная работа
- •Задачи повышенной трудности
- •Тема 17. Матрицы и действия над ними
- •Практические задания
- •2. Выполните действия:
- •Самостоятельная работа
- •5. Выполните действия:
- •Задачи повышенной трудности
- •1. Вычислите .
- •Тема 18. Перестановки и подстановки. Инверсии
- •Практические задания
- •Самостоятельная работа
- •Задачи повышенной трудности
- •Тема 19. Определители
- •Практические задания
- •Самостоятельная работа
- •Задачи повышенной трудности
- •Тема 20. Решение систем линейных уравнений методом Крамера
- •Практические задания
- •Самостоятельная работа
- •Задачи повышенной трудности
- •Тема 21. Решение простейших матричных уравнений. Решение систем линейных уравнений матричным способом
- •Практические задания
- •Самостоятельная работа
- •Задачи повышенной трудности
- •Литература
Задача повышенной трудности
Пусть
А
и В
– матрицы с действительными элементами
и одинаковым количеством строк. Докажите,
что
![]()
Тема 15. Метод Гаусса решения систем линейных уравнений
Системой
линейных уравнений над полем Р
с переменными
![]() называется система
называется система

Матрица
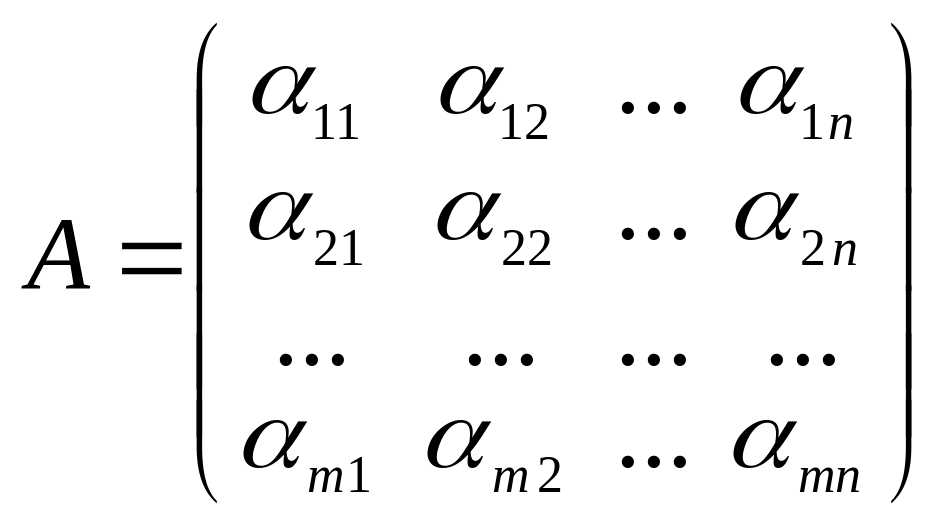 называется матрицей системы.
называется матрицей системы.
Матрица
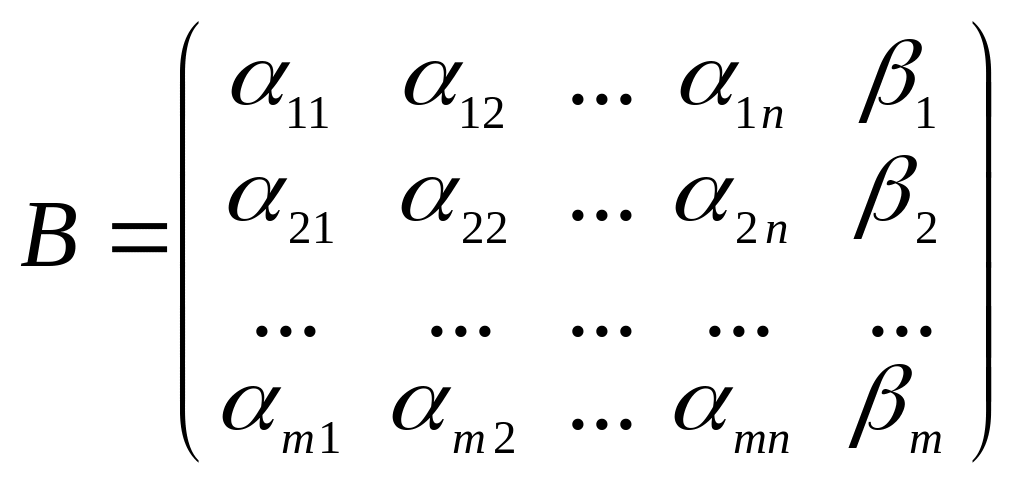 называется расширенной матрицей данной
системы.
называется расширенной матрицей данной
системы.
Две системы с одним и тем же количеством переменных называются равносильными, если множества решений их совпадают.
Элементарными преобразованиями системы называются следующие ее преобразования:
Р1. Перестановка двух уравнений системы.
Р2. Умножение всех членов некоторого уравнения на элемент поля Р, отличный от нуля.
Р3. Прибавление к некоторому уравнению системы другого уравнения, умноженного на некоторый элемент поля Р.
Р4.
Исключение из системы уравнения
![]() (если система не состоит исключительно
из одного этого уравнения).
(если система не состоит исключительно
из одного этого уравнения).
Как известно, преобразования Р1 – Р4 преобразуют данную систему в систему ей равносильную.
Первый ненулевой коэффициент уравнения называется ведущим коэффициентом уравнения.
Система называется ступенчатой, если ведущий коэффициент следующего уравнения (начиная со второго) является коэффициентом при неизвестном с большим номером, чем ведущий коэффициент предыдущего уравнения.
Систему
будем называть почти ступенчатой, если
последнее уравнение в ней
![]()
![]() ,
а подсистема без этого последнего
уравнения является ступенчатой.
,
а подсистема без этого последнего
уравнения является ступенчатой.
Ясно, что почти ступенчатая система несовместна, то есть множество ее решений пусто.
Ступенчатые системы легко решаются, начиная с последнего уравнения к первому.
Любую систему линейных уравнений можно привести к ступенчатой или почти ступенчатой системе с помощью элементарных преобразований.
Так как преобразования Р1 – Р4 системы соответствуют преобразованиям П1 – П4 расширенной матрицы системы, то рациональным методом является приведение расширенной матрицы В системы к ступенчатой матрице В /.
Если получив матрицу В /, вернуться к системе линейных уравнений, для которой В / будет являться расширенной матрицей системы, то мы и получим ту ступенчатую (или почти ступенчатую) систему, к которой сводится исходная система.
Практические задания
Решите следующие системы уравнений:
1.
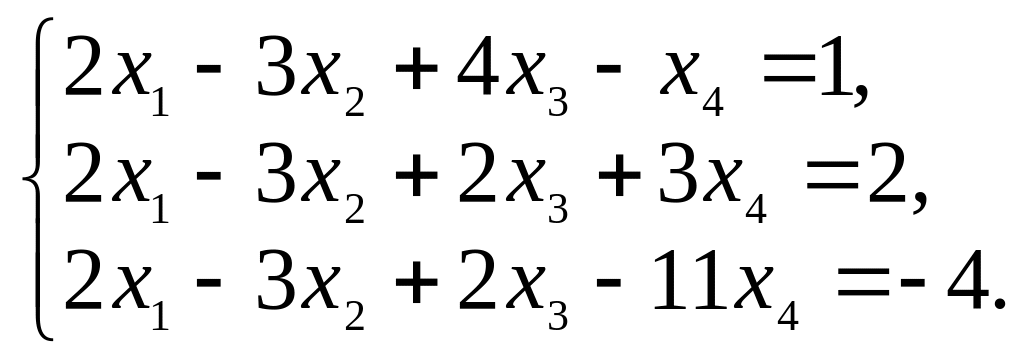 2.
2.

3.
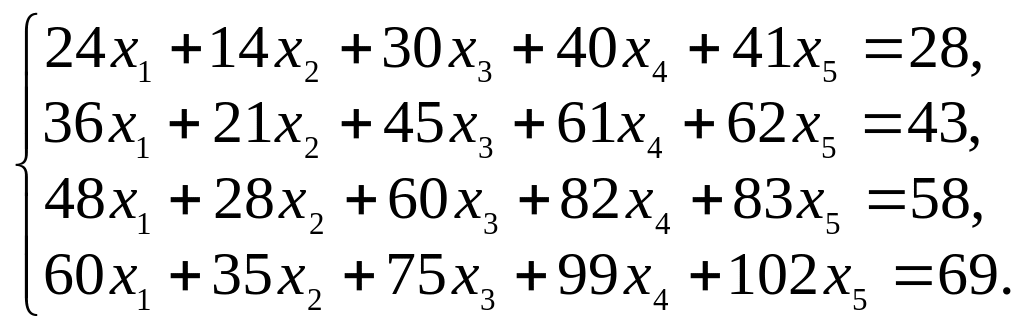
4.
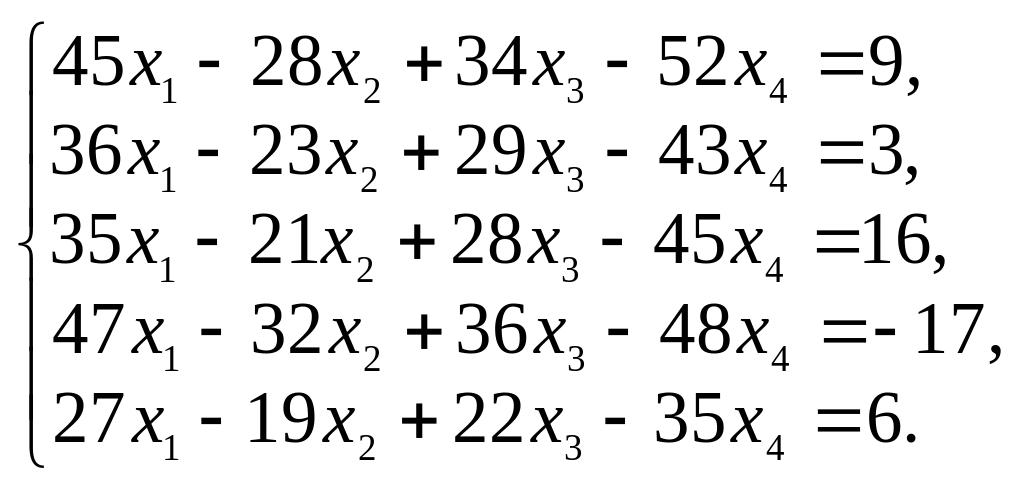 5.
5.
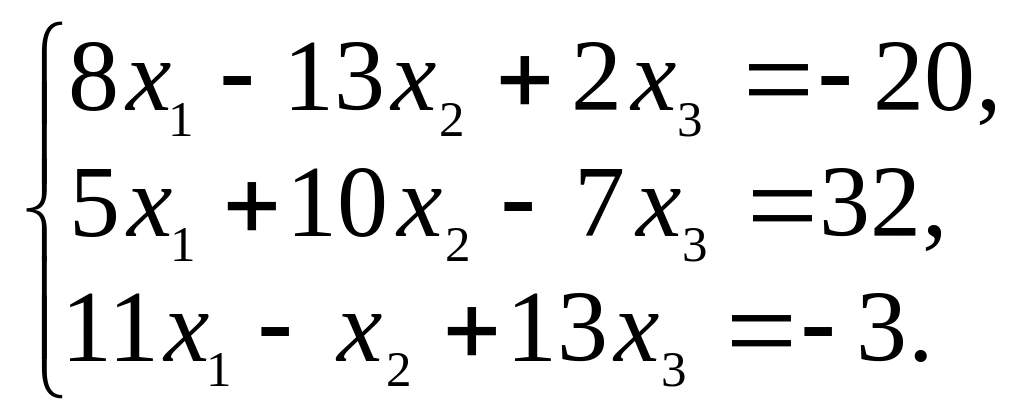
6. Решите следующие системы линейных уравнений:
а)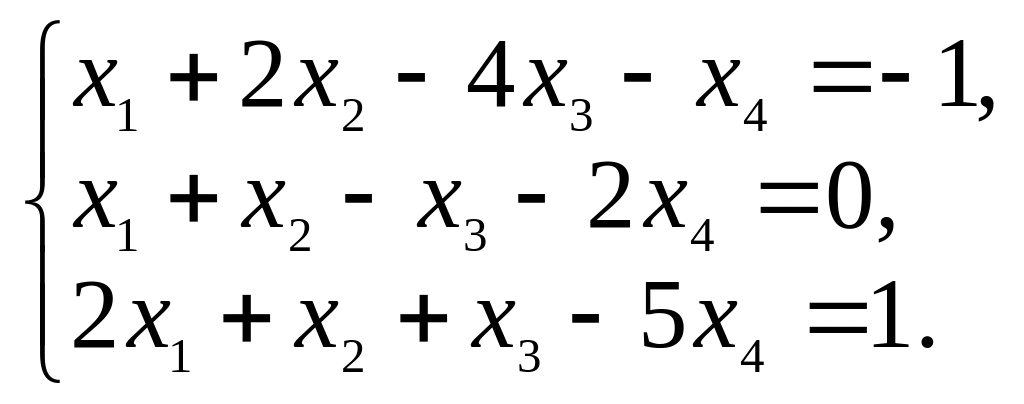 б)
б)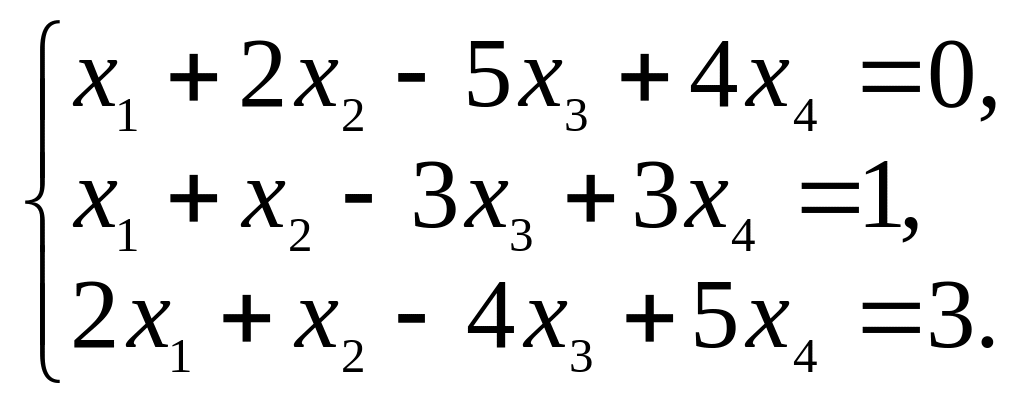 в)
в)
г) д)
д)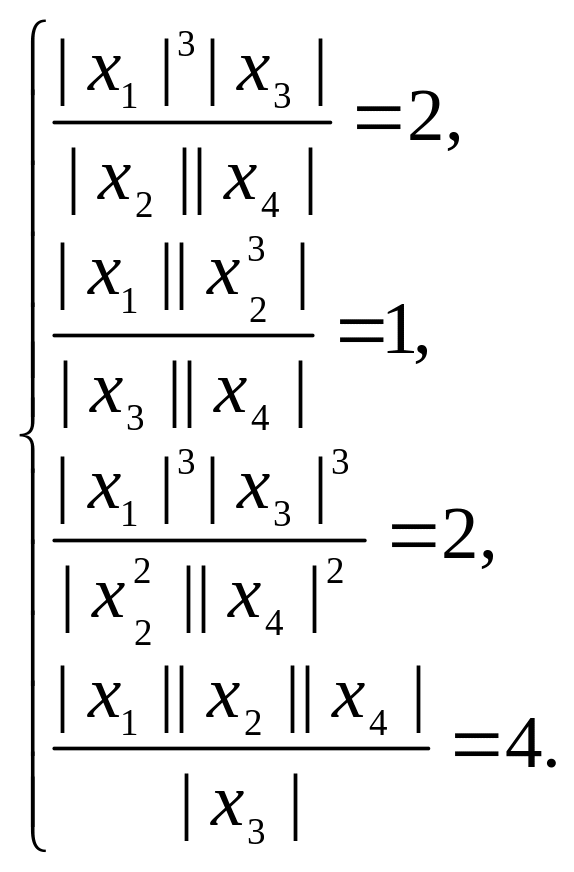
Самостоятельная работа
Решите системы уравнений:
1.
 2.
2.

3.
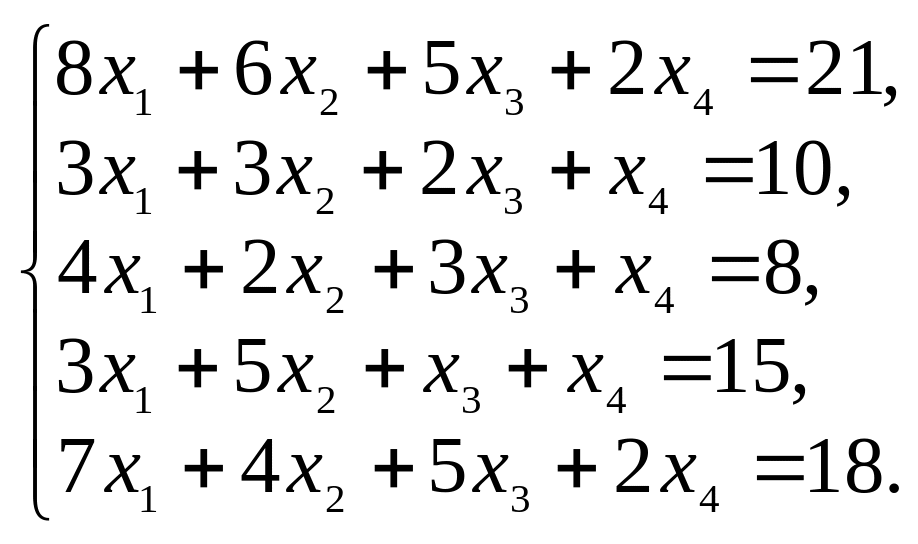 4.
4.
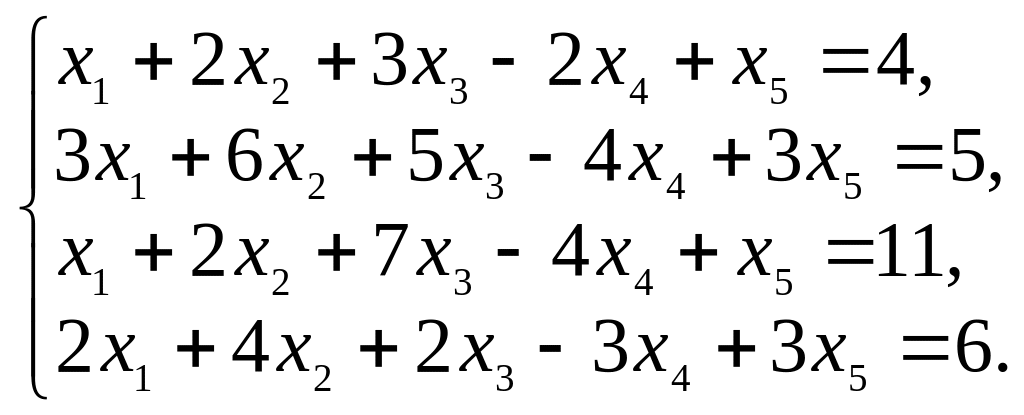
5.
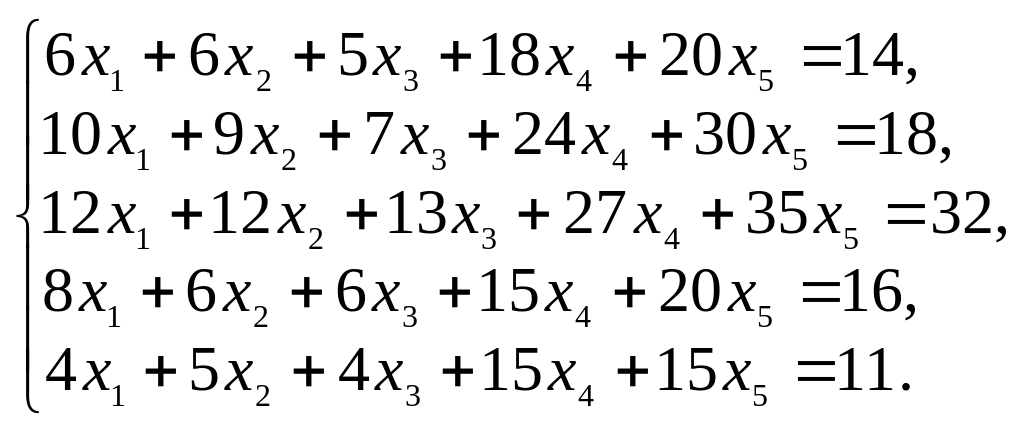 6.
6.
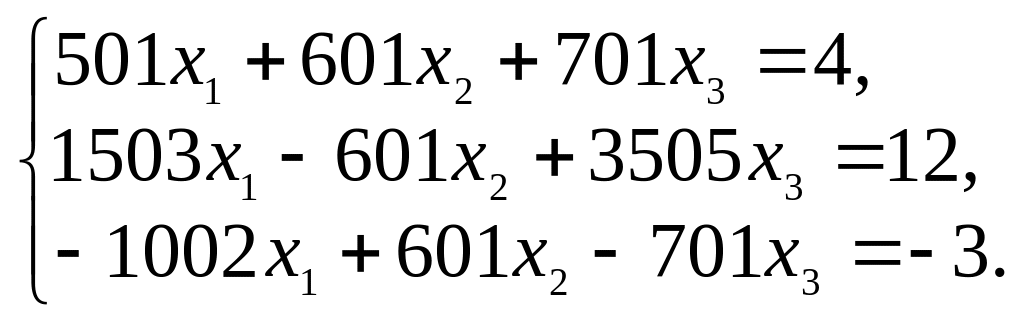
7.

Задачи повышенной трудности
1. Решите систему уравнений:
 если
,
,
,
попарно различные числа.
если
,
,
,
попарно различные числа.
2. Решите систему уравнений:

Тема 16. Теорема КронекераКапелли
Теорема КронекераКапелли. Система m линейных уравнений с n переменными является совместной тогда и только тогда, когда ранг расширенной матрицы системы совпадает с рангом матрицы системы. Система m линейных уравнений с n переменными имеет единственное решение тогда и только тогда, когда ранг расширенной матрицы системы и ранг матрицы системы равны n (то есть количеству переменных в системе уравнений).
