18. Вычислите .
19.
Упростите выражения: а)
б)
в)
.
20.
Найдите
,
если
21. Докажите, что cos 10 и sin 10 иррациональны.
22. Вычислите суммы:
-
а)
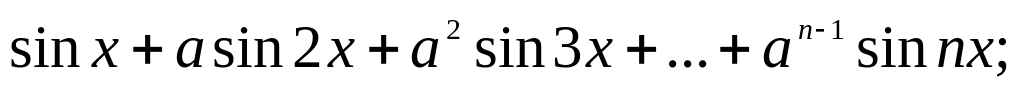
б)
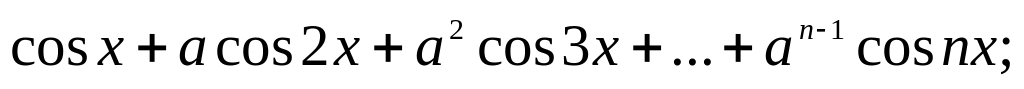
в)
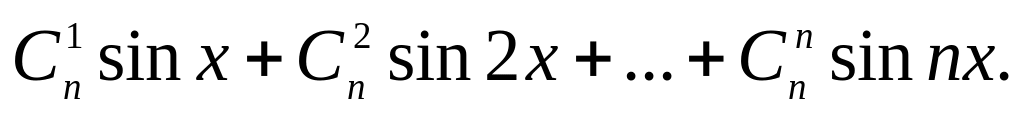
Самостоятельная работа
1. Представьте в тригонометрической форме следующие числа:
-
а) – 3;
б) 10;
в) – 2i;
г) 8i;
д) 2 – 2i;
е) 5 5i;
ж) 3 – 7i;
з)
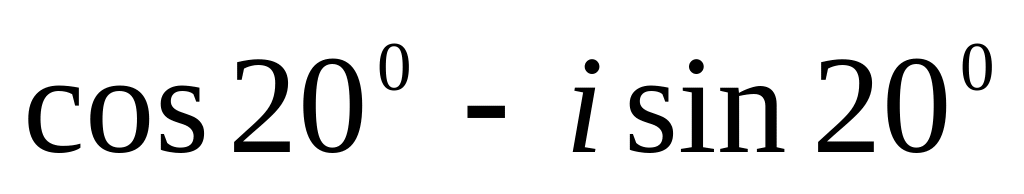;и)
.
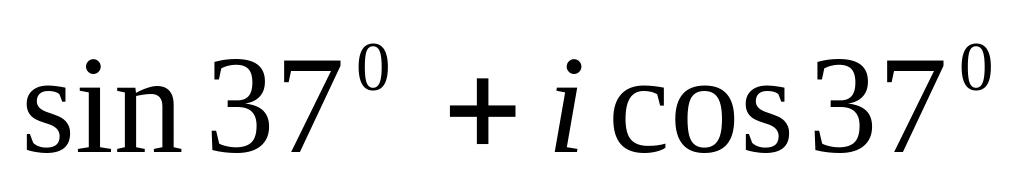2.
Вычислите: а)
;
б)
.
3. Выразите tg 9x через tg x.
4. Выразите через sin x и cos x: а) sin 7x; б) cos 7x; в) sin 9x; г) cos 9x.
5. Выразите ctg 7x через ctg x.
6.
Извлеките корни: а)
;
б)
;
в)
;
г)
;
д)
;
е)
.
7. Точки, изображающие корни 4-й степени из некоторого комплексного числа z соединили между собой. Что можно сказать о получившейся фигуре?
8. Пусть – корень 6-й степени из некоторого числа z. Найдите все корни 6-й степени из числа z.
9.
Покажите, что
10. Выразите в виде многочлена первой степени от косинусов и синусов углов, кратных х:
а) sin4x; б) cos4x; в) cos3x; г) sin6x.
11.
Найдите все комплексные корни уравнений:
а)
;
б)
.
12. Найдите сумму и произведение всех корней n-ой степени из 1.
13.
Найдите все комплексные числа,
удовлетворяющие условию
,
где n
N.
14.
Докажите, что если m
и n
– взаимно простые натуральные числа,
то существует только одно комплексное
число z,
удовлетворяющее системе
15. Докажите, что если m и n – взаимно простые натуральные числа, то произведение первообразного корня степени m из 1 на первообразный корень степени n из 1 есть первообразный корень степени mn из 1 и обратно.
Задачи повышенной трудности
1. Докажите, что следующая последовательность чисел
есть
геометрическая прогрессия и найдите
ее сумму.
2.
Является ли число
корнем некоторой степени из единицы?
Тема 14. Арифметические векторные пространства. Строчечный ранг матрицы
Множество
,
где Р
– произвольное поле называется n-мерным
арифметическим пространством, а его
элементы векторами, если в
определена
операция сложения
,
и умножение вектора на скаляр
:
.
Пусть
дана система векторов
.
Линейной комбинацией этой системы с
коэффициентами
называется
сумма
.
Комбинация
называется тривиальной, если
.
В
этом случае
.
Комбинация называется нетривиальной, если хотя бы один из коэффициентов отличен от нуля.
Система
векторов
называется линейно зависимой, если
найдется нетривиальная комбинация этой
системы, равная
.
Система
векторов
называется линейно независимой, если
только тривиальная комбинация этой
системы равна нулю (то есть, если система
линейно независима и
,
то
).
Известны следующие свойства линейно зависимых и линейно независимых систем:
1) система, содержащая линейно зависима;
2) система, содержащая два одинаковых вектора, линейно зависима;
3) система, содержащая два коллинеарных вектора, линейно зависима;
4) система векторов линейно зависима тогда и только тогда, когда хотя бы один вектор системы линейно выражается через остальные;
5) надсистема линейно зависимой системы линейно зависима;
6) непустая подсистема линейно независимой системы линейно независима;
7) одноэлементная система линейно зависима тогда и только тогда, когда ее элемент равен .
Таблица
вида
,
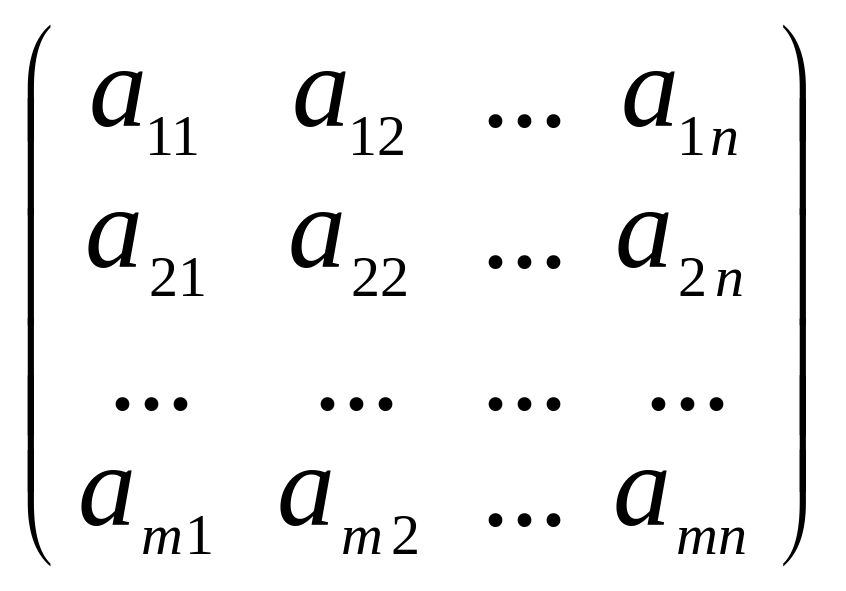где
,
называется матрицей размера
m
n.
Матрицу
можно рассматривать как совокупность
m
векторов, записанных один под другим:
Подсистема системы векторов (системы строк матрицы) называется максимальной линейно независимой системой, если она линейно независима, а всякая надсистема, получающаяся присоединением к ней других векторов системы (других строк матрицы) является линейно зависимой.
Количество векторов в максимальной линейно независимой системе называется рангом данной системы векторов (строчечным рангом матрицы).
Обозначив очевидную связь между матрицей и системой векторов, дальнейшее изложение будем вести в "матричных" терминах.
Следующие преобразования матрицы, называемые элементарными, не меняют ее ранга:
П1. Перестановка двух строк матрицы.
П2. Умножение строки матрицы на элемент поля 0.
П3. Прибавление к некоторой строке матрицы любой другой, умноженной на любой элемент поля.
П4. Удаление строки , то есть строки, состоящей из n нулей (если матрица не состоит исключительно из одной такой строки).
Первый ненулевой коэффициент матрицы называется ведущим коэффициентом строки.
Матрица называется ступенчатой, если ведущий коэффициент следующей строки (начиная со второй) находится в столбце с большим номером, чем ведущий коэффициент предыдущей строки.
В частности это означает, что в ступенчатой матрице нет строки .
Назовем матрицу почти ступенчатой, если последняя ее строка и после удаления этой строки матрица становится ступенчатой.
Ранг ступенчатой матрицы равен количеству строк в ней.
Для того чтобы выяснить каков строчечный ранг произвольной матрицы нужно с помощью элементарных преобразований привести ее к ступенчатой.
Для того чтобы выяснить, каков ранг данной системы векторов следует свести их в матрицу и найти строчечный ранг получившейся матрицы.
В практических задачах, говоря о ранге матрицы, имеем в виду строчечный ранг матрицы.