Одной
из геометрических интерпретаций
комплексного числа z
= a
+ bi
является точка М(a,b),
то есть абсцисса точки, изображающей
z,
есть Re
z,
а ордината ее есть Im
z.
Длина отрезка ОМ
=
называется модулем комплексного числа
z
и обозначается | z
|. Ясно, что
| z
|
0.
Другой
геометрической интерпретацией
комплексного числа z
= a
+ bi
является вектор
,
где О
– начало координат, а точка М
– первая интерпретация числа z,
то есть М(a,b).
Угол, образуемый вектором с положительным направлением оси Оx (действительной оси) называется аргументом комплексного числа и обозначается arg z (угол arg z отсчитывается от положительного направления оси Оx до вектора против часовой стрелки – в положительном направлении).
Ясно, что 0 arg z 2, а длина вектора это модуль комплексного числа.
Складываются
вектора по правилу параллелограмма, то
есть, если
изображает комплексное число z1,
комплексное число z2,
то сумма
+
,
вычисленная по известному правилу
сложения векторов изображает z1
+
z2.
Практические задания
1.
Вычислите
2.
Считая x
и y
действительными, найдите их из условия
.
3. Вычислите i36, i46, i125, i239, (i)25, (i)10, i10, i25.
4.
Выполните действия:
5.
Изобразите на комплексной плоскости
числа:
.
Найдите тангенс угла образованного
вектором, изображающим данное число с
положительным направлением оси Ох.
6. Вычислите: .
7. Вычислите: .
8.
Пусть
.
Вычислите:
.
9. Вычислите:
-
а)
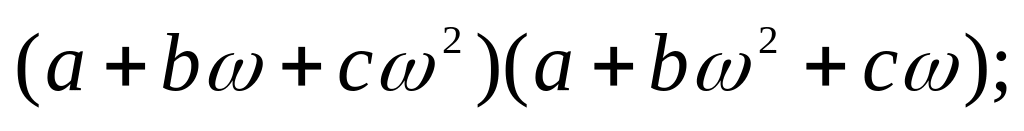
б)
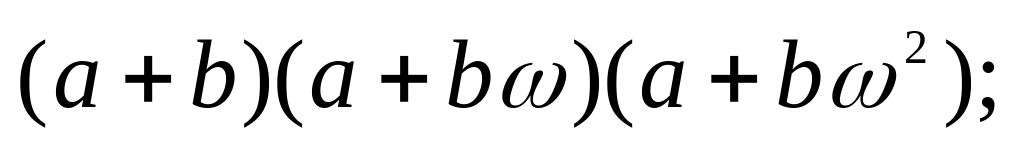
в)
,
где
.
10.
Найдите геометрическое место точек z
таких, что:
а)
;
б)
.
11.
Вычислите: а)
;
б)
;
в)
.
12. Найдите на плоскости точки, изображающие комплексные числа z такие, что z = t + (1 t)i, t R.
13. Изобразите на плоскости все комплексные числа z, для которых (1 + i)z действительно.
14. Вершины треугольника изображают числа z1, z2, z3. Какое число изображает точка пересечения всех медиан треугольника?
15. Укажите на плоскости множества точек, задаваемых следующими соотношениями:
-
а)
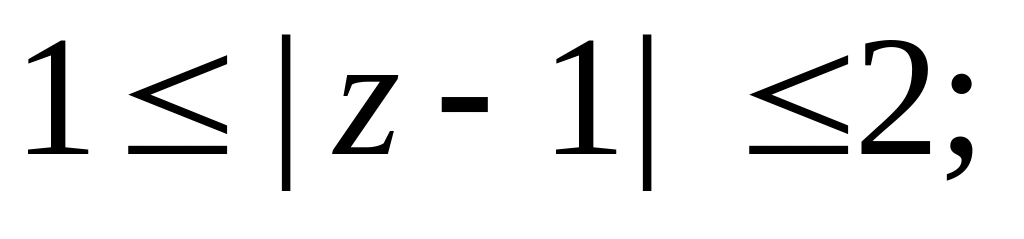
б)
в)
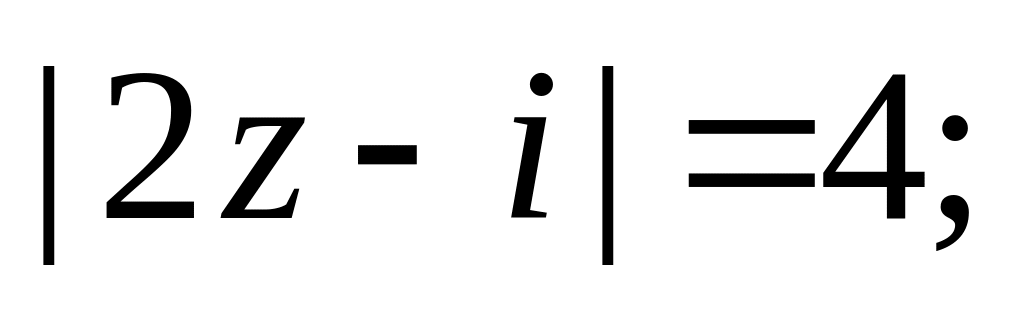
г)
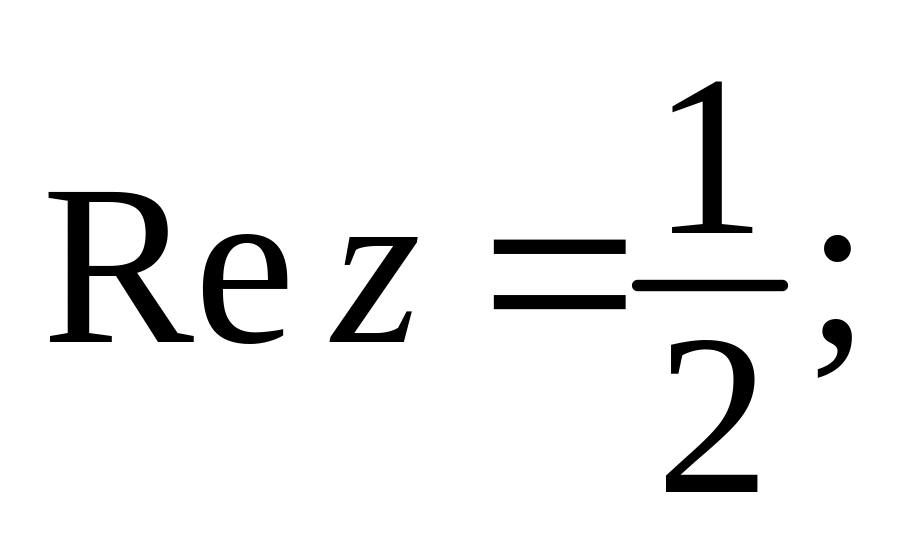
д)
е)
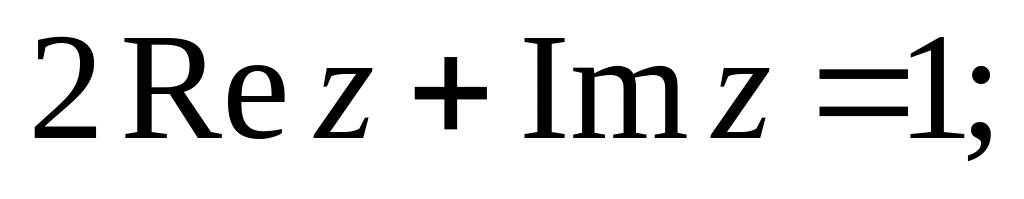
ж)
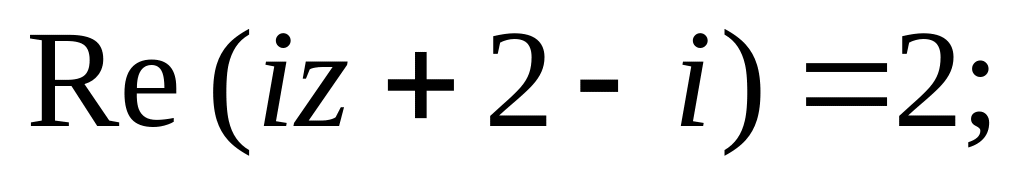
з)
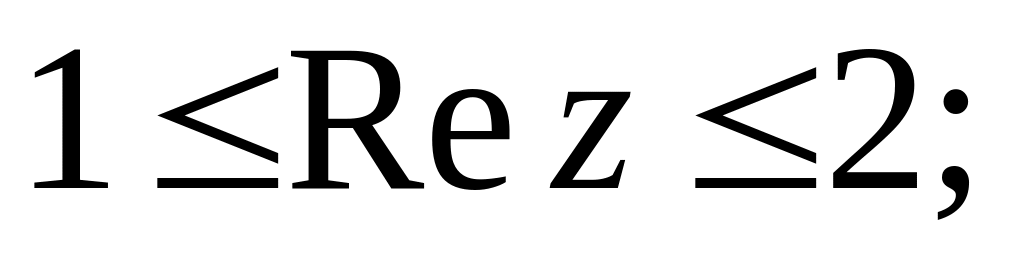
и)
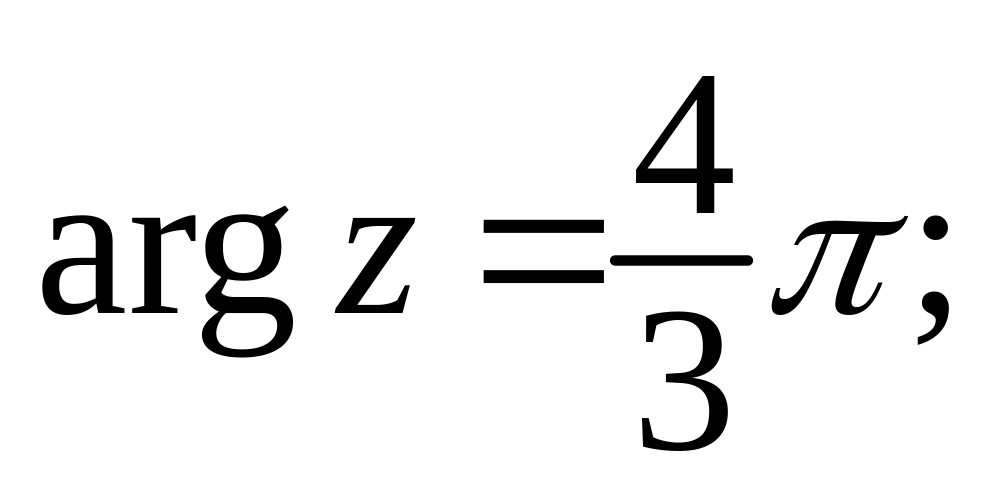
к)
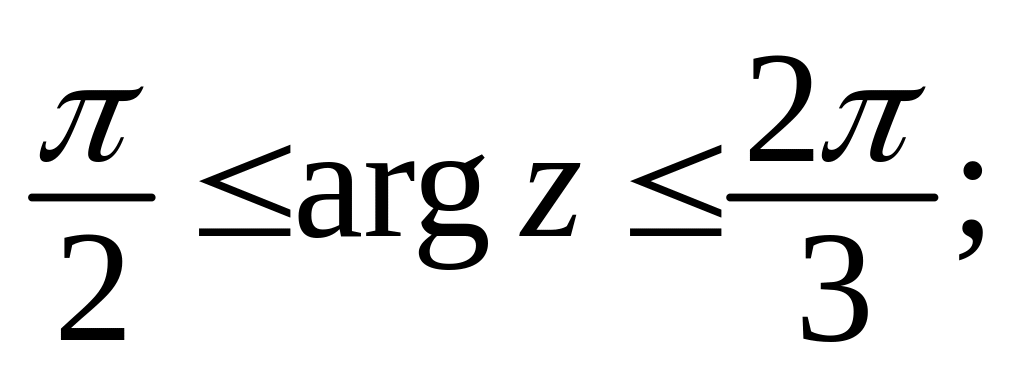
л)
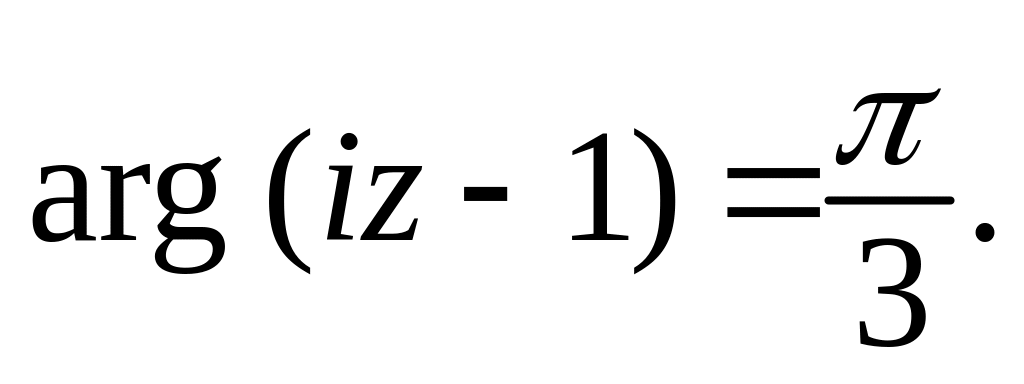
16.
Докажите, что а)
б)
.
17.
На комплексной плоскости найдите все
точки, изображающие комплексные числа
z,
удовлетворяющие следующим условиям:
а)
б)
в)
;
г)
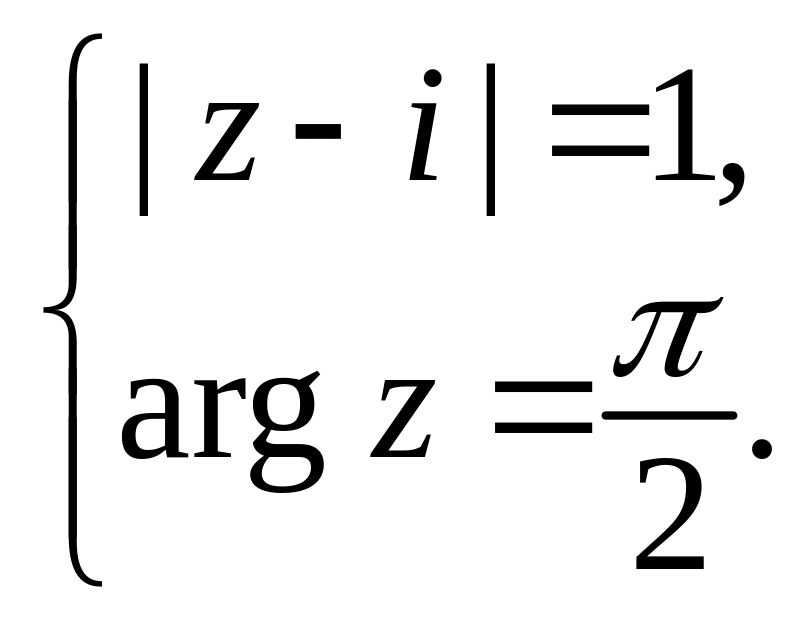
18. Решите уравнения:
-
а)
б)
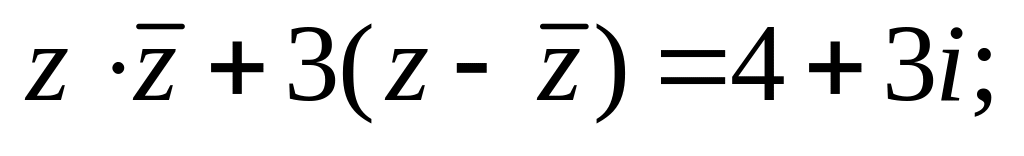
в)
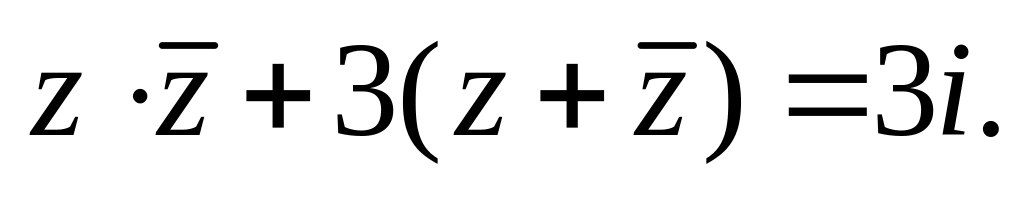
19.
Решите систему уравнений:
Самостоятельная работа
1. Вычислите
2.
Пусть А
и В
точки комплексной плоскости, изображающие
комплексные числа z1
и z2.
Докажите, что
3.
Найдите геометрическое место точек z
таких, что:
.
4. Выполните действия:
а)
б)
.
5.
Решите систему уравнений:
6.
Считая x
и y
действительными числами, найдите их из
условия
7. Концы некоторого отрезка изображают числа z и . Какое число изображает середина этого отрезка?
8. Точки А1, А2, А3 изображают комплексные числа z1, z2, z3. Найдите четвертую точку А4 такую, что эти точки станут вершинами параллелограмма и укажите число, изображаемое вершиной А4 (рассмотрите все варианты).
9. Укажите на плоскости множества точек, задаваемых следующими соотношениями:
-
а)
б)
в)
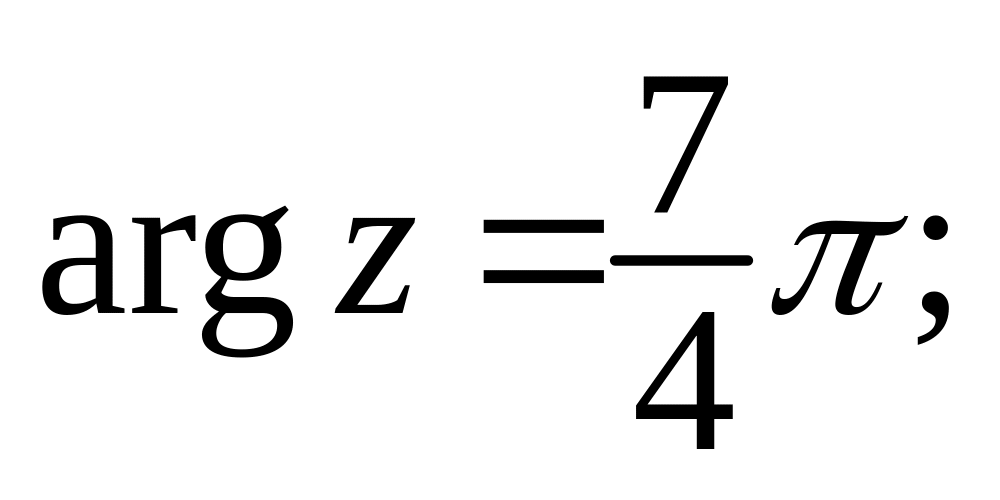
г)
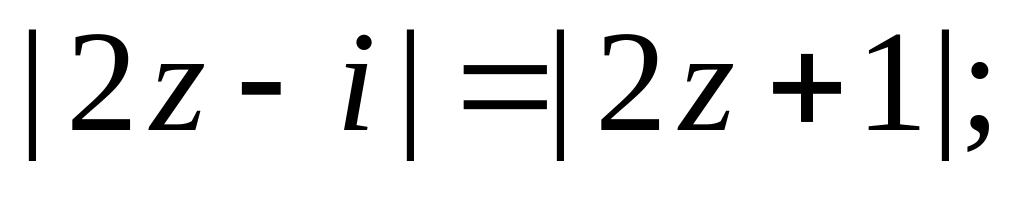
д)
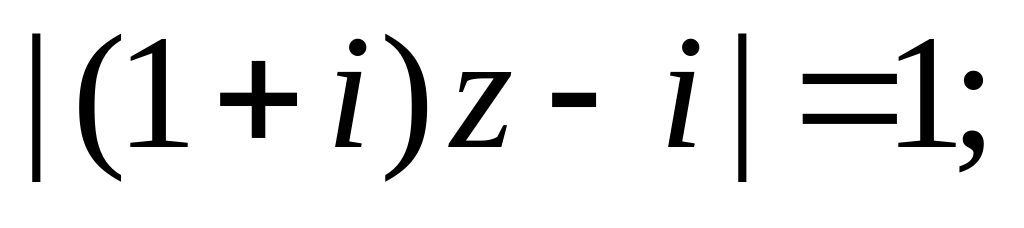
е)
ж)
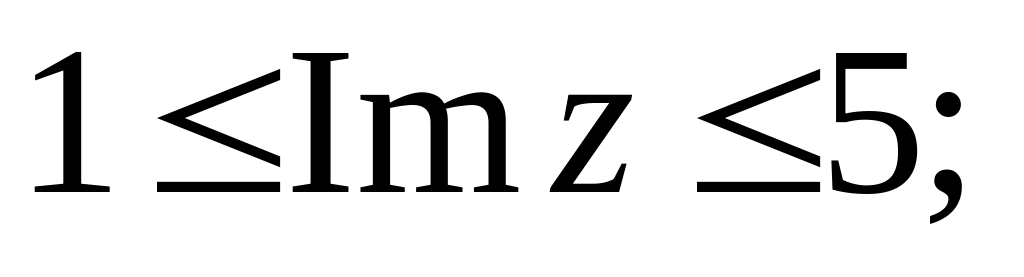
з)
и)
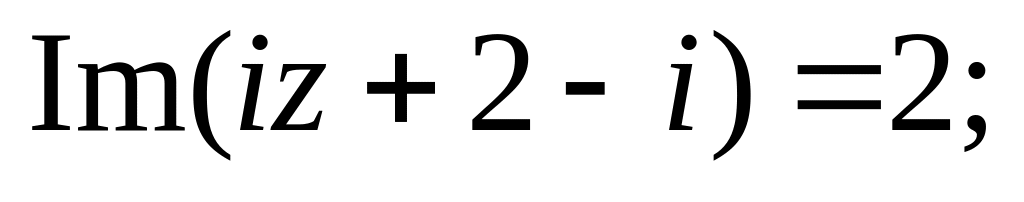
к)
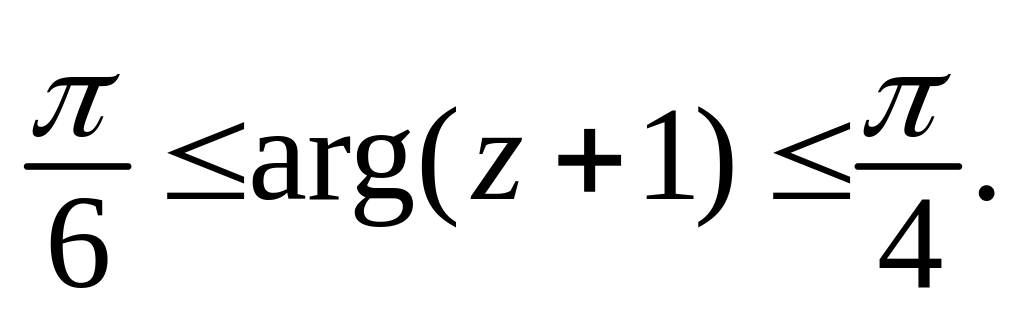
10. Докажите, что а) б) .
11. Докажите, что для любых целых чисел a, b, c, d произведение сумм квадратов (a2 + b2)(c2 + d2) можно представить как сумму квадратов k2 + l2 целых чисел k и l.
12.
На комплексной плоскости найдите все
точки, изображающие комплексные числа
z,
удовлетворяющие следующим условиям:
а)
б)
в)
г)
д)
.
13.
Решите уравнения: а)
б)
14.
Решите систему уравнений:
Задачи повышенной трудности
1.
Докажите тождество
и
укажите его геометрический смысл.
2.
Изобразите на плоскости множество
точек, соответствующих комплексным
числам
,
где t
R.