Практические задания
1.
Докажите основные равносильности
.
2. Постройте таблицы истинности для формул:
-
а)
;
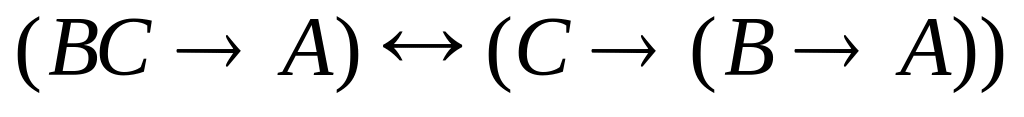б)
.
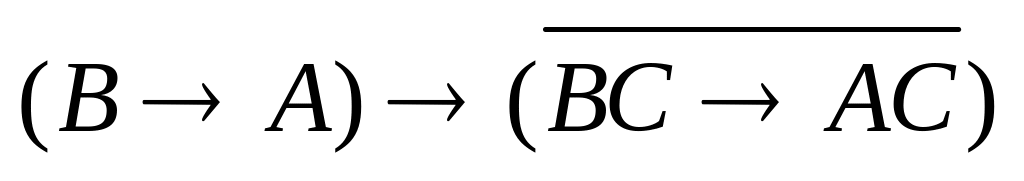3. Упростите формулы:
-
а)
;
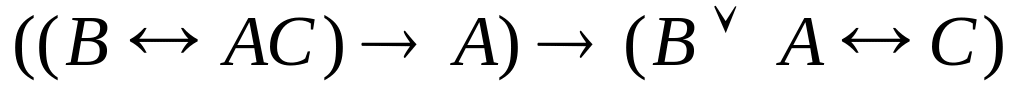б)
;
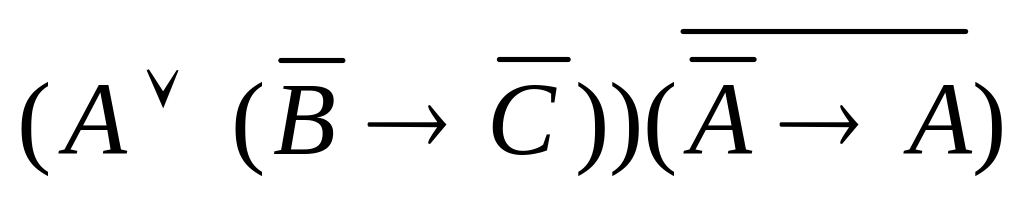в)
.
4. Логично ли рассуждение:
а)
А,
А
В╞
В;
б)
А
В,
В,
В╞
;
в)
А,
В,
А
В
,
╞
C?
5
.
Упростите схему
а) б)
6. Найдите истинностное значение формулы F в интерпретации :
а)
F
= (
)
(
B
C
D
C);
:
б)
F
= (A
B)(C
D)
(
B
C
);
:
7. Постройте наиболее простую схему из функциональных элементов, эквивалентную данной:
а)
б)
Самостоятельная работа
1. Постройте таблицы истинности для формул:
-
а) (АВ С) (А (
));
б) (
)
(
).
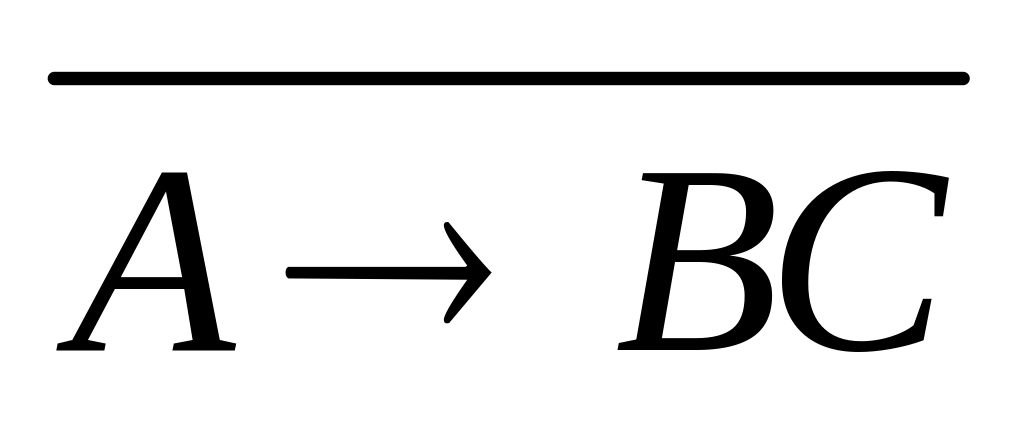2. Упростите формулы:
-
а) ((ВС А) (В А
))
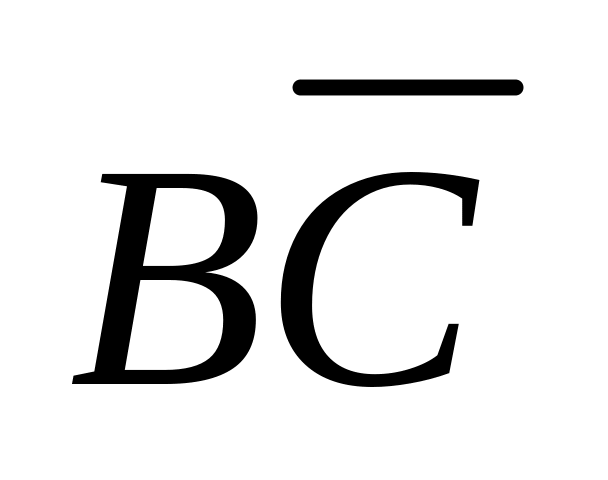ВС;
б) (( В) С) В(А );
в)
.
3. Логично ли рассуждение:
-
а) А В 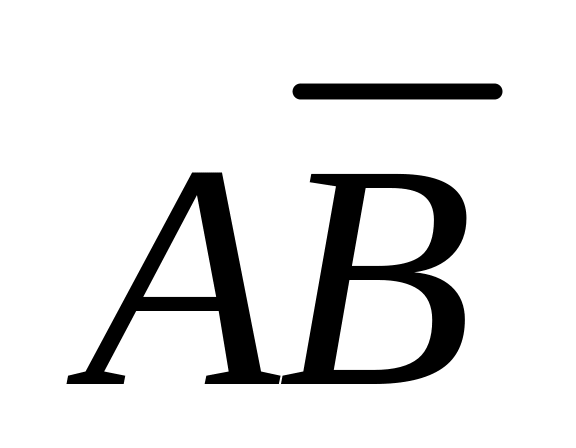С,
╞
С;
б) А, В С, А (В С)╞ АВ С?
4
.
Упростите схему
а) б)
5. Найдите истинностное значение формулы F в интерпретации :
а)
F
= (A(B
)
A
(B
C))
А
СD;
:
б)
F
=
C
((А
D)
(
В));
:
6. Постройте наиболее простую схему из функциональных элементов, эквивалентную данной:
а)
б)
Задачи повышенной трудности
1. Пусть в формуле F встречаются только операции отрицания, конъюнкции и дизъюнкции. Обозначим через F* формулу, которая получается из F заменой на и на , атомов на их отрицание, а отрицания атомов на сами атомы. Докажите, что F F* тавтология.
2. Пусть F – формула, в которой выделено некоторое вхождение формулы F1, пусть F* формула, которая получается из F заменой этого вхождения F1 на F2, причем F1 F2. Докажите, что F F* тавтология.
3. Было совершено ограбление. Трое бродяг Луи, Франсуа и Этьен дали инспектору Мегрэ следующие показания:
Л.: Чтобы обвинить меня, достаточно доказать, что Франсуа участвует в ограблении только тогда, когда в нем участвует Этьен, но я не виновен.
Ф.: Если Луи невиновен, то, чтобы обвинить меня достаточно признать Этьена тоже невиновным. Но Этьен виновен тогда и только тогда, когда виновен Луи. А если Этьен виновен, то я невиновен.
Э.: Виновен либо я, либо Франсуа и Луи.
Мегре знал, что Этьен всегда лжет, а Луи и Франсуа говорят правду. Кто причастен к ограблению?
4. В школьном шахматном турнире участвовал Иванов, Петров и Сидоров. Отца одного из них попросили быть судьей. Перед началом турнира его участники высказали следующие предположения:
И.: Не может быть, чтобы победили Петров и Сидоров вместе. Не может быть также, чтобы победил либо Петров, либо Сидоров. Значит, не смогу быть победителем и я.
П.: Если Иванов проиграет, то Петров будет победителем только тогда, когда выяснится, что Сидоров проиграл. Если Иванов проиграет, то проиграет и Сидоров. А я выиграть не смогу.
С.: Не может быть, чтобы проиграли и Иванов, и Петров, а я бы победил.
После окончания турнира выяснилось, что подтвердилось только высказывание сына судьи. Кто был победителем турнира? Как фамилия судьи?