Самостоятельная работа
1.
Докажите, что
.
2.
Дано
.
Докажите, что
.
3.
Дано
.
Докажите, что
.
4. Докажите неравенства:
-
а)
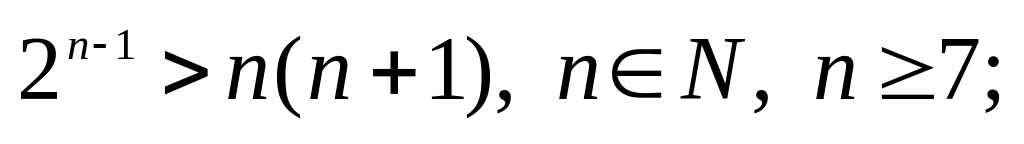
б)
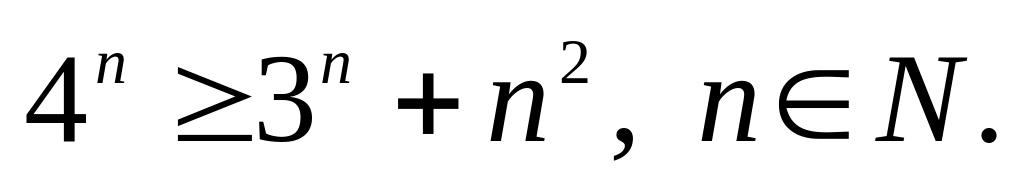
5.
Докажите формулу:
6.
Докажите, что если a
> b
> 0, то
7.
Докажите, что если a
> 0, b
> 0, то
8.
Докажите, что
9.
Числа последовательности
определяются следующими условиями
.
Докажите, что
.
10.
Пары чисел
образуются по закону
.
Докажите, что
11. Докажите тождества:
-
а)
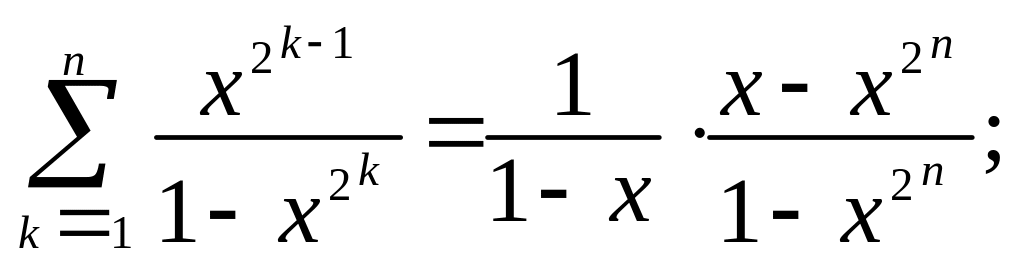
б)
.
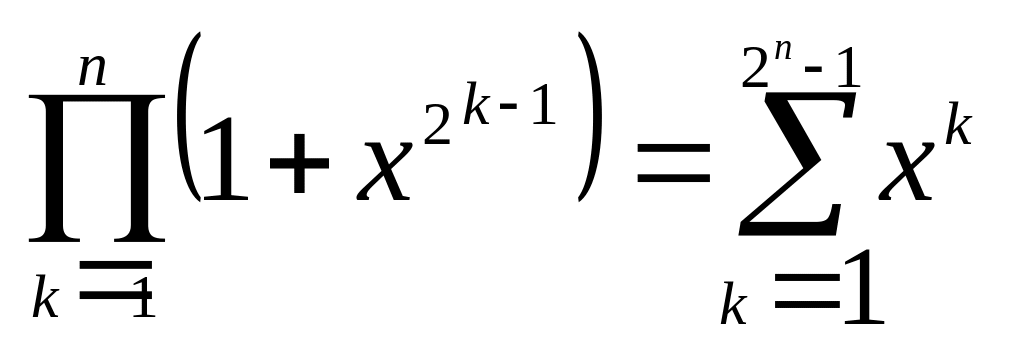12. Последовательность Фибоначчи определяется условиями: . Докажите следующие соотношения:
-
а)
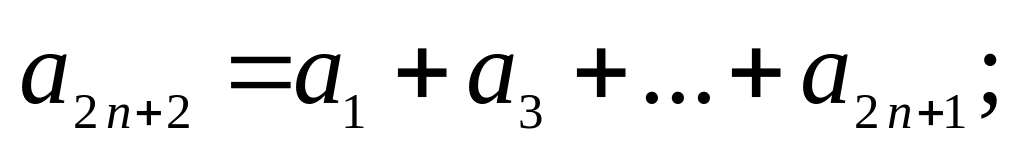
б)
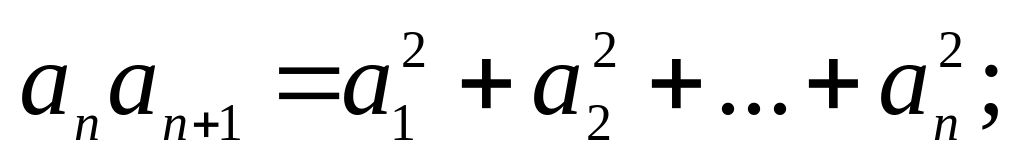
в)
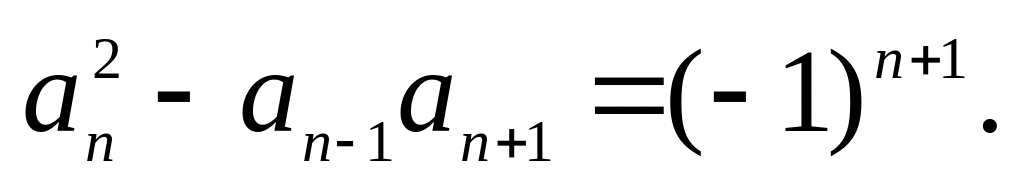
13.
Последовательность задана условием:
.
Докажите, что для всех n
N
имеет место неравенство
.
14. Докажите, что для всех n N справедливы следующие неравенства:
а)
;
б)
;
в)
.
15. Найдите ошибку в следующем рассуждении: Если на свете есть хотя бы один блондин, то все люди блондины. В самом деле, для n = 1 утверждение справедливо, так как по условию есть блондин. Допустим, что любая группа численностью не превышающей k человек состоит из одних блондинов. Рассмотрим теперь произвольную группу из k + 1 человек. Разобьем ее на две произвольные части численностью a и b человек в каждой. Ясно, что a k и b k. На эти группы распространяется индуктивное предположение. Следовательно, в каждой из них – одни блондины. Поэтому рассматриваемая группа состоит из одних блондинов. Итак, утверждение справедливо для n = 1; из предположения о справедливости для n k следует справедливость его для n = k + 1. Утверждение доказано.
16.
Докажите тождество
.
17. На сколько частей делят плоскость n прямых, никакие две из которых не параллельны и никакие три не пересекаются в одной точке?
18.
Докажите:
где
> 1,
0, n
– натуральное число, большее единицы.
19.
Докажите, что при всяком натуральном n
число
делится на 84.
20.
Докажите, что
.
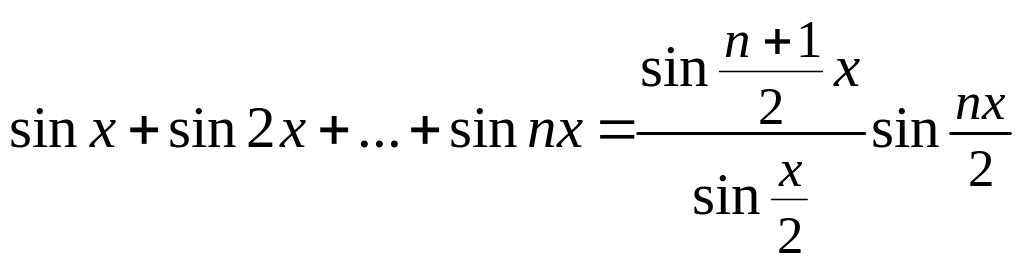21.
Докажите, что
справедливо для всех натуральных n.
22. Найдите ошибку в следующем рассуждении: Все числа равны между собой. В самом деле, при n = 1 утверждение справедливо: число равно самому себе. Допустим, что утверждение справедливо для n = k, то есть любые k чисел равны между собой. Рассмотрим теперь произвольное множество из k + 1 чисел. Перенумеруем все эти числа номерами 1, 2, …, k + 1. Первые k чисел равны между собой и поэтому равны первому числу. Исключим второе число. Тогда оставшиеся k чисел, среди которых есть и (k + 1)-е число, равны друг другу и равны первому числу. Утверждение, таким образом, справедливо и для n = k + 1. Итак, утверждение справедливо для n = 1 и из предположения о его справедливости для n = k выведена его справедливость для n = k + 1. Утверждение доказано.
Задачи повышенной трудности
1.
Доказать, что для любых целых положительных
чисел
справедливо неравенство
.
2.
Доказать, что при любом n
> 1 справедливо неравенство
.