
- •Практическая работа №1
- •Краткие теоретические сведения
- •Последовательность решения задачи:
- •И сходные данные
- •Практическая работа №2
- •Краткие теоретические сведения
- •Последовательность решения задачи:
- •И сходные данные
- •Практическая работа №3
- •Краткие теоретические сведения
- •Теорема Пуансо
- •Теорема Вариньона
- •Последовательность решения задачи:
- •И сходные данные
- •Практическая работа № 4
- •Краткие теоретические сведения
- •Последовательность решения задачи.
- •И сходные данные
- •Лабораторная работа № 1
- •Краткие теоретические сведения
- •Установка для испытания
- •Отчёт по работе
- •Практическая работа № 5
- •Краткие теоретические сведения
- •Общие теоремы динамики точки
- •Последовательность решения задачи:
- •И сходные данные
- •Практическая работа №6
- •Краткие теоретические сведения.
- •Последовательность решения задачи:
- •Исходные данные
- •Практическая работа №7
- •Краткие теоретические сведения.
- •Последовательность решения задачи:
- •Исходные данные
- •Пример решения задачи:
- •Практическая работа №8
- •Краткие теоретические сведения.
- •Последовательность решения задачи:
- •Исходные данные
- •Пример решения задачи:
- •Практическая работа №9
- •Краткие теоретические сведения.
- •Последовательность решения задачи:
- •Исходные данные
- •Практическая работа № 10
- •Краткие теоретические сведения
- •Исходные данные
- •Последовательность решения задачи:
- •Лабораторная работа № 3
- •Порядок выполнения работы:
- •Содержание отчета:
- •Практическая работа № 11
- •1. Определение исполнительных размеров для восстановления изношенной червячной передачи. Распознавание элементов зацепления:
- •2 Геометрический расчет червячной передачи:
Практическая работа №1
Тема: определение реакций связей для тел, находящихся в равновесии под действием плоской системы сходящихся сил.
Цель: научиться определять вероятные направления и вычислять реакции связей твердых тел, нагруженных плоской системой сходящихся сил.
Краткие теоретические сведения
В статике твердого тела рассматриваются две основные задачи:
1. Сложение сил и приведение системы сил, действующих на твердое тело, к простейшему виду.
2. Определение условий равновесия действующих на твердое тело системы сил
 Равновесие
несвободных твёрдых тел изучается в
статике на основании аксиомы: всякое
несвободное тело можно рассматривать
как свободное, если отбросить связи и
заменить их действие силами реакций
этих связей( или для краткости, реакциями
этих связей).
Равновесие
несвободных твёрдых тел изучается в
статике на основании аксиомы: всякое
несвободное тело можно рассматривать
как свободное, если отбросить связи и
заменить их действие силами реакций
этих связей( или для краткости, реакциями
этих связей).
3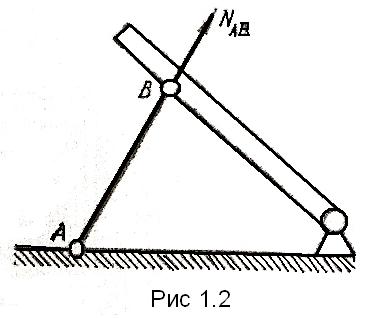 .
При решении задач будем различать
следующие виды связей (опорных закреплений
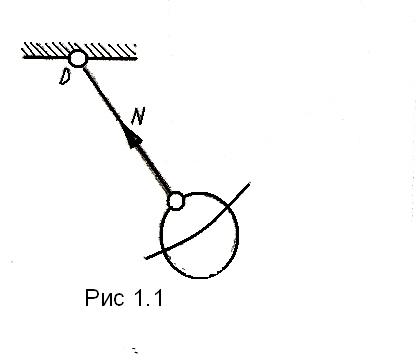
, или опор): Нить (рис 1.1). Реакция N
натянутой нити направлена вдоль неё к
точке подвеса.
.
При решении задач будем различать
следующие виды связей (опорных закреплений
, или опор): Нить (рис 1.1). Реакция N
натянутой нити направлена вдоль неё к
точке подвеса.
4.
Невесомый стержень с шарнирами по концам
(рис 1.2) реакция
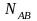 направлена вдоль его оси.
направлена вдоль его оси.
5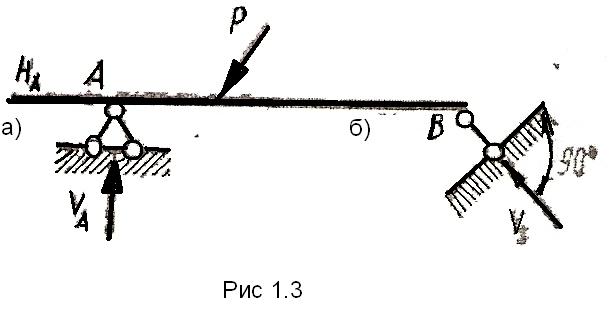 .
Шарнирно-неподвижная опора (рис 1.3а)
Реакция шарнирно-неподвижной опоры
проходит через центр шарнира, а её
величина и направление зависят от
действующих на тело нагрузок. Вместо
величины и направления этой реакции
целесообразно определять её составляющие
.
Шарнирно-неподвижная опора (рис 1.3а)
Реакция шарнирно-неподвижной опоры
проходит через центр шарнира, а её
величина и направление зависят от
действующих на тело нагрузок. Вместо
величины и направления этой реакции
целесообразно определять её составляющие
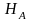 и
и
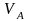
6. Шарнирно-подвижная опора (рис. 1.3б) реакция шарнирно подвижной опоры проходит через центр шарнира и перпендикулярна к опорной поверхности.
7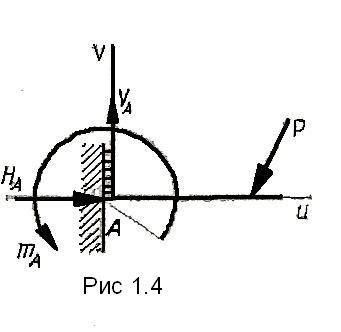 .
Заделка (защемление) показана на риc.
1.4. Такая опора (в плоской системе)
препятствует перемещению вдоль осей u
и v и не допускает поворота
защемленного сечения.
.
Заделка (защемление) показана на риc.
1.4. Такая опора (в плоской системе)
препятствует перемещению вдоль осей u
и v и не допускает поворота
защемленного сечения.
Разрешаемые методами статики задачи могут быть одного сечения из следующих типов:
8. Задачи, в которых известны ( полностью или частично) действующие на тело силы и требуется найти, в каком положении и при каких соотношениях между ними тело будет в равновесии.
9. Задачи, в которых известно, что тело заведомо находится в равновесии, и требуется найти чему равны при этом все или некоторые из действующих на тело сил.
Во
всех задачах статики реакции связей
относятся к числу неизвестных величин.
Задачи могут решаться аналитическим
или географическим методом. Выбор
системы координат и обозначений осей
хотя и произвольны, однако рациональный
выбор осей сможет упростить решение
задачи. В общем случае желательно, чтобы
возможно б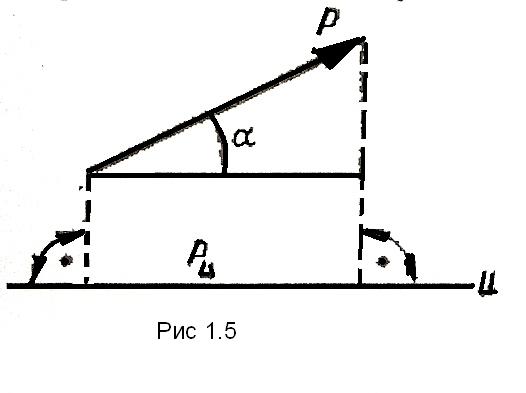 ольшее
число неизвестных сил было перпендикулярно
к той или иной координатной оси, тогда
уравнения равновесия получаются более
простыми.
ольшее
число неизвестных сил было перпендикулярно
к той или иной координатной оси, тогда
уравнения равновесия получаются более
простыми.
 Проекция силы Р
на ось u
(рис. 1.5)
Проекция силы Р
на ось u
(рис. 1.5)
 - величина скалярная. Проекция силы на
ось будет положительной, если угол между
направлением силы и положительным
направлением оси – острый, и отрицательной,
если этот угол – тупой.
- величина скалярная. Проекция силы на
ось будет положительной, если угол между
направлением силы и положительным
направлением оси – острый, и отрицательной,
если этот угол – тупой.
Если сила перпендикулярна к оси, то её проекция на ось равна нулю.
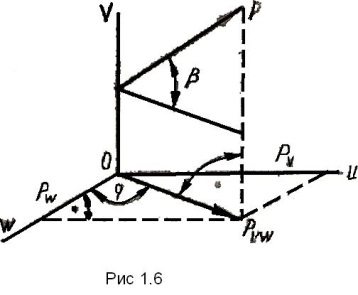
Проекция силы Р
на плоскость uOw
(рис 1.6)
 - величина векторная.
- величина векторная.
В некоторых случаях для нахождения проекции силы на ось бывает удобнее найти сначала её проекцию на плоскость, в которой эта ось лежит, а затем найденную проекцию на плоскость спроецировать на данную ось.
При составлении уравнений равновесия, в общем случае не имеет значения какое направление крутящего момента принять за положительное, однако с целью исключения различного толкования решений будем считать, что если момент стремится вращать тело вокруг некоторой точки по часовой стрелке он – отрицательный, если против часовой – положительный.
Обращаем внимание на правило вычисления момента силы относительно оси. Момент силы равен нулю, когда сила параллельна этой оси или пересекает её.
