5.2 По коаксиальным кабелям

 

При работе по коаксиальным кабелям всегда применяется однокабельная система.

 Тогда ожидаемая защищенность от собственных помех на входе регенератора  будет равна

 

А_{з ож}= Р_пер + 101 – 10lgF – 10lg(f_т/2) – 10lg h(Ац) ,                         (5.6)  

 

10lgh(Ац)=1,175·Ац – 20, дБ,

 

А_{з ож}= Р_пер + 121 – 10lgF – 10lg(f_т/2) – 1,175Ац  ,                            (5.7)  

 

Р_пер = 10lg(U²_пер · 10³/Z_в),                                                                            

U_пер = 3В,

Z_в – выбирается по таблице 12 приложения Б;

F – коэффициент шума корректирующего усилителя;

 

Ац=a(f_расч)^. ,

a(f_расч) - затухание кабеля на расчетной частоте, дБ/км рассчитано в разделе 1.2;

 - рассчитанная длина участка регенерации.

После выполнения расчетов необходимо сделать вывод о соотношении А_{з ож} и А_{З треб.}

 

 

Расчет требуемого числа уровней квантования

 

В ЦСП в результате квантования сигнала по уровню возникают ошибки, поскольку реальные мгновенные значения сигнала округляются до разрешенных уровней квантования. Эти ошибки, суммируясь с исходным сигналом, воспринимаются как флуктуационные шумы с равномерной спектральной плотностью.

В случае равномерного квантования, когда каждый шаг квантова­ния имеет величину  ∆U_p, мощность шума квантования в полосе частот канала ∆F равна

Р_шк = (∆U_Р ²/12)(2∆F /f_д),                                                (6.1)

 

где f_д - частота дискретизации сигнала.

Очевидно, чем меньше шаг квантования, тем меньше и мощность шумов квантования, но при этом число шагов квантования должно быть пропорционально больше, чтобы охватить весь динамический диапазон сигнала. Посколь­ку число шагов квантования связано с разрядностью кода, а следова­тельно, и со скоростью передачи, необходимо оценить, прежде всего, динамический диапазон квантуемого сигнала. Для этого воспользуемся экспериментально найденными статистическими законами распределения динамических уровней (волюмов) и мгновенных значений сигнала.

Известно, что плотность вероятности распределения волюмов соответствует гауссовскому закону распределения (см. рисунок 5.а)

 

W(y)=1/(σ_У√2π )× exp [-(y-y₀)²/2× σ_У],                           (6.2)

 

где у₀ – среднее значение волюма, дБ;

σ_У – его среднестатистическое отклонение, дБ.

График плотности распределения мощностей соответствующих динамическим уровням, показан на рисунке 5.б, его максимум соответствует волюму, но значение средней мощности очевидно, смещено вправо, поскольку мощности не принимают отрицательных значений. Из математической статистики известно, что уровень средней мощности может быть подсчитан по формуле

 

Р_ср = у₀+(ln 10/20) σ_y²=у₀+0,1151 σ_y²,                         (6.3)

 

а средняя мощность

Р_ср = 10^0,1р_ср, мВт

 

 

 

 

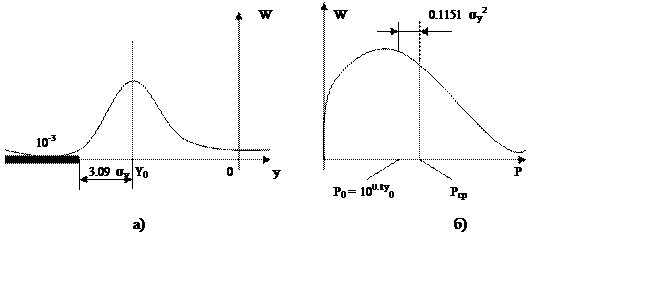
а) гауссовский закон; б) график плотности распределения мощностей, соответствующим динамическим уровням.

Рисунок 5 – Распределение вероятности волюмов

 

Мгновенные значения речевых сигналов распределены по закону, близкому к двустороннему экспоненциальному

3

W(u)=(α/2) exp (-α|u|), причем часто считают, что α≈√2/U_с, где U_с – эффективное значение сигнала (см. рисунок 6).

 

 

Рисунок 6 – Закон распределения мгновенных значений сигнала

 

Будем считать максимальное значение сигнала U_макс то, которое  может быть превышено с вероятностью, не более 10^-3.

Тогда    10^-3=0,5 exp (-α|U_макс|),       U_макс α≈√2/Uc = 4,933 U_c.

Q_пик = 20 lg (U_макс/U_c) = 10 lg (P_макс/Р_ср)=р_макс – р_ср

Таким образом, р_макс = р_ср+Q_пик,                                                          (6.4)

Согласно рекомендациям МСЭ-Т следует принимать P_макс для ЦСП равным +3 дБм0.

Заметим, что кодеры конструируют обычно так, что их напряжение ограничения соответствует максимальному напряжению сигнала, то есть

 

U_огр=U_макс= 0,7746×10^0.05Р_макс, В                                     (6.5)

 

Очевидно, что для волюмов, превышающих среднее значение, должны резко возрастать помехи из-за шумов ограничения. Однако здесь, видимо, сказывается психологический фактор – при слишком большой громкости, сопровождаемой искажениями, абоненты начинают говорить тише. При малых волюмах такая «саморегулировка» невозможна и поэтому расчет ведется для минимального сигнала, который соответствует минимальному напряжению минимального волюма. Минимальный волюм у_мин определяется как

 

У_мин = у_о – 3,09σ_у ,                                                 (6.6)

 

где 3,09 - аргумент интеграла вероятности, указывающий, что случай у<у_мин может наблюдаться с вероятностью ≤ 10^-3.Учитывая двусторонний экспоненциальный закон распределения (см. рисунок 6 левая часть) мгновенных значений сигнала (ведь и сигнал самого малого волюма должен быть обработан и передан с необходимо высоким качеством), получаем окончательно

 

р_мин = у_мин – Q_пик,                                         (6.7)

 

а с учетом (6.3),(6.4),(6.6) находим динамический диапазон сигнала

 

D_c = р_макс – р_мин = 2 Q_пик+3,09σ_у+0,115σ_у² .                           (6.8)

 

Величина шага квантования

                   

∆U_Р=2U_огр/N_кв,                                                      (6.9)

 

где N_кв – число шагов квантования, причем N_кв=2^m_Р;

m_p- число разрядов двоичного кода при равномерном квантовании.

Тогда минимальная защищенность от шумов квантования (для наименьших сигналов) с учетом псофометрического коэффициента К_П=0,75, полосы канала ТЧ ∆F=3,1 кГц и частоты дискретизации f_Д=8 кГц составит:

 

А_{з.кв.мин.}=10 lg [Р_мин/(Р_шкК_п²)]=10 lg

=10 lg (3/2) + 10 lg(f_Д/∆F)-20 lg К_П – D_с+m_p20 lg 2=6m_p-D_с+7,3, дБ. (6.10)

 

Порядок расчетов:

Максимальный и минимальный уровни сигнала:

 

Р_макс = y_O + 3s_У + Q_пик   ;                                      (6.11)

 

Р_мин = y_O - 3s_У ,                                                      (6.12)

 

где y_O - среднее значение сигнала,

     s_У - среднеквадратическое отклонение волюма сигнала.

Динамический диапазон сигнала

 

Д_с = Р_макс – P_мин   .                                                (6.13)

 

Минимальная защищенность от шумов квантования равна

 

А_{з.кв.мин} = = 6×m_p – D_с + 7,3.                                   (6.14)

 

Зная Д_с и А_{з.кв.мин} (см. исходные данные в таблице 2) находим число разрядов двоичного кода при равномерном квантовании

 

m_p = (А_{з.кв.мин} + Д_с - 7,3)/6.                                   (6.15)

 

Полученное значение округлить до целого числа.

Число уровней квантования  N_кв = 2 .  

Величина шага квантования при равномерном квантовании будет равна:

 

s_р = 2U_огр/N_кв ,                                                       (6.16)

 

где U_огр – напряжение ограничения.

 

U_огр = U_мах = 0,7746∙10^{0.05Pмакс} ;                           (6.17)

 

P_макс= +3дБм – по рекомендации МСЭ-Т для ЦСП.

 

U_огр = U_макс= 0.7746∙10^{0.05Pмакс} ,                           (6.18)

 

s_р = 2U_огр / N_кв  .                                                    (6.19)

 

Мощность шума квантования в полосе частот

P_ш.кв= s²_р /12.                                                        (6.20)

         

          Использование равномерного квантования не является оптимальным. В реальных системах ИКМ с временным разделением каналов используется неравномерное квантование, которое может быть осуществлено различными способами:

1)             сжатием динамического диапазона сигнала перед равномерным квантованием и последующим компенсирующим расширением его после линейного декодирования;

2)             непосредственно в кодирующем устройстве, т.е. путем применения нелинейного кодирующего устройства;

3)             с помощью соответствующего цифрового преобразования сигнала, формируемого на выходе линейного кодера, т.е. кодера с равномерной характеристикой (цифровое компандирование).

При неравномерном кодировании используются 8 мм разрядные коды, т.е. число уровней квантования равно 256.

При использовании нелинейного кодирования с характеристикой компадирования А 87,6/13 шаг квантования ∆U_н постоянен внутри каждого сегмента и увеличивается в 2 раза при переходе к каждому следующему сегменту, номер которого больше 1. В этом случае для 1-го сегмента можно записать:

∆U_н1 =   ∆U_н0;  при i=1а,1б;    2^i-1∆U_н0;   при i=2,…7.

При этом ∆U_н0 =2^-11 ∆U_огр.

В каждом сегменте размещается 16 шагов квантования (1-16, 17-32,…113-128).

Обозначим U_вх/U_огр = х. Учитывая, что 0 ≤ х ≤ 1, найдем х_н и х_в, - соответствующие нижней и верхней границам каждого сегмента (см. таблицу 6).

                           Таблица 6

№ сегмента	1а	1б	2	3	4	5	6	7
ХН	2-∞=0	2-7	2-6	2-5	2-4	2-3	2-2	2-1
ХВ	2-7	2-6	2-5	2-4	2-3	2-2	2-1	2-0 =0

 

Определим защищенность от шумов квантования в пределах i-ого сегмента. Границы сегментов при кодировании с характеристикой А87,6/13.

Для сегментов 1а, 1б

 

А_з.кв.i=10 lg[P_с/(P_шкК_п²)]= 10 lg{(U_огр х_i)²/[(∆U_н0 ²/12)(2∆FK_п²/f_д)]},             (6.30)

 

а с учетом равенства ∆U=2^-11U_огр, ∆F=3.1 кГц и К_п=0,75, имеем

 

А_з.кв.i=20 lg x_i+80.6, дБ.                                               (6.31)

 

Для сегментов с i = 2, 3…7:

 

A_{з кв.i}=20lg(х_i 2^12-i) + 14.4 дБ;                                          (6.32)

 

,                                                             (6.33)

где  = 3дБм.

Подставляя в (6.31) и (6.32) значения X_НI и  X_ВI , взятые из таблицы 6, можно оценить минимальное А'_з.кв и максимальное А"_з.кв - значения защищенности для начала и конца соответствующего сегмента характеристики. Данные расчета занести в таблицу 7.

 

Таблица 7

№сег	1а	1б	2	3	4	5	6	7
Аз кв (хн)
Аз кв (хв)
Р (хн)
Р (хв)

 

В сегментах 1а и 1б шаг квантования постоянен и равен  ∆U_н0. Таким образом, при любом уменьшении U_вх (х_i от значения 2^-6 ) будет пропорционально снижаться и А_з.кв  также, как и при равномерном квантовании.

Построить зависимости А_{з кв} х_н  = f (Р х_н ) и А_{з кв} х_в  = f (Р х_в ).